Итак, мы выяснили, что существует оптимальная сложность сети, зависящая от количества примеров, и даже получили оценку размеров скрытого слоя для двухслойных сетей. Однако в общем случае следует опираться не на грубые оценки а на более надежные механизмы адаптации сложности нейросетевых моделей к данным для каждой конкретной задачи. [c.66]
Первая попытка разработки нейросетевой модели прогнозирования конъюнктуры рын- [c.112]
| Рис.2.4.7. Кривая обучения нейросетевой модели прогнозирования недельного темпа | 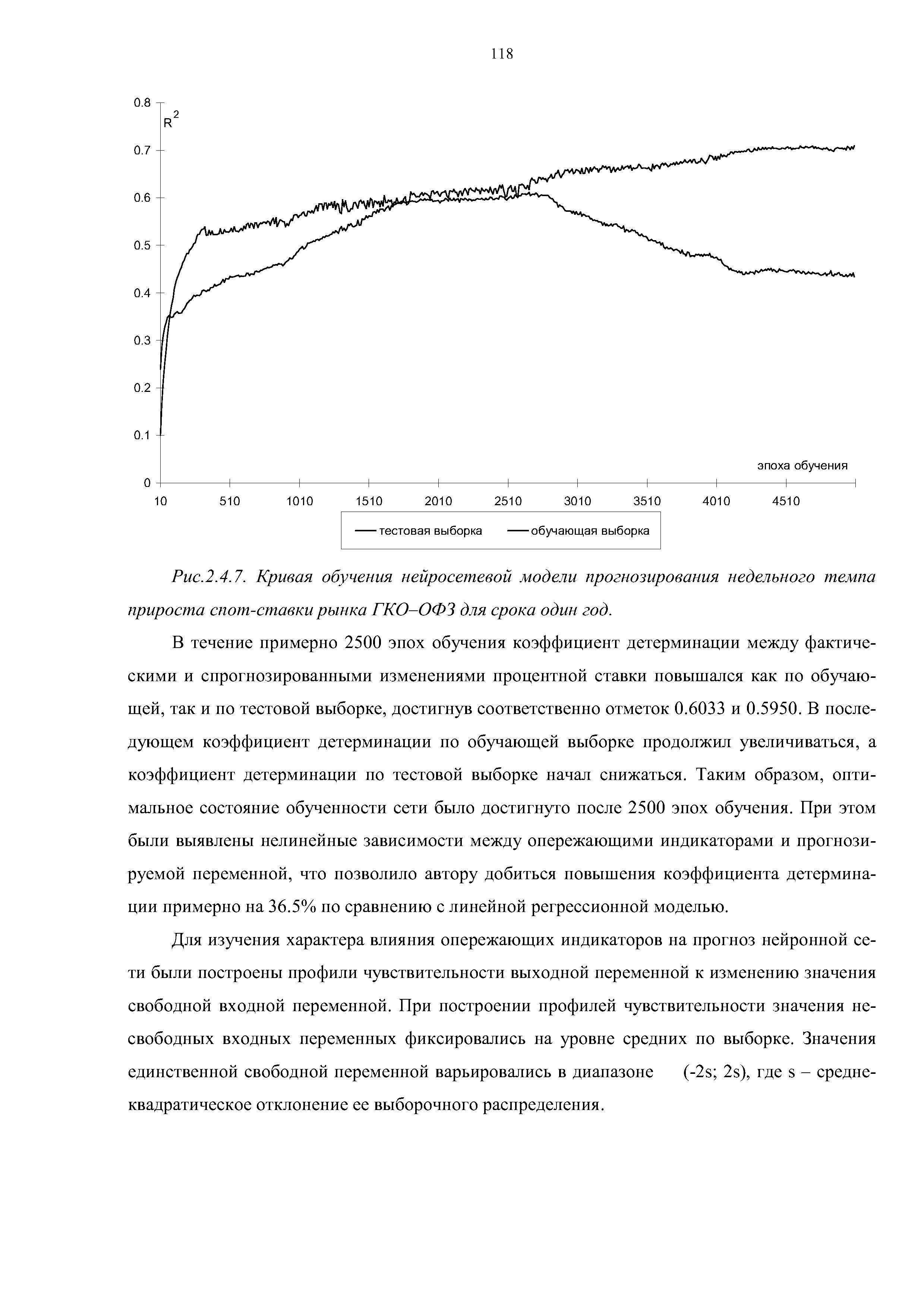 |
Гладков Э.А. Задачи прогнозирования качества и управления формированием шва в процессе сварки с использованием нейросетевых моделей // Сварочное производство, 1996. —№10. — С.36-Ч1. [c.340]
Выборка обучения для нейросетевой модели S = n,Y , представляющая собой множество пар векторов П и F, осуществляется с помощью достаточно хорошо апробированного ПВК оценки показателей надежности Орион [154]. Для этого ПВК дополнен блоком формирования (методами статистического моделирования) резервов мощности отдельных ЭЭС и пропускных способностей МСС объединения. Случайные изменения резервов мощности ЭЭС осуществляются в пределах оптимальных значений для условно изолированной системы и для всего объединения, при рассмотрении его как концентрированной ЭЭС (пропускные способности МСС не ограничены). Для каждого случайного состояния резервов мощности отдельных ЭЭС и пропускной способности МСС по ПВК Орион осуществляется расчет показателей надежности и их запись в специальный файл, необходимый для обучения нейросетевой модели. [c.157]
Итогом построения нейросетевой модели является функция Р(П), обеспечивающая наилучшую аппроксимацию G(ff) как на обучающем множестве S, так и на всей области ее определения. [c.158]
Оптимизация средств обеспечения надежности на базе нейросетевой модели. [c.158]
Время расчета оптимального варианта составляет доли секунды. В табл.2.6 приведено сопоставление результатов нейросетевой модели с результатами оптимизации, выполненной по ПВК Орион . Анализ табл.2.6 указывает на достаточно хорошее совпадение результатов. [c.160]
Применение нейросетевых моделей в большинстве случаев позволяет получить более достоверные результаты, так как дает возможность учитывать как достоверные и однозначно определяемые данные, так и неопределенные, мягкие (интенсивность рекламы организации и ее конкурентов, выплаты государственным служащим заработной платы, время года, изменения рыночных долей отраслевых организаций, динамику политической ситуации и т.д.) [c.241]
Нейросетевые модели состоят из входных, внутренних и выходных нейронов. Количество входных нейронов определяется количеством [c.241]
Данные модели допускают работу с нелинейными связями между параметрами, что дает им существенное преимущество перед линейными регрессионными моделями. На практике нейросетевые модели наиболее часто используются для прогнозирования перспективных объемов продаж, биржевых цен, обменных курсов, для выявления системных связей. [c.242]
В общем случае, чем за больший период удается собрать информацию, чем больше факторов учесть и адекватнее выбрать архитектуру нейросетевой модели, тем более достоверными оказываются прогнозы. [c.242]
Результат прогноза продаж количества телефонов сегмента 1 для 71-ой недели на основе нейросетевой модели равен 155 единиц продукции (рис. 3.8). [c.29]
Методы, описываемые в этой книге, относятся к общему классу нейросетевых моделей. Нейронные сети представляют собой совокупность математических методов, которые могут быть использованы для обработки сигналов, прогнозирования и кластеризации. Нейронные сети можно представить себе как нелинейные, многослойные и параллельные методы регрессии. Говоря проще, нейросетевое моделирование подобно проведению линии, плоскости или гиперплоскости через определенный набор информационных точек. Линию, плоскость или гиперплоскость можно с наилучшим приближением провести через любой набор данных и по выбору пользователя определить взаимосвязи, которые могут существовать между входами и выходами нейросети. Сеть можно также подстроить для представления многомерных данных в меньшей размерности. Существует два класса нейронных сетей сети, обучаемые с учителем и без учителя. [c.18]
Применение нейронных сетей для обработки экономических данных сопряжено с рядом трудностей. При использовании нейросетевых моделей в отдельных областях экономики (валютные рынки, рыночные индексы и т.п.) входные данные соотносятся с желаемыми выходными данными либо могут быть охарактеризованы с помощью ряда факторов. Это равносильно априорному предположению о существовании неких законов , управляющих преобразованием исходных временных рядов во множество выходных данных. Все это приводит к проблеме выявления репрезентативных рядов и факторов, существенных с точки зрения характеристики входных данных, а также значимых примеров. [c.159]
Если принять во внимание, что основными целями применения нейросетевых моделей являются кластеризация и визуализация данных, необходимо рассмотреть различные альтернативные подходы к визуализации и кластеризации. Существует несколько традиционных статистических методов кластеризации и визуализации данных (см. введение). Совмещение традиционных статистических методов с СОК может дать лучшие результаты, чем применение СОК самих по себе. Определить желаемую степень сжатия данных заранее также может оказаться полезным. [c.275]
Качество самообучающейся нейросетевой модели может и должно измеряться на основании (i) числа кластеров, (ii) качества кластеризации, (ш) устойчивости кластеризации (измеряемой сходством или отсутствием сходства, полученным при изменении множества тестовых данных). Если мы будем оценивать самообучающиеся нейросетевые модели подобным образом, мы, скорей всего, обнаружим, что между количеством, качеством и устойчивостью кластеров, полученных с помощью СОК, существует множество компромиссных вариантов. Поэтому наилучшая комбинация с точки зрения того или иного исследования должна определяться пользователем самостоятельно. В некоторых случаях требуемое сжатие данных может быть максимальным (минимальное число кластеров), и соответствующее низкое качество карты и слабая устойчивость будут вполне приемлемы для пользователя. В других случаях может потребоваться создание более тонко настроенной карты (т.е. карты с четкими границами между кластерами) и хорошая устойчивость без значительного сжатия данных. Например, при проведении макроэкономического анализа, анализа показателей мирового развития, качества окружающей среды, уровня бедности и в других подобных случаях требуется максимальное сжатие данных, поскольку соответствующие карты предназначаются для использования, главным образом, при определении политики и принятия решений на макроуровне. Для других задач, таких как картирование опционов и фьючерсных сделок, выбор фондовых управляющих, классификация клиентуры или продукции, анализ рынка, потребуется намного более тонкая дифференциация между кластерами. [c.283]
Помимо рассмотренной простейшей модели можно привести примеры других в некотором смысле эквивалентных моделей статистики и нейросетевых парадигм [c.202]
Способность работать с неточными данными является одним из главных достоинств нейронных сетей. Но она же парадоксальным образом является и их недостатком. Действительно, если данные не точны, то сеть в силу своей гибкости и адаптируемости будет подстраиваться к ним, ухудшая свои свойства обобщения. Эта ситуация особенно важна при работе с финансовыми данными. В последнем случае существует множество источников погрешности. Это и ошибки при вводе числовых значений или неправильная оценка времени действия ценных бумаг (например, они уже не продаются). Кроме того, если даже данные и введены правильно, они могут быть слабыми индикаторами основополагающих экономических процессов, таких как промышленное производство или занятость. Наконец, возможно, что многие важные параметры не учитываются при обучении сети, что эффективно может рассматриваться как введение дополнительного шума. Данные, далеко выпадающие из общей тенденции, забирают ресурсы нейронной сети. Некоторые из нейронов скрытого слоя могут настраиваться на них. При этом ресурсов для описания регулярных слабо зашумленных областей может и не хватить. Множество попыток применения нейронных сетей к решению финансовых задач выявило важное обстоятельство контроль гибкости нейросетевой модели является центральной проблемой. Изложим кратко существо процедуры обучения сети, объединенной с исправлением данных. Для простоты рассмотрим сеть с одним входом и одним выходом. В этом случае минимизируемой величиной является сумма двух слагаемых (Weigend Zimmermann, 1996) [c.177]
Заметим, что несмотря на неплохие, в общем-то, результаты, подобные нейросетевые модели весьма компактны. В качестве входных переменных обычно используется от 6 до 10 финансовых индикаторов, являющихся отношением наиболее значимых статей балансов и отчетов о прибылях и убытках корпораций. Например, в последней из упомянутых выше работ первоначально использовались 10 финансовых индикаторов, отобранных аналитиками одного из крупных американских банков. Однако по результатам анализа чувствительности нейросетевых предсказаний к входным переменным два из этих индикаторов оказались незначимыми и не использовались в окончательной модели (8-3-1 персептрон с 3 нейронами на скрытом слое и 1 выходным линейным нейроном, дающим численный эквивалент рейтинга). Качество воспроизведения "тонких" градаций (с учетом субкатегорий, например АА+, АА-) рейтинга агентства Standard Poor s, достигнутое этой моделью, иллюстрирует Рисунок 1. [c.185]
Нейросетевая модель оценки показателей надежности. Искусственные нейронные сети получили широкое применение как эффективный моделирующий аппарат. Это объясняется свойством нейронных сетей аппроксимировать и экстраполировать непрерывные вектор-функции, а также уникальным их свойством обобщения данных. Среди множест- [c.155]
Данная модель предполагает формирование Ключевых компетенций организаций, обеспечивающих реализацию программ Стратегического развития конкурентоспособности предприятия, и формирование профессиональных и поведенческих компетенций сотрудников и менеджеров на основе Образования, Совершенствования и Развития. Формируемые нами библиотеки базы знаний в виде инвариантных фреймов, понятий и рефрейминга основных компетенций и использование имитационной нейросетевой модели позволяют совместно с топ-менеджерами предприятий дополнить должностные инструкции руководителей и специалистов перечнем необходимых компетенций, обеспечивающих поддержку и развитие ключевых компетенций организации, необходимых для реализации программ повышения конкурентоспособности предприятия. [c.94]
Эти трудности могут быть частично преодолены введением гибкой нейронной структуры. Разработав гибридную нейросетевую модель, совмещающую обучающую процедуру метода СОК с эволюционной моделью, мы создали метод интегральной самоорганизации и генетики (ИСОГ). Сочетание СОК с генетическими алгоритмами может обеспечить получение более полной и осмысленной инфор- [c.159]
С каждым нейроном мы, таким образом, связываем модельный вектор ni(, т.е. координаты узла в пространстве сигналов представляются теперь в виде соответствующего нейрону множества вещественных чисел. В обычных нейросетевых моделях модельный вектор соответствовал бы синаптическим весам, однако в нашем случае конкретизировать природу ni( нет необходимости. [c.228]
Без надлежащего определения целей разработки нейросетевой модели, обучаемой с учителем или без учителя, оценить эффективность полученных на выходе результатов будет трудно. Нейросетевые модели можно строить для решения множест- [c.274]
Статистика ошибок. Следующая немаловажная разработка сетевых решений заключается в определении того, что использовать в качестве статистики ошибок (отклонений) для апробации и для тестирования. Мерой измерения ошибок (отклонений) может служить разность между точно вычисленным каким-то статистическим значением ошибок, например их скользящей средней, и выходными данными нейросети. Эта разность должна быть определена для каждого из событий в тестовом множестве, просуммирована и затем разделена на число событий в тесте. Это стандартная мера ошибок, которая называется средней ошибкой . Другие способы вычисления ошибки включают в себя среднее значение абсолютных ошибок, сумму квадратов ошибок или же квадратный корень ошибок (Root-mean-squared — RMS). После того как будет выбрана нейросетевая модель, ее следует апробировать еще раз на определенных временных промежутках. Следующий этап исследования должен заключаться в модификации вхо- [c.134]
Не следует, однако, обольщаться существованием столь простого рецепта определения значимости входов. Линейная модель может быть легко построена и без привлечения нейросетей. Реальная сила нейроанализа как раз и состоит в возможности находить более сложные нелинейные зависимости. Более того, для облегчения собственно нелинейного анализа рекомендуется заранее освободиться от тривиальных линейных зависимостей - т.е. в качестве выходов при обучении подавать разность между выходными значениями и их линейным приближением. Это увеличит "разрешающую способность" нейросетевого моделирования (см. Рисунок 12). [c.140]
До сих пор нейросети рассматривались нами лишь как инструмент предсказания, но не понимания. Действительно, классический нейросетевой подход - метод черного ящика -предполагает создание имитационной модели, без явной формулировки правил принятия решений нейросетью. Вернее, эти правила содержатся в весах обученной нейросети но понять их, переформулировав на язык "если. .. -то. .." не представлялось возможным. Бэтой главе мы продемонстрируем методику, позволяющую строить подобные правила, объясняющие нейросетевые решения. Нейросети, таким образом, можно использовать не только для предсказаний, но и для извлечения знаний из баз данных. [c.167]
Поскольку в настоящее время нейронные сети с успехом используются для анализа данных, уместно сопоставить их со старыми хорошо разработанными статистическими методами. В литературе по статистике иногда можно встретить утверждение, что наиболее часто применяемые нейросетевые подходы являются ни чем иным, как неэффективными регрессионными и дискриминантными моделями. Мы уже отмечали прежде, что многослойные нейронные сети действительно могут решать задачи типа регрессии и классификации. Однако, во-первых, обработка данных нейронными сетями носит значительно более многообразный характер - вспомним, например, активную классификацию сетями Хопфилда или карты признаков Кохонена, не имеющие статистических аналогов. Во-вторых, многие исследования, касающиеся применения нейросетей в финансах и бизнесе, выявили их преимущества перед ранее разработанными статистическими методами. Рассмотрим подробнее результаты сравнения методов нейросетей и математической статистики. [c.198]
Еще одним существенным различием является то. что для методов статистики не имеет значения, каким образам будет минимизироваться невязка - в любом случае модель остается той же самой, в то время как для нейрокомпьютинга главную роль играет именно метод обучения. Иными словам и. в отличие от нейросетевого подхода оценка параметров модели для статистических методов не зависит от метода минимизации. В то же время статистики будут рассматривать изменения вида невяэки скажем на [c.201]
В отличие от нейросетевого подхода в котором основное время забирает обучение сетей при статистическом подходе это время тратится на тщательный анализ задачи. При этом опыт статистиков используется для выбора модели на основе анализа данных и информации, специфичной для данной области. Использование нейронных сетей - этих универсальных аппроксиматоров - обычно проводится без использования априорных знаний, хотя в ряде случаев оно весьма полезно. Например для рассматриваемой линейной модели использование именно среднеквадратичной ошибки ведет к получению оптимальной оценки ее параметров, когда величина шума имеет нормальное распределение с одинаковой дисперсией для всех обучающих пар. В то же время если известно, что эти дисперсии различны, то использование взвешенной функции ошибки [c.201]
