Постройте регрессионные модели (линейную, гиперболу, экспоненту, параболу) для следующих исходных данных (табл. 9.4). Для облегчения расчетов исходные данные содержат только четыре пары значений (х , yj). [c.122]
Математические модели корреляционного анализа в форме коэффициентов имеют ограниченные аналитические возможности. Зная лишь направление ковариации показателей и тесноту связи, невозможно определить закономерности формирования уровня результативного показателя под влиянием исследуемых факторов, оценить интенсивность их влияния, классифицировать факторы на основные и второстепенные. Для этих целей используются модели регрессионного анализа. Линейная модель (уравнение) регрессионного анализа может быть представлена в виде [c.282]
Рассмотрим теперь задачу 1 из заданий по анализу регрессии, приведенную на с. 300—301. Построим линейную регрессионную модель по методу наименьших квадратов. Обозначим через f, год выпуска автомобилей, а через Л/. — объем выпуска в этом году. Данные, представленные в таблице, изобразим на графике, представленном ниже. [c.283]
Значимость коэффициентов простой линейной регрессии (а и Ь) также может быть установлена с помощью /-критерия Стьюдента. Кроме того, адекватность однофакторной регрессионной модели можно оценить с помощью F-критерия Фишера, алгоритм которого выглядит таким образом [c.76]
Зависимости в экономике могут быть не только прямыми, но и обратными, и нелинейными. Регрессионная модель может быть построена при налички любой зависимости, однако в многофакторном анализе чаще всего используют линейные модели вида. [c.122]
В главах 3,4 рассмотрены классические линейные регрессионные модели в главе 3 — парные регрессионные модели, на примере которых наиболее доступно и наглядно удается проследить базовые понятия регрессионного анализа, выяснить основные предпосылки классической модели, дать оценку ее параметров и геометрическую интерпретацию в главе 4 — обобщение [c.3]
Линейная регрессионная модель [c.17]
Вторая причина, по которой линейная регрессионная модель оказывается предпочтительнее других, — это меньший риск значительной ошибки прогноза. [c.18]
В настоящем учебнике мы в основном будем рассматривать линейные регрессионные модели, и, по мнению авторов, это вполне соответствует той роли, которую играют линейные модели в эконометрике. [c.19]
Наиболее хорошо изучены линейные регрессионные модели, удовлетворяющие условиям (1.6), (1.7) и свойству постоянства дисперсии ошибок регрессии, — они называются классическими моделями. [c.19]
B случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, т. е. R2 = r2. Действительно, учитывая (3.12), (3.17), [c.75]
В предыдущих главах была изучена классическая линейная модель регрессии, приведена оценка параметров модели и проверка статистических гипотез о регрессии. Однако мы не касались некоторых проблем, связанных с практическим использованием модели множественной регрессии. К их числу относятся мультиколлинеарность, ее причины и методы устранения использование фиктивных переменных при включении в регрессионную модель качественных объясняющих переменных, линеаризация модели, вопросы частной корреляции между переменными. Изучению указанных проблем посвящена данная глава. [c.108]
При функциональной форме мультиколлинеарности по крайней мере одна из парных связей между объясняющими переменными является линейной функциональной зависимостью. В этом случае матрица Х Х особенная, так как содержит линейно зависимые векторы-столбцы и ее определитель равен нулю, т. е. нарушается предпосылка 6 регрессионного анализа. Это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели. [c.108]
Линейные регрессионные модели с переменной структурой. Фиктивные переменные [c.115]
Качественные признаки могут существенно влиять на структуру линейных связей между переменными и приводить к скачкообразному изменению параметров регрессионной модели. В этом случае говорят об исследовании регрессионных моделей с переменной структурой или построении регрессионных моделей по неоднородным данным. [c.116]
Построить линейную регрессионную модель Y по X с использованием фиктивной переменной по фактору пол . Можно ли считать, эта модель одна и та же для юношей и девушек [c.119]
В критерии (тесте) Г. Чоу эти трудности в существенной степени преодолеваются. По каждой выборке строятся две линейные регрессионные модели [c.123]
До сих пор мы рассматривали линейные регрессионные модели, в которых переменные имели первую степень (модели, линейные по переменным), а параметры выступали в виде коэффициентов при этих переменных (модели, линейные по параметрам). Однако соотношение между социально-экономическими явлениями и процессами далеко не всегда можно выразить линейными функциями, так как при этом могут возникать неоправданно большие ошибки. [c.124]
Вопрос об эффективности линейной несмещенной оценки вектора р для обобщенной регрессионной модели решается с помощью следующей теоремы. [c.152]
Регрессионные модели не линейные по параметрам 125, 126 -------переменным 125 [c.304]
Регрессионный анализ - один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, х[,х2,...,хп у должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида [c.101]
Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар А в зависимости от дохода необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям, т.е. Лу = f (Лх), если ряды динамики характеризуются линейной тенденцией. [c.145]
Для линейной зависимости признаков скорректированный коэффициент множественной корреляции определяется по той же формуле, что и индекс множественной корреляции, т.е. как корень квадратный из R2. Отличие состоит лишь в том, что в линейной зависимости под т подразумевается число факторов, включенных в регрессионную модель, а в криволинейной зависимости т — число параметров при х и их преобразованиях (х2, In х и др.), которое может быть больше числа факторов как экономических переменных. Так, если у -f(xb x-J, то для линейной регрессии т = 2, а для регрессии вида [c.120]
На втором этапе анализа следует проверить гипотезу, которая будет выдвинута на первом этапе, путем построения регрессионных моделей. Кривые жизненного цикла товаров (ЖЦТ), предприятий, отраслей в конкретных случаях могут существен- но различаться, поэтому подбор математической модели — функции, описывающей жизненный цикл в целом, как правило, затруднителен. В связи с этим каждый из четырех этапов жизненного цикла анализируют отдельно. Используются линейные модели, а также модели полиномов второй и третьей степени [c.91]
| Рис. 4.3. Графики линейных регрессионных моделей выручки от реализации | 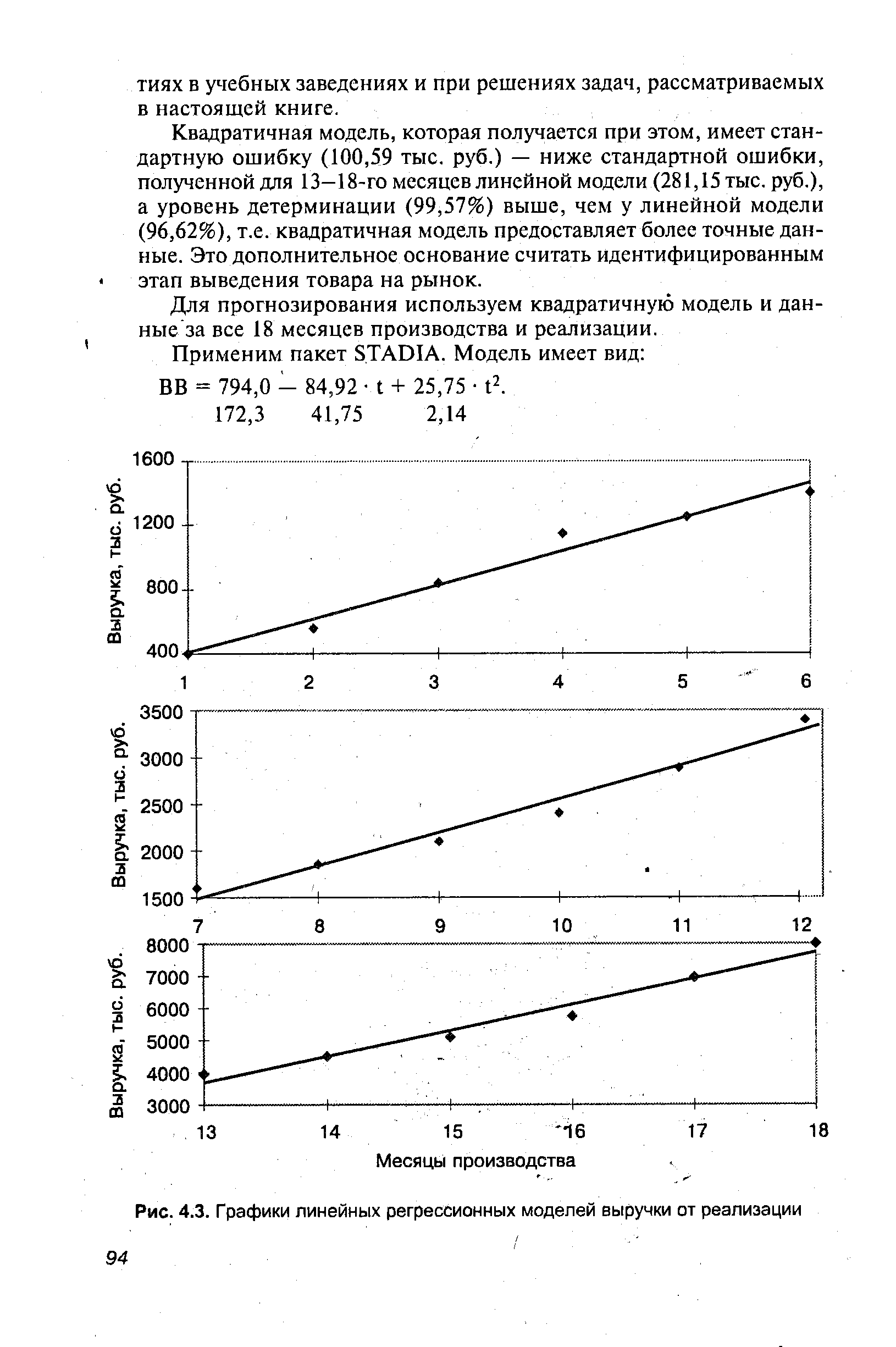 |
| Рис. 2.3. Графики линейных регрессионных моделей выручки | 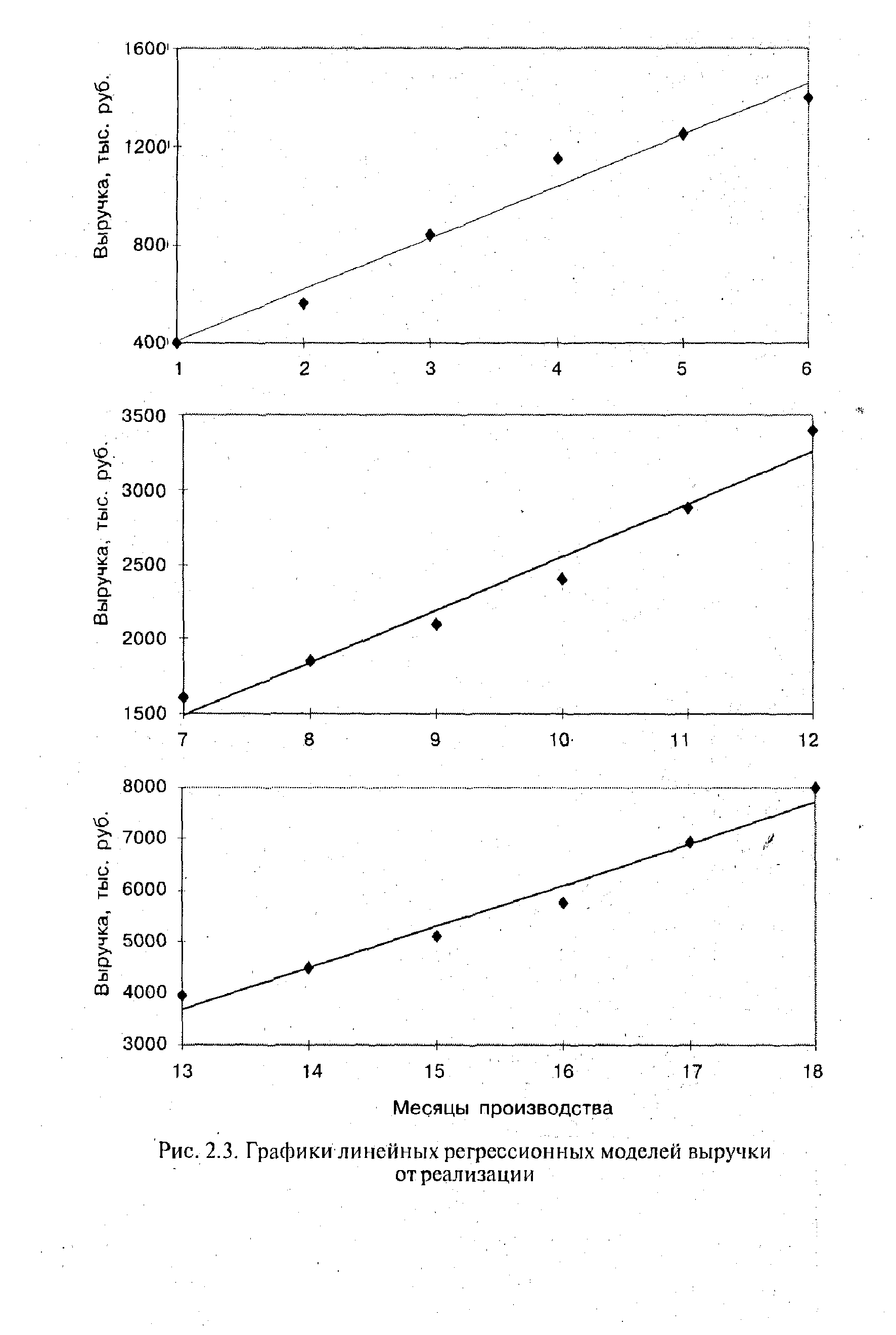 |
Теорема Айткена. В классе линейных несмещенных оценок вектора р для обобщенной регрессионной модели оценка [c.152]
Как уже отмечалось выше, равенство дисперсий возмущений (ошибок) регрессиии е/ (гомоскедастичность) является существенным условием линейной классической регрессионной модели множественной регрессии, записываемым в виде У е [c.155]
Пример 7.1. По данным л = 150 наблюдений о доходе индивидуума Y (рис. 7.2), уровне его образования Х и возрасте Xi выяснить, можно ли считать на уровне значимости а=0,05 линейную регрессионную модель У по Х и Х- гетероскедастичной. [c.160]
Применяя к линейной регрессионной модели (7.25) теорему Айткена ( 7.2), наиболее эффективной оценкой вектора р является оценка (7.7) [c.164]
РЕГРЕССИОННАЯ МОДЕЛЬ [regression model] — экономико-статистическая модель, основанная на уравнении регрессии, или системе регрессионных уравнений, связывающих величины экзогенных (входных, "объясняющих") и эндогенных (выходных) переменных. Примеры см. в ст. "Линейная модель", "Регрессионный анализ". [c.304]
ЭКОНОМЕТРИЧЕСКАЯ МОДЕЛЬ [e onometri model] — основное понятие эконометрии, экономико-математическая модель, параметры которой оцениваются с помощью методов математической статистики. Она выступает в качестве средства анализа и прогнозирования конкретных экономических процессов как на макро-, так и на микроэкономическом уровне на основе реальной статистической информации. Наиболее распространены Э.м., представляющие собой системы регрессионных уравнений, в которых отражается зависимость эндогенных величин (искомых) от внешних воздействий (текущих экзогенных величин) в условиях, описываемых параметрами модели, а также лаговыми переменными (см. Лаг). Кроме регрессионных (как линейных, так и нелинейных) уравнений, применяются и другие матема-тико-статистические модели. [c.400]
Смотреть страницы где упоминается термин Регрессионная модель линейная
: [c.574] [c.20] [c.60] [c.61] [c.62] [c.152] [c.967] [c.120] [c.118] [c.119] [c.130] [c.55] [c.301]Эконометрика начальный курс (2004) -- [ c.39 ]
