| Таблица 23. Матрица прямых затрат и выпуска продукции по |  |
| Таблица 9. Матрица прямых затрат в модели оптимальной | 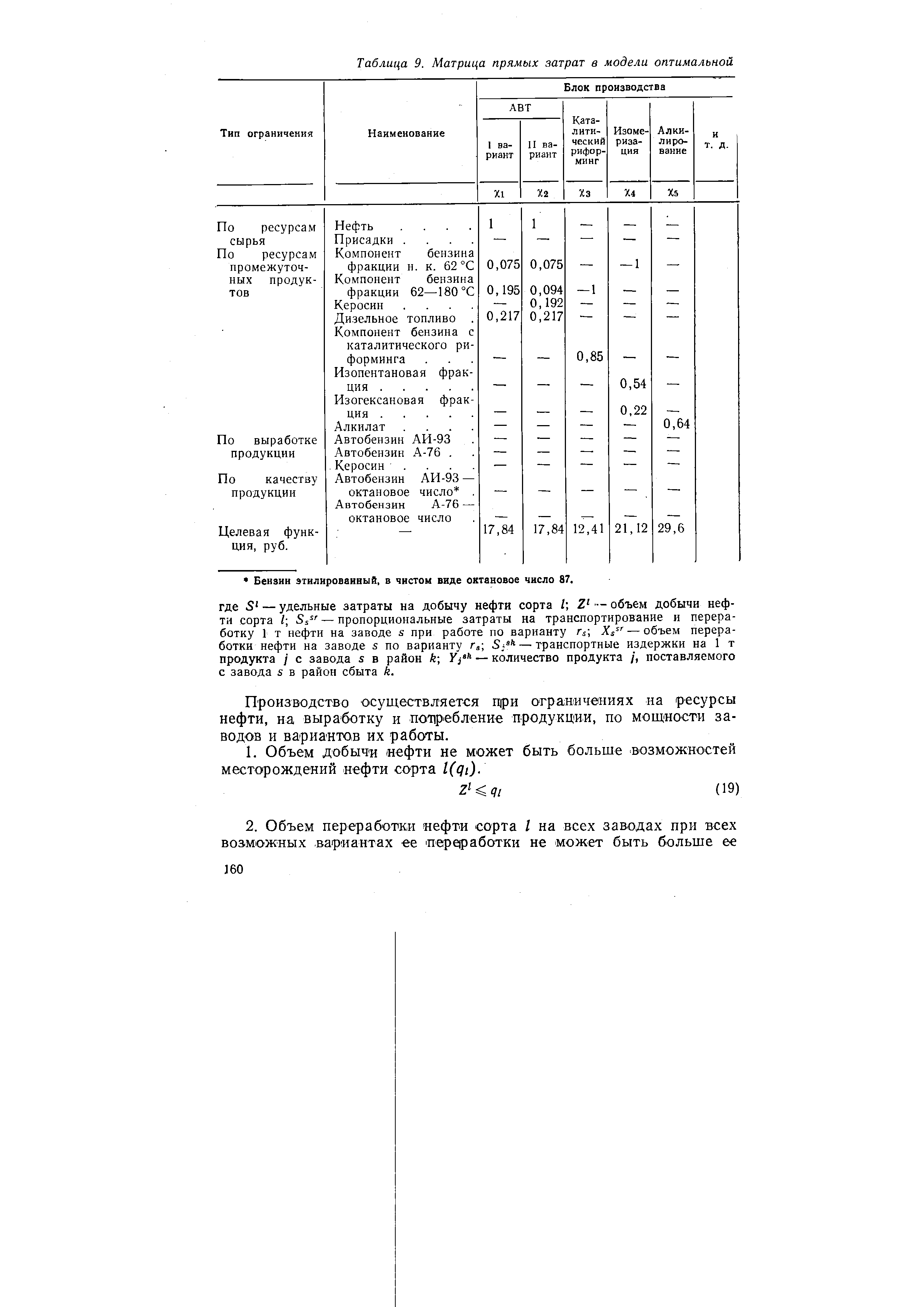 |
Таким образом, (Е-А)В-Е, т. е. В = (Е — А) 1. Итак, обратная матрица (Е — А 1 существует и представима в виде (2.8ч Из (2.8) следует, что все элементы матрицы (Е — А) 1 неотрицательны, а некоторые положительны. Таким образом, для любого неотрицательного вектора конечного продукта у существует неотрицательный вектор валовых выпусков х, удовлетворяющий соотношению (2.3). В этом случае матрицу прямых затрат А принято называть продуктивной ). [c.266]
Вопрос о продуктивности матрицы прямых затрат в случае рассматриваемого нами межотраслевого баланса в стоимостном (денежном) выражении решается проверкой достаточного условия продуктивности (2.6). При использовании других форм межотраслевого баланса этот вопрос оказывается более сложным (см. [29]). [c.266]
Точнее говоря, матрица прямых затрат А называется продуктивной, если существует такой неотрицательный вектор х°, что (Е — А)х° > 0. Поскольку для этого необходимо и достаточно, чтобы (Е — 4) 5гО, то неотрицательность матрицы В = (Е — А)"1 также может браться в качестве определения продуктивности матрицы прямых затрат. [c.266]
Элементы матрицы прямых затрат А представляют собой коэффициенты прямых затрат продукции /-го вида на производство единицы продукции у-го вида. В нашем примере эти коэффициенты будут такими [c.182]
I квадрант матрицы разбивается на четыре подматрицы. Матрица А представляет собой нормативную матрицу прямых затрат, отражающих непосредственно расход одного продукта на производство другого. [c.228]
Нормативная матрица прямых затрат [c.231]
AI = (ai)nm матрица прямых затрат (матрица А в первоначальной модели межотраслевого баланса, которая имеет вид [c.237]
Прокомментируйте следующую матрицу прямых затрат (руб.) [c.112]
Вектор х называется вектором валового выпуска, вектор у называется вектором конечного потребления, а матрица А — матрицей прямых затрат. Соотношение (1.3) называется уравнением линейного межотраслевого баланса. Вместе с изложенной интерпретацией матрицы А и векторов х и у это соотношение называют также моделью Леонтьева. [c.256]
У — величина внутреннего конечного продукта региона ",, — коэффициенты матрицы прямых затрат межотраслевого балан- [c.317]
Правильно ли следующее утверждение Если коэффициенты матрицы прямых затрат увеличить в два раза, то компоненты вектора оптимального решения в задаче на максимум дохода уменьшатся в два раза . [c.46]
Вектор-столбец г затрат внешних ресурсов связан с валовым продуктом соотношением г = Су, где С = (Сц)т п — матрица прямых затрат ресурсов. Равенство (4) позволяет непосредственно связать потребное количество внешних ресурсов с конечным продуктом г = СВх, или г = Dx, где матрица D = СВ связывает затраты внешних ресурсов с конечным продуктом. Используя обозначение R для вектора располагаемых ресурсов, приходим к явному описанию множества производственных возможностей [c.679]
Есть два основных способа решения этой задачи. Первый — подсчет косвенных затрат и их прибавление к прямым. Второй — непосредственное получение коэффициентов полных затрат из матрицы прямых затрат — с помощью операции, называемой обращением матрицы. В последнем случае решение системы балансовых уравнений приводит к матрице (таблице) коэффициентов полных затрат [c.78]
Выражение в скобках обозначает здесь разность между единичной матрицей Е, у которой по главной диагонали — единицы, а остальные элементы — нули, и матрицей прямых затрат. (Единичная матрица часто обозначается не буквой Е, а буквой ( ). [c.78]
НУЛЕВЫЕ ЭЛЕМЕНТЫ МАТРИЦЫ. В матрице прямых затрат межотраслевого баланса они означают, что между соответствующими отраслями, представленными в строке и столбце, пересекающихся в данной ячейке, нет никаких хозяйственных связей (или они признаются пренебрежимо малыми и сводятся к нулю, чтобы сократить расчеты). [c.82]
Нормативная матрица прямых затрат по плану материально-технического снабжения Собинского АТП для маршрутных автобусов приведена в табл. 3. [c.20]
Имея выведенную за ряд лет нормативную матрицу прямых затрат по материально-техническому снабжению, нетрудно было определить общий план материально-технического снабжения маршрутных автобусов Собинского АТП на заданную производственную [c.21]
| Таблица 7. Матрица прямых затрат в модели | 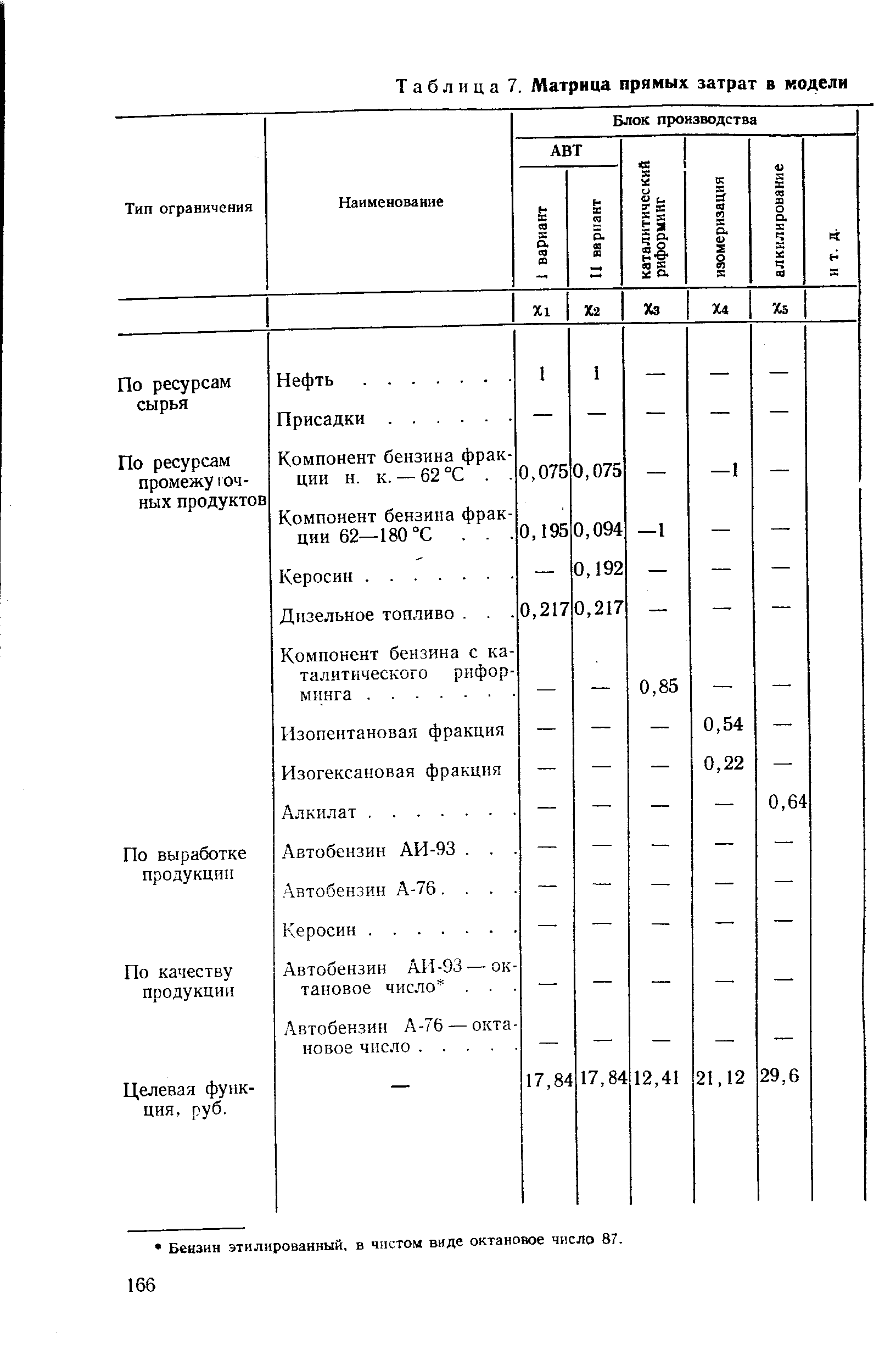 |
Простейшая динамическая модель макроэкономики. Представим экономику некоторого региона как совокупность п отраслей (/ е 1 п), валовой продукт которых в денежном выражении на некоторый момент t может быть представлен в виде вектора г1 = ( , 4 > где еО (Г-1). Обозначим через А матрицу прямых затрат, элементы которой я- у отражают затраты продукции /-и отрасли (в денежном выражении) на изготовление единицы продукции /-и отрасли в t-й момент времени. Если = U-, — матрица, задающая удельные нормы про- [c.201]
Построить матрицу прямых, полных и косвенных затрат 2-го порядка. 13. Дана матрица прямых затрат [c.11]
А1 - матрица коэффициентов косвенных затрат 1-го порядка. 15. Дана матрица прямых затрат [c.12]
Найти матрицу прямых затрат и построить модель Леонтьева. [c.12]
Определение 2. Матрица А называется матрицей прямых затрат, а [c.15]
По заданной матрице прямых затрат и вектору конечной продукции, установить продуктивность матрицы прямых затрат, определить коэффициенты полных затрат. [c.18]
Матричная модель техпромфинплана включает в себя нормативные матрицы удельных норм прямых затрат материалов, энергии, труда и денежных средств на единицу продукции матрицу полных затрат всех видов матрицы производственной программы и производственной мощности матрицу себестоимости и др. [c.73]
Коэффициенты прямых затрат образуют квадрантную матрицу А (а/у), содержащую п строк и п столбцов. [c.159]
Целевая функция и система ограничений могут быть представлены в виде исходной матрицы прямых затрат.. Примерная ее форма показана в табл. 9. Для решения описанной задачи современные ЭВМ имеют стандартные программы. Преимущество такой модели е только в том, что она показывает наиболее рациональную технологическую схему, необходимую производственную мощность каждой из технологических установок, рациональное использование промежуточных продуктов при минимуме приведенных затрат, но и в том, что, пользуясь ею, можно определить, как изменится критерий оптимальности, если один из ограиичен- [c.158]
Межотраслевые связи, представленные в межотраслевом балансе, могут быть выражены в виде экономико-математической модели. Ядром модели является матрица прямых затрат, элементы которой представляют собой нормы расхода продукции одних отраслей народного хозяйства на единицу продукции других отраслей. Если вало вую продукцию отрасли-поставщика обозначить А , валовую продукцию отрасли-потребителя — Xj, а затраты продукции i-й отрасли на производство продукции у -й отрасли — Х , то коэффициент прямых затрат о, оудет равен Xjj/X,. Матрица А=//а, //, состоящая из этих коэффициентов, характеризует структуру межотраслевых связей в народном хозяйстве. С ее помощью может быть записано основное уравнение межотраслевого баланса — уравнение распределения продукции [c.440]
Применение математических методов расчета техпромфинпла-на требует формирования плановых нормативных матриц прямых затрат, которые составляются раздельно для основного и вспомогательного производств. [c.115]
Целевая функция и система ограничений МОГУТ бьпь представлены и ни.к- исходной матрицы прямых затрат. Примерная ее форма показана в табл. 7. Для решения описанной задачи современные ЭВМ имеют стандартные программы. Преимущество такой модели не только в том, что она показывает наиболее рациональную технологическую схему, необходимую производственную мощность каждой из технологических установок, рациональное использование промежуточных продуктов при минимуме приведенных затрат, но и в том, что на ее основе известно, как изменится критерий оптимальности, если один из ограниченных ресурсов увеличится на единицу, т. е. получается оценка ресурса. Эти оценки получаются в целевой строке симплексной таблицы. ОднакЪ следует учитывать ограниченность этих оценок. Они целиком и полностью зависят от исходных условий, т. е. действуют в определенном пределе. Стандартные программы дают возможность при однократном решении рассчитать устойчивость этих оценок. [c.165]
Примером показателей прямых затрат являются К. п. з. ftjj продукции отрасли i (продукции, включаемой в г -ю позицию классификатора продукции) на единицу продукции /-и отрасли (или /-и позиции номенклатуры продуктов), используемые при анализе отчётных и составлении плановых межотраслевых балансов в стоимостном и натуральном выражениях (см. Баланс межотраслевой). Для межотраслевого баланса произ-ва и распределения продукции га отраслей материального произ-ва совокупность п показателей прямых затрат a/j (ij = 1,. .., п) образует матрицу прямых затрат (а), т. е. таблицу из га строк и п столбцов, в каждой из клеток к-рой записывается соответствующая величина прямых затрат ац. [c.277]
Применение межотраслевого баланса для целей долгосрочного прогнозирования ставит перед исследователем ряд беспрецедентных по своей сложности инфор-мационно-технич. задач. Гл. из них — прогноз коэффициентов матриц прямых затрат, к-рый может быть получен только на основе анализа динамики воспроизводств. структуры всей экономики. Такого рода анализ может базироваться только на фиксированной информации о структурных сдвигах, в частности о тех, к-рые обусловлены внедрением новых технологий. Даже при высоком уровне агрегирования коэффициенты прямых затрат будут существенно зависеть от изменения доли электростали в нроиз-ве электроэнергии и т. п. Т. о., экзогенное (внемоделыюе) задание матрицы коэффициентов прямых затрат на отдалённую перспективу равносильно принятию многочисленных предположений относительно будущей структуры нар. х-ва. Для предсказания п значений объёмов отраслевых продуктов в прогнозируемом году необходимо, по. меньшей мере, п(п -f 1) величин спрогнозировать экзогенно. При этом ограничения относительно структур модели могут оказаться столь серьёзными, что не будет оснований для положительного ответа на вопрос о принципиальной реализуемости полученного варианта матрицы. В связи с этим следует обратить внимание на особую детализацию разработки в глобальном проекте Будущее мировой экономики целого ряда вариантов расчётов при неизменной матрице прямых затрат. Поскольку модель, межотраслевых связен строится для каждого из 15 рассматриваемых Леонтьевым регионов, приходится задавать матрицы прямых затрат и для тех из них, для к-рых соответств. исходной информации не существует. Поэтому авторы проекта широко пользовались прогнозом коэффициентов на основе их регрессионной зависимости от душевого уровня валового нац. продукта (количество наблюдений не превышало восьми). Если [c.616]
Модель Леонтьева — квазидинамическая, т. е. она сразу выходит на конечный год периода прогноза, но допускает получение промежуточных значений, если известна динамика коэффициентов матрицы прямых затрат и факторы, определяющие вектор конечного спроса для каждого региона. Чтобы оценить платёжный баланс рассматриваемых в модели регионов, необходимо ввести в неё цены мирового рынка для года прогноза. Эти цены определяются на основе двойственных оценок баланса североамер. региона. На первый взгляд, распространение на весь мировой рынок оценок продукции, свойственных наиболее развитому в технологич. отношении региону, создаёт остальным участникам междунар. разделения труда благоприятные условия для обмена. Это связано с тем, что большие оценки получает продукция, менее доступная для произ-ва внутри этого региона (т. е. сырьё, полуфабрикаты, трудоёмкие виды продукции), а товары, требующие более развитой технологии, оцениваются менее высоко по сравнению с теми оценками, к-рые они получили бы при произ-ве в др. регионах. Подобная гипотеза расходится с реальным положением в мировой торговле, ибо цены на технологии и оборудование испытывают постоянную тенденцию к опережающему росту. Помимо этого они сразу же, т. е. в момент появления на рынке технологии, нового продукта или оборудования, устанавливаются в соответствии с эффектом, достигаемым при использовании этих товаров, а в дальнейшем могут расти не обязательно опережающим темпом, если доля новых товаров и товаров, произведённых посредством новых технологий, в продукции и экспорте развитой страны высока. След., сравнение движения официальных индексов цен из-за различных принципов формирования базы не отражает истинной динамики соответств. нар.-хоз. оценок, скрывая значит, часть инфляции в развитых капиталпстич. странах и более явственно обнажая её в странах развивающихся, экономика к-рых менее мобильна. [c.616]
Смотреть страницы где упоминается термин Матрица прямых затрат
: [c.135] [c.264] [c.270] [c.241] [c.679] [c.175] [c.293] [c.163] [c.424] [c.12] [c.22]Введение в экономико-математическое моделирование (1984) -- [ c.264 ]
