При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение и получения возможности сравнивать частоты. [c.32]
Построение гистограммы распределения. [c.81]
После построения гистограммы распределения можно выдвинуть гипотезу о том, что данная гистограмма может быть аппроксимирована одним из изученных ранее законов распределения. При этом степень близости гистограммы и принятой аналитической модели может быть проверена с использованием критериев согласия. Здесь будет рассмотрен один из этих критериев - критерий Пирсона. [c.87]
Построение гистограмм распределений факторов [c.57]
О выполнять статистическую обработку данных (построение рядов, гистограмм распределения, графиков сглаживания и т. п.) [c.472]
Проверка правильности выдвинутых гипотез о закономерностях распределения времени пролеживания предметов труда на межцеховых складах осуществлена методом выравнивания эмпирических интервальных рядов распределения. С этой целью по предварительным результатам графического анализа построенных гистограмм были подобраны теоретические кривые плотности распределения, которые представ лены следующими функциями показательной, закона [c.77]
Подробно рассмотрена проблема группировки данных, то есть расчет оптимального количества интервалов группировки и оптимальной ширины интервала, а также построения по сгруппированным данным гистограммы распределения. [c.79]
Таким образом, задача выбора оптимального числа интервалов при построении гистограммы — это задача оптимальной фильтрации, а оптимальным числом интервалов является такое, когда максимально возможное сглаживание случайных флуктуации данных сочетается с минимальным искажением от сглаживания самой кривой искомого распределения. [c.37]
Оценка методом Монте-Карло произведена с использованием тех же исходных параметров, меняющихся в тех же диапазонах, однако сами параметры задавались в виде функций логнормального распределения со средним значением, равным базовому, и логарифмической дисперсией 0,1 (рис. 13.5). Затем при помощи компьютера производилось генерирование случайных значений этих функций и их случайных комбинаций в сценарии. Общее количество полученных сценариев составило около 5000. Для каждого сценария производился расчет ЧДД, а полученные значения использовались для построения гистограмм и графиков кумулятивной вероятности. Такие графики для базового и коммерческого вариантов показаны на рис. 13.6, из которого следует, что оценки вероятности ЧДД = 0 составили для коммерческого варианта 98 %, а для базового варианта - лишь около 10 %. [c.242]
Первичные данные о доходах были трансформированы в ряд распределения, который имеет интервалы шириной 1%, начиная с —8% и заканчивая + 12%. Эти данные будут использованы для составления графиков распределения частот, распределения относительных частот, распределения кумулятивных частот и гистограмм. Данные для построения рядов распределения частот приведены в табл. 2.4. [c.72]
Следующим шагом в представлении относительного распределения будет его отображение не высотой, а площадью столбиков. Данное графическое представление известно как гистограмма. Для иллюстрации построения гистограммы рассмотрим следующие сгруппированные данные [c.74]
Графическое изображение ряда распределения может быть получено также с помощью полигона. По вертикальной оси этого графика откладывают те же величины, что и при построении гистограммы. По горизонтальной оси откладывают средние точки групп. Таким образом, линейный график, по одной оси которого отложены частоты групп, а по другой — их средние точки, называют полигоном. [c.219]
Гистограмма распределения реализаций случайной величины применяется для графического изображения интервальных рядов распределения. Она представляет собой многоугольник, построенный с помощью смежных прямоугольников. В случае непрерывных равных интервалов с шириной интервала Ах гистограмма строится следующим образом (рис. 1.3). [c.19]
Гистограммы чаще всего применяются для изображения вариационных рядов с непрерывными значениями случайной величины X. При уменьшении величины каждого интервала гистограмма будет приближаться к некоторой плавной кривой, соответствующей графику функции плотности распределения случайной величины X. Следовательно, в результате построения гистограммы можно получить представление о дифференциальном законе распределения случайной величины X. [c.20]
При непрерывной вариации используют, как известно, интервальные вариационные ряды, графическим изображением которых служит гистограмма. Для построения гистограммы по оси абсцисс в соответствии с принятым масштабом откладывают границы интервалов. Эти интервалы являются основаниями прямоугольников, площади которых равны либо пропорциональны частотам или частостям распределения в соответствующих интервалах. [c.57]
| Рис. П.1а. Гистограмма распределения населения России по совокупным душевым расходам, построенная на базе исходных (некалиброванных) данных | 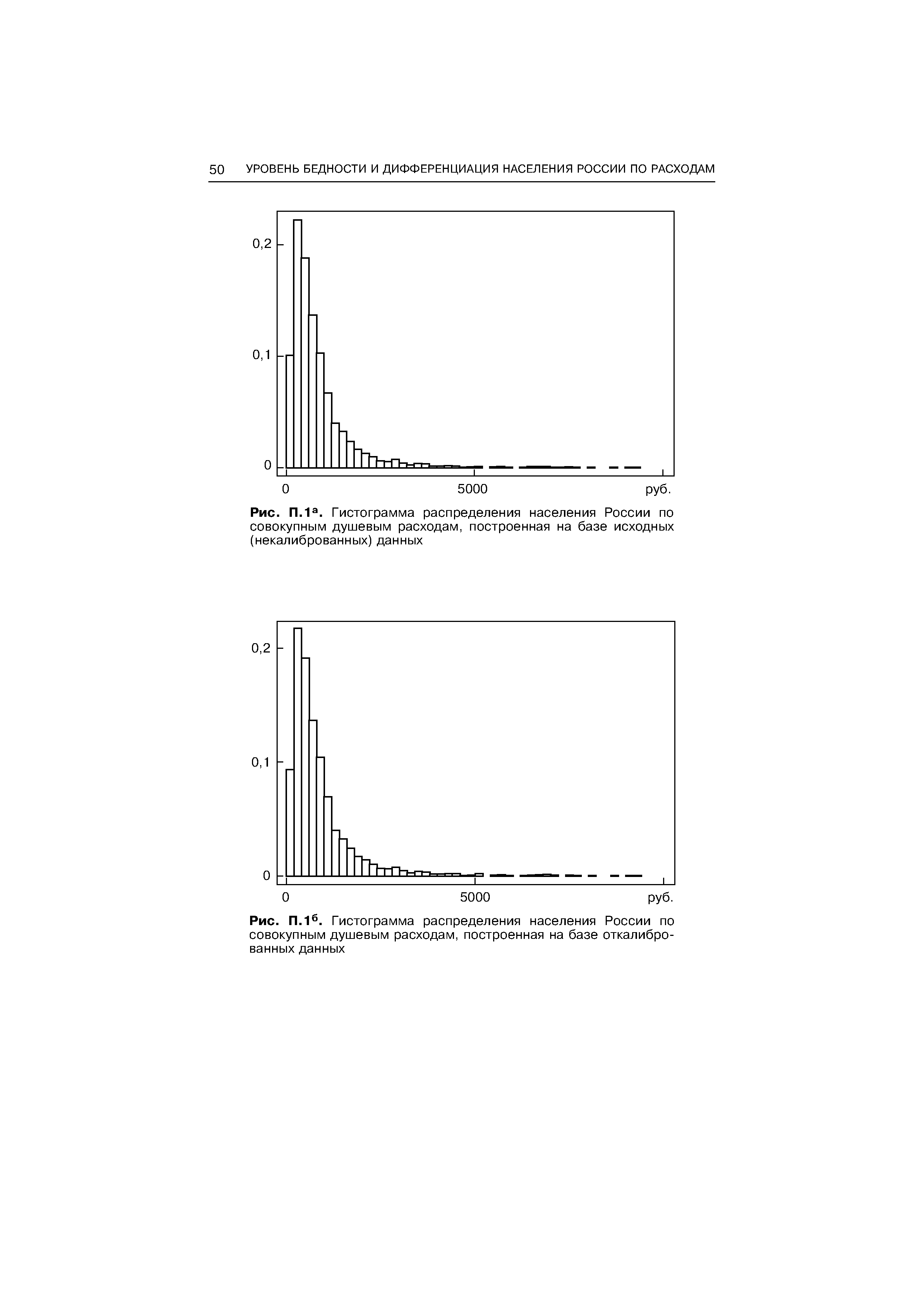 |
Проверка статистических гипотез о виде распределения случайных величин. При построении математической модели исследуемых процессов часто возникают задачи сопоставления полученного материала экспериментов с известными теоретическими распределениями. Если сопоставить вероятность попадания в интервалы, на которые разбита выборка, с соответствующими частотами, полученными из наблюдений, или проводить графическое сравнение полигонов и гистограмм с некоторой теоретической функцией распределения, то можно получить представление о степени близости теоретического и эмпирического распределений. [c.72]
Правдоподобна или нет гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, можно определить уже по виду гистограммы, построенной на основании экспериментальных данных. Порядок ее построения рассмотрен в примере 13. Наглядность отображения гистограммой закона распределения вероятности результата измерения зависит от соблюдения следующих правил при ее построении [c.104]
Поскольку, как уже говорилось выше, из полигона распределения легко можно получить гистограмму и наоборот, использование данного метода рассмотрим в предположении, что исходным графиком является гистограмма. В случае, если известен только полигон распределения, мы можем восстановить по нему гистограмму, тщательно его измерив и определив опорные точки (середины интервалов) этого полигона, и затем применить изложенный метод непосредственно к гистограмме. Относительно способа ее построения примем следующие допущения. [c.232]
Гистограмма — кривая, построенная по крайним верхним точкам разброса статистических данных относительно среднего значения (медианы). Гистограмма характеризует нормальность распределения. Распределения могут быть нормальными (рис. 17.6, а), [c.472]
Гистограмма — кривая, построенная по крайним верхним точкам разброса статистических данных относительно среднего значения (медианы). Гистограмма характеризует нормальность распределения. Распределения могут быть нормальными (рис. 4.6, а), островершинными (рис. 4.6, 6), плосковершинными (рис. 4.6, в), смещенными влево или вправо относительно центра (рис. 4.6, г). Для оценки гистограммы применяются следующие критерии среднеквадратическое отклонение, коэффициенты вариации, корреляции, асимметрии, эксцесса, критерии Фишера, Стьюдента и др. (подробнее см. учебник автора по управленческим решениям.1 На рис. 4.6, а и б технологические процессы протекают нормально, система станок — приспособление — инструмент — деталь отлаженная, на рис. 4.6, виг эта система требует отладки. [c.202]
Ее ли исходить из гипотезы, что величины А 1, АЗ,. . . одинаково распределены и независимы (это предположение дает возможность обоснования, опираясь на закон больших чисел, состоятельности обычных статистических процедур построения оценок параметров, распределений и т. д.), то наглядное представление о характере их распределения вероятностей можно получить из гистограммы (эмпирической плотности) р (А), построенной по имеющимся статистическим данным. [c.389]
Как известно, плотность распределения — это число единиц совокупности, приходящееся на единицу ширины интервала. При равных интервалах плотность распределения прямо пропорциональна частотам или частостям, которые и используются для построения прямоугольников. При неравных интервалах гистограмма строится только по плотности распределения. [c.57]
Для обучения СОК, описываемой в этой главе, мы использовали финансовые показатели, построенные на основании данных финансовой отчетности. Перед началом обучения финансовые показатели подверглись предварительной обработке. В качестве метода было выбрано выравнивание по гистограмме, поскольку, на наш взгляд, оно несколько больше подходит для последующей обработки при помощи СОК, чем выравнивание по дисперсии. Метод выравнивания по гистограмме позволяет преобразовать произвольное исходное распределение значений показателей в почти равномерное. [c.106]
Программа LAWX предназначена для определения закона распределения случайных непрерывных величин при помощи критерия согласия J,, о котором говорилось в разделе 2.3, а также расчета статистических параметров выборки и построения гистограммы эмпирического распределения. [c.146]
Как указывалось (раздел 7.9), гистограмма распределения частот может быть описана распределением Пуассона. Можно использовать Пуассонову диаграммную бумагу для построения карт, показывающих уровень вероятности, соответствующий пределам корректировки и предупреждения для любой вероятности, а не только для уровней За и 2сг, которые обычно используются. Можно также использовать таблицы для построения пределов корректировки и предупреждения при любых заданных вероятностях. [c.132]
Построение гистограмм по каждому фактору с целью определения форм распределения случайных наблюдений. Построение по каждому фактору корреляционных полей, т. е. графическое изображение функций от фактора с целью предваритель- [c.322]
Построенные на основании данных таблицы П3.1 гистограммы распределения факторов скоринга представлены на рис П3.1- П3.8. [c.57]
Предшествующий опыт кластеризации на основе гистограмм распределения факторов [69], построенных при сводном анализе широкого перечня эмитентов ценных бумаг, приводит нас к результатам, котороые сведены в таблицу П4.3. Поскольку все факторы по построению являются относительными характеристиками, то они выражены в процентах. [c.67]
Диаграмма Парето объединяет в себе гистограмму и кумуляту, размещенные на прямоугольной основе системы координат. Гистограмма представляет собой набор столбиков, которые иллюстрируют измеряемую величину, например количество сведенных в конкретные группы дефектов. Кумулята — это возрастающая ломаная линия, отражающая процесс последовательного наращивания столбиков гистограммы. Порядок построения диаграммы очень прост , а) сбор информации о причинах брака, сведение причин в отдельные группы б) распределение полученных данных по осям координат. Обычно издержки производства от дефектов откладываются на вертикальной шкале, а причины дефектов — на горизонтальной в) вычерчивание столбиков гистограммы г) вычерчивание кумуляты. [c.138]
Программное обеспечение системы. Для управления проектом используется программная система управления проектами Time Line , позволяющая осуществлять автоматизированное планирование сроков выполнения работ, распределение ресурсов, построение ресурс-гистограмм, график Ганта и сетевых [c.458]
Вариационный ряд помогает определить долю неответивших респондентов табл. 15.2 один респондент из 30 не ответил на вопрос), а также указывает долю ошибочных ответов. Значения, равные 0 или 8, соответствуют ошибочным ответам. Следует определить количество случаев с такими значениями и соответственно откорректировать результат. Кроме того, можно установить наличие выбросов, т.е. случаев с экстремальными значениями. При анализе распределения частот относительно размера домохозяйства (семьи) выбросами следует считать несколько семей, состоящих не меньше чем девяти человек. Распределение частот также определяет форму эмпирического распределения значений переменной. Частотные данные можно использовать для построения или вертикальных столбчатых диаграмм, на которых по оси значения переменной, а по оси 7— абсолютные (частоты) или относительные (частости) значения. На рис. представлена гистограмма для данных табл. 15.2. По гистограмме можно проверить, соответствует ли наблюдаемое распределение предполагаемому маркетологом распределению. [c.557]
Смотреть страницы где упоминается термин Построение гистограммы распределения
: [c.11] [c.145] [c.110] [c.22]Смотреть главы в:
Статистика для трейдеров -> Построение гистограммы распределения
