Можно построить в системе координат (х, т) график с точками (Xj, w,), (x2, /и2),..., (xk, т,) и соединить полученные точки ломаной линией, которую называют полигоном частот выборки или полигоном распределения (рис 2.1). [c.38]
Аналогично все указанные приемы обработки и построения могут быть распространены и на другие показатели, например на объемы поставок, интервалы между поставками, объемы суточных отпусков и суточных объемов поставок. Эти полигоны распределения описывают, как в течение отчетного года на предприятии изменялись объемы поставок, интервалы поставок и объемы суточных отпусков и т.д. [c.78]
Любой полигон описывается набором средних значений интервалов (диапазонов) вариаций какого-либо одного признака и частостью появления этого среднего значения. Каждый из полигонов распределения можно выразить аналитически, например, для ряда распределения объемов поставок (Q, W), формула будет выглядеть следующим образом [c.78]
Аналогично аналитически можно выразить полигоны распределения интервалов между поставками (Т, У) и объемов суточных отпусков (R, СО [c.78]
Полигон распределения — ломаная линия, построенная на графике и характеризующая изменение вероятностей различных исходов событий при повторных испытаниях. [c.209]
Следующей задачей является оценка возможных сочетаний значений нормообразующих факторов, которые могут иметь место в интервалах отгрузки в плановом году. Возможность получения результата вытекает из анализа данных, приведенных на рис. 5.8 и 5.9. На каждом из этих 12 графиков построены два полигона распределений вариаций значений нормообразующих факторов в целом за три года и за один год из этого же периода. Они построены по четырем предприятиям — горно-обогатительному и лесообрабатывающему комбинатам и двум машиностроительным заводам. На графиках по осям абсцисс отложены диапазоны вариаций значений нормообразующих факторов на каждом из этих предприятий, а по осям ординат — частости появления значений признаков в соответствующих периодах. Штриховые линии полигонов, проведенные на графиках, построены по результатам обработки фактических данных за один отчетный год (1), сплошные — в целом за трехлетний период (Z). [c.223]
Поскольку, как уже говорилось выше, из полигона распределения легко можно получить гистограмму и наоборот, использование данного метода рассмотрим в предположении, что исходным графиком является гистограмма. В случае, если известен только полигон распределения, мы можем восстановить по нему гистограмму, тщательно его измерив и определив опорные точки (середины интервалов) этого полигона, и затем применить изложенный метод непосредственно к гистограмме. Относительно способа ее построения примем следующие допущения. [c.232]
В табл. 6.3.1 показаны все необходимые исходные данные, позволяющие рассчитать эмпирическую функцию распределения, гистограмму и полигон распределения. [c.313]
Ниже на рис. 6.3.10 и 6.3.11 приведены гистограмма и полигон распределения относительных частот. [c.314]
II. Диаграммы 1. Диаграммы рас- а) ДГ распределения по одному полигон распределения гистограмма [c.55]
Вариационные ряды могут быть изображены графически в виде полигона распределения и гистограммы. [c.18]
М . .. MJ. .. Mk. Крайние точки MI и Mk, если они не лежат на оси Оде, соединяют также со смежными точками соответственно MQ(XQ, 0) и Mk+i(xk+i, 0) на оси абсцисс. Полученный таким образом многоугольник MQ Л/i М2. .. Mt. .. Mk Mk+i является полигоном распределения. [c.19]
| Рис. 1.2. Полигон распределения реализаций случайной величины X | 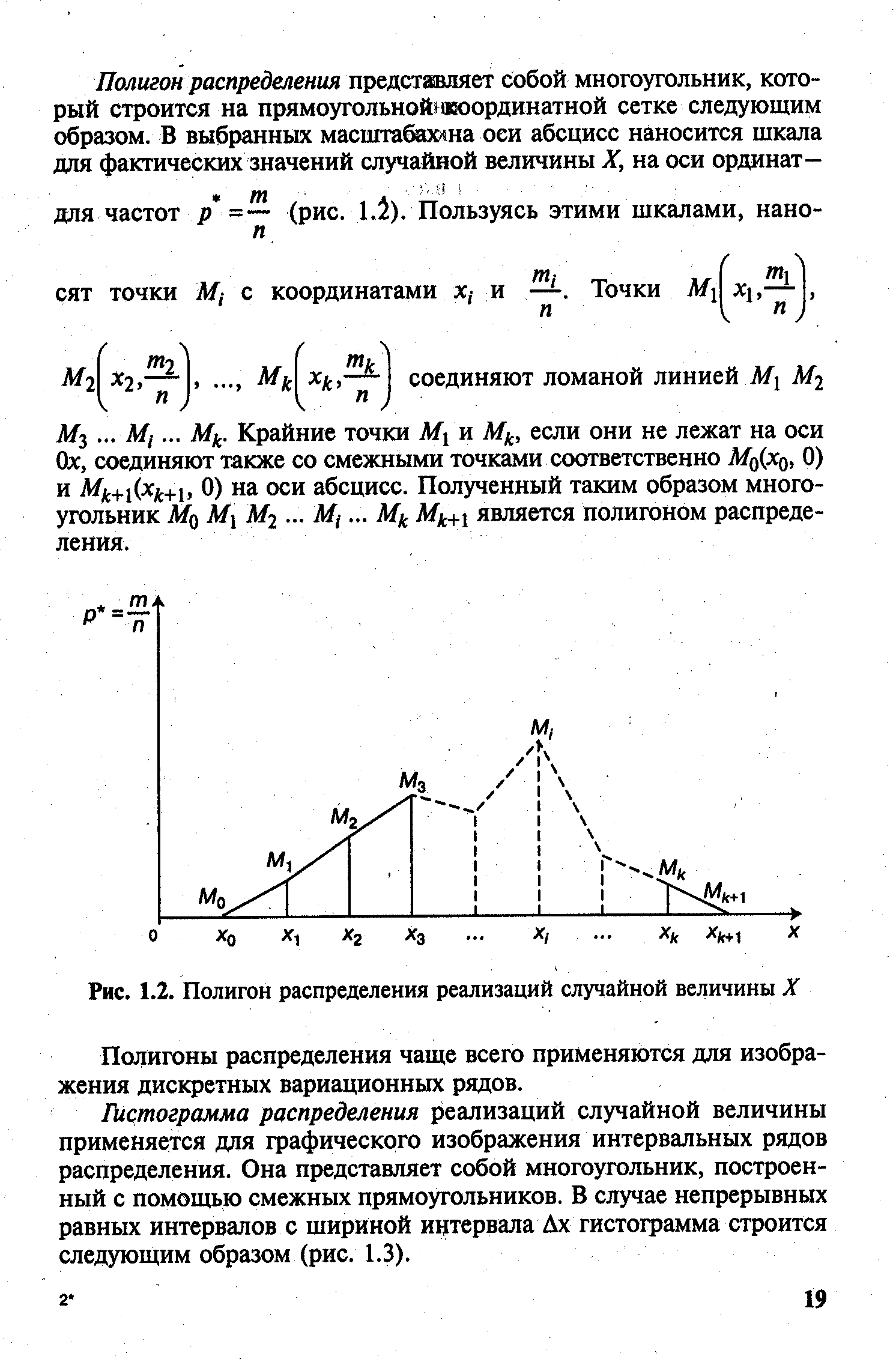 |
Полигон распределения и гистограмма есть реализация распределения выборочной совокупности при ограниченном числе наблюдений (N), а предельная кривая при N — > °° является распределением генеральной совокупности. Распределение генеральной совокупности является теоретическим распределением. Отдельные распределения изучены и поддаются точному аналитическому опи- [c.24]
Если уменьшить интервалы и одновременно увеличивать число наблюдений при конечной численности группы, то полигон распределения и гистограмма станут приближаться [c.81]
Для изображения вариационных рядов применяются линейные и плоскостные диаграммы, построенные в прямоугольной системе координат. При дискретной вариации признака графиком вариационного ряда служит полигон распределения. Рассмотрим пример его построения по следующим данным. [c.56]
Полигон распределения представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующегося признака, а ординатами — соответствующие им частоты (рис. 3.8). [c.56]
Наглядно ряды распределения можно представить при помощи их графического изображения, позволяющего судить о форме распределения. Наиболее часто для этой цели используют полигон и гистограмму. [c.31]
На графике (рис. 4.1) представлены полигон (ломаная прямая) и гистограмма (совокупность прямоугольников) вышеуказанного распределения. [c.33]
Проверка статистических гипотез о виде распределения случайных величин. При построении математической модели исследуемых процессов часто возникают задачи сопоставления полученного материала экспериментов с известными теоретическими распределениями. Если сопоставить вероятность попадания в интервалы, на которые разбита выборка, с соответствующими частотами, полученными из наблюдений, или проводить графическое сравнение полигонов и гистограмм с некоторой теоретической функцией распределения, то можно получить представление о степени близости теоретического и эмпирического распределений. [c.72]
Полигон степени влияния отобранных факторов на изучаемый показатель - распределение суммы рангов влияния факторов на изучаемый показатель. Если соединить его начало и конец прямой линией, то можно видеть, насколько далека полученная ранжировка от ранжировки, соответствующей полной согласованности мнений опрашиваемых экспертов. При этом возможны три случая ранжировки [c.123]
Преимущества пробного маркетинга заключаются в том, что информация, которую можно получить с его помощью, облегчает принятие решения о выведении нового товара в общенациональных масштабах (или о необоснованности такого выведения), а также в том, что появляется возможность проверить эффективность таких элементов маркетингового комплекса, как цена, формула/упаковка товара, продвижение и распределение. Иногда используется несколько испытательных полигонов с разными комбинациями маркетингового комплекса, что позволяет спрогнозировать наиболее успешную стратегию выведения товара на рынок. Цель такого подхода — снизить риск тяжелой и дорогостоящей ошибки, связанной с выведением товара на общенациональный рынок. [c.270]
Изучая социальную организацию, социологии также выделяют различные уровни, например микроуровень (индивидуальный и групповой) и макроуровень, или общество. Используемые понятия и рассматриваемые явления изменяются в зависимости от уровня. При этом также существуют взаимозависимости и взаимодействия между различными уровнями. Изменения на макроуровне могут повлиять на ожидания и поведение людей на микроуровне и наоборот. Например, появление автомобилей радикально изменило мобильность человека (потребителя), что оказало влияние на покупательское поведение, а также на структуру системы распределения. Это, в свою очередь, отразилось в радикальных переменах в области розничной торговли. Снижение уровня рождаемости, например, вызванное пессимистическим отношением к будущему, может привести к значительным изменениям спроса на определенные товары и услуги. Такие демографические изменения, кроме всего прочего, изучаются социологами, а на практике их ощущают маркетологи. Различные рынки также использовались в качестве полигонов для проведения социологических исследований, которые способствовали совершению важных открытий и при этом оказывались полезными для маркетинга. [c.155]
Построим кривую распределения (полигон) (рис. 6.6). Определим размах [c.220]
Полигон — это графическое изображение дискретного вариационного ряда [X, W] в прямоугольной системе координат, при котором величины признака X откладываются на оси абсцисс, а соответствующие им частости W — на оси ординат. Эти точки соединяются отрезками прямой, полученная фигура представляет распределение совокупности по признаку X. [c.78]
Для расчета специфицированных норм производственных запасов требуется перейти от аналитической записи каждого полигона к вероятностным характеристикам — плотностям распределения вариаций объемов поставок (или соответственно интервалов поставок, объемов суточных отпусков и т.п.). Построенная же по полигону плотность распределения вариаций этого признака — Р(Х X показывает, как будут изменяться вариации признака X в плановом году. Далее будет более подробно пояснено, что эти плотности распределения обладают свойством устойчивости, по ним можно рассчитать специфицированные нормы производственных запасов для планового года. Причем будет показано, что чем больше неравномерность (размах вариаций фактора), тем выше должно быть установлено значение определяемой нормы производственного запаса при прочих одинаковых или примерно одинаковых условиях (например, при одном и том же годовом объеме поступления, одинаковых частотах поставок и годовом объеме расхода и т.д.). [c.79]
Разберем, как от аналитического выражения полигона вариаций признака (например, для объемов поставок — Q, W) перейти к плотности распределения вариаций этого же признака — Q, P(Q). Здесь для двух указанных выше случаев применяются разные обозначения величины вариаций объемов поставок и разные обозначения изменений частости объемов поставок и их вероятностей. В первом случае данные но отчетному [c.79]
Графически вариационные ряды изображаются в форме кривой распределения или полигона частоты. Приведем пример. [c.262]
Из цифрового и графического изображения рядов видно, что во втором году произошло значительное улучшение распределения долблений по уровням механических скоростей. Так, во втором году первый интервал оказался совершенно не заполненным, ряд стал короче и вершина полигона сдвинулась вправо к большим показателям скоростей. [c.262]
| Рис. 13. Гистограмма, полигон и плотность распределения вероятности отсчета у аналогового измерительного прибора | 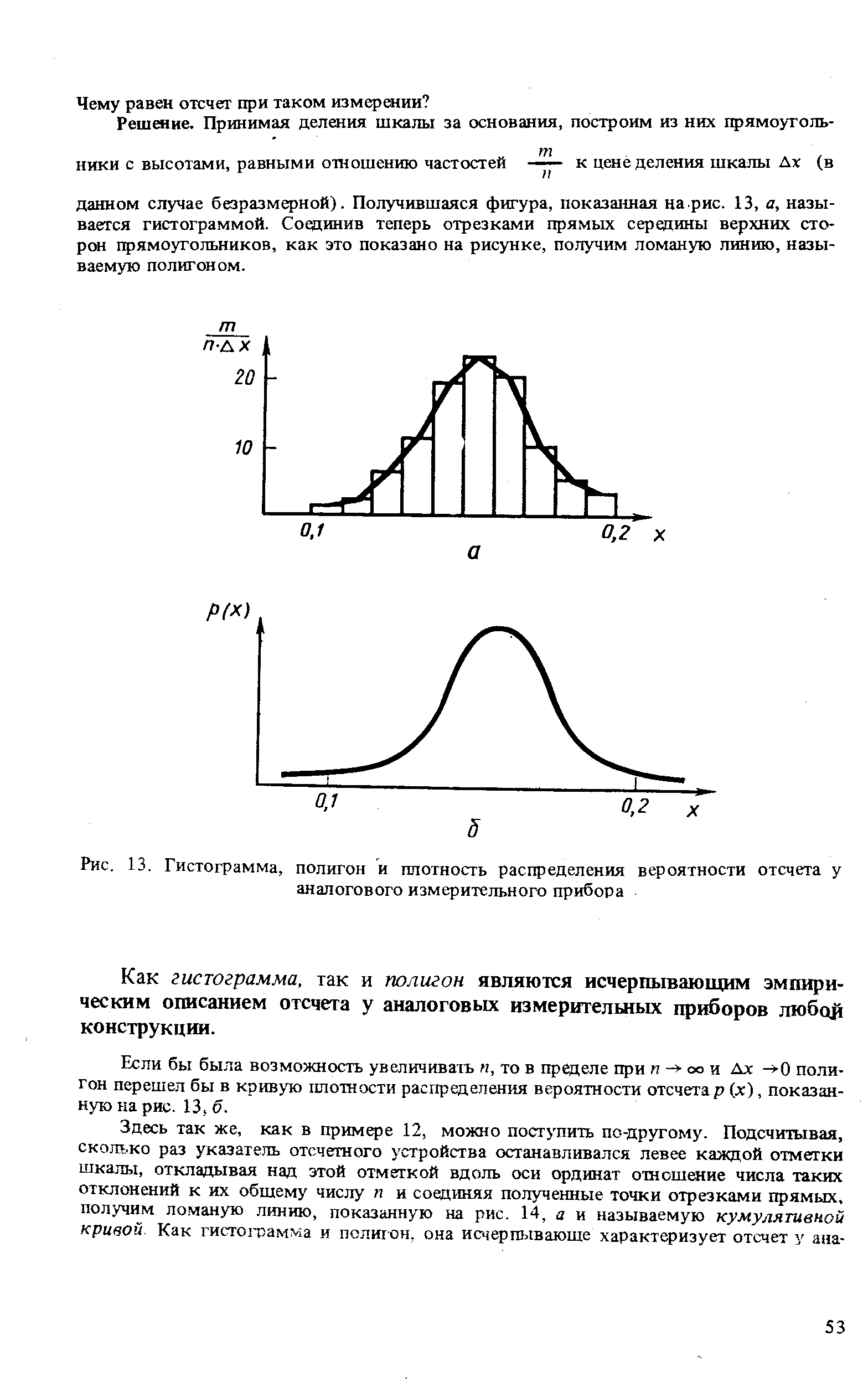 |
Вариация данных анализируется с помощью полигона распределения, кумуляты (кривой меньше, чем ) и огивы (кривой больше, чем ). Все эти виды графиков рассматриваются в главе 5. Линейные графики используются в решении задач классификации данных (см. гл. 6). Применение линейных графиков в анализе динамики рассмотрено в главе 9, а использование их для анализа связей -в главе 8. В этих же главах рассмотрено использование точечных диаграмм (см., например, поле корреляции в гл. 8). [c.64]
Полигон распределения представляет собой многоугольник, который строится на прямоугольной) оооординатной сетке следующим образом. В выбранных масштабахша оси абсцисс наносится шкала для фактических значений случайной величины X, на оси ординат- [c.19]
Построим полигон, гистограмму, кумуляту и огиву (рис. 4.1) на основании следующих данных о распределении сельского населения в России на 1 января 1998 г. по возрастным группам (млн человек). [c.32]
| Рис. 4.1. Полигон и гистрограмма распределения сельского населения России по возрасту | 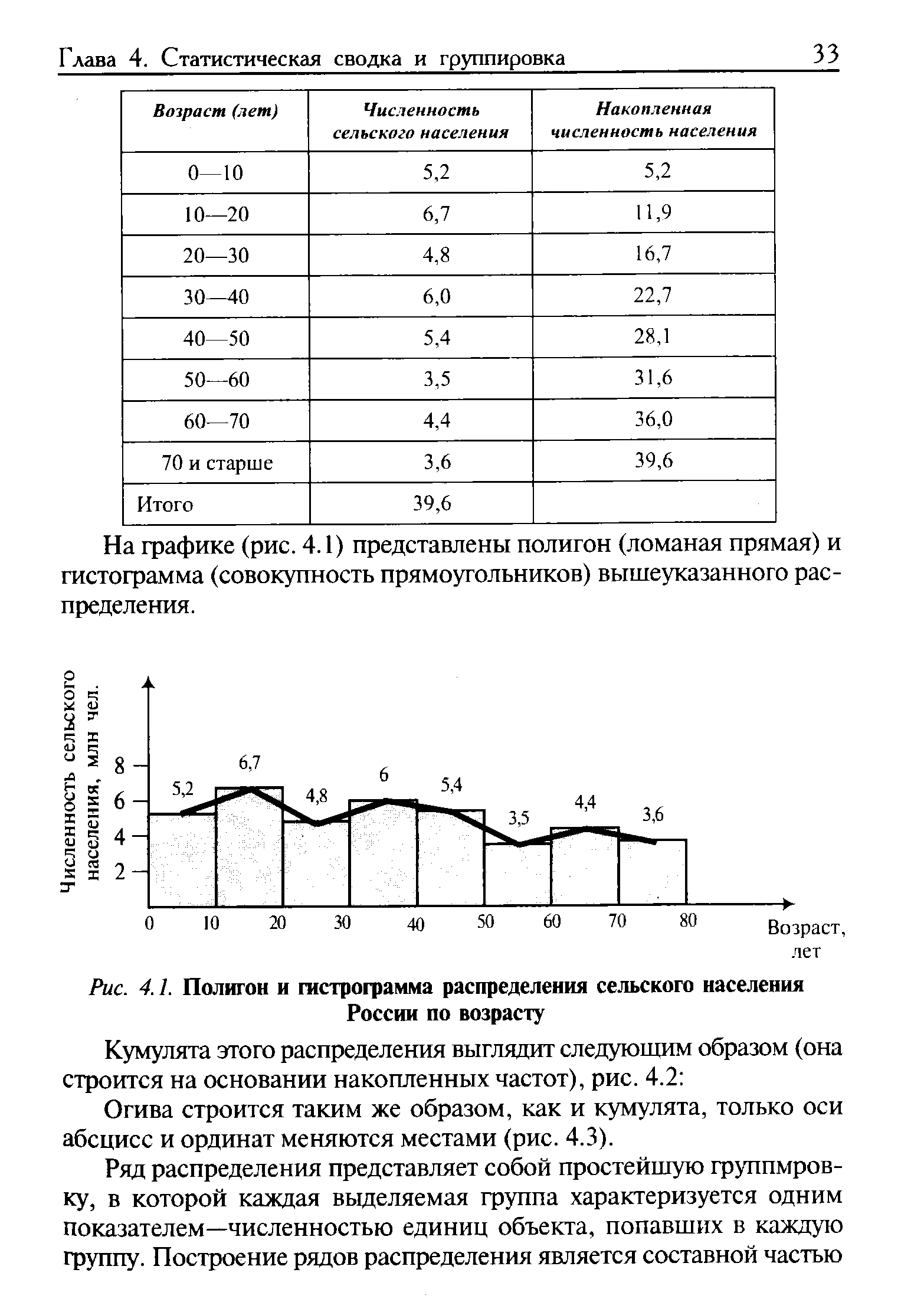 |
Для наглядности определения закономерностей изменения признака ряд распределения целесообразно представлять вчвиде полигонов (так как все изучаемые в настоящей работе признаки характеризуются дискретными величинами). Для изображения ряда распределения графически необходимо определение размера интервала группировок исходных данных. [c.189]
Для графического изображения рядов распределения кроме гистограммы и полигона могут применяться также кумулятивная кривая и огива1. [c.122]
Накоплен опыт применения технологий ГИС для хранения, манипулирования, обработки и отображения (визуализации) пространственных и, в частности, географических данных в различных форматах растрового и векторного представления информации [Воробьев и др., 1995 Васильев и др., 1996 в By hkov e.a., 1998]. Ведется разработка нескольких пилотных ГИС, например, экологического WWW-атласа региона, ГИС Загрязнение Братского водохранилища и Байкальский геоэкологический полигон . Возрастающее значение приобретают удаленный съем информации как ценный источник природных данных (аэро- и космические снимки и и улучшения визуализации. Пока недостаточно развиты возможности взаимодействия пространственно-распределенных моделей с ГИС. Далее будет более подробно описано использование ГИС-технологий в Администрации Иркутской области. [c.243]
Физический смысл полигонов вариаций значений нормообразующих факторов, приведенных на рис. 5.8 и 5.9, состоит в следующем они показывают, как изменялись условия производства и отгрузки готовой продукции на предприятиях в отчетных периодах. Из графика, приведенного на рис. 5.8г, следует, что объемы суточного производства пиломатериалов на лесодеревообрабатывающем комбинате ЛДК-4 изменялись в диапазоне от 100 до 900 куб. м (т.е. размах вариаций их будет от Rmia = 100 до -Rmax = 900 куб. м/сутки). Объемы производства пиломатериалов 430 куб. м/сутки составляли основную долю 44% (Р(Ю - 0,44), 580 куб. м/сутки — 28%, 690 куб. м/сутки — 4% и т.д. На рис. 5.8д и 5.8е построены распределения вариаций суточных объемов отгрузок пиломатериалов и интервалов между отгрузками, которые были в отчетном периоде. Объемы суточных отгрузок менялись в диапазоне от 50 до 780 куб. м/сутки (рис. 5.8д). В основном они составляли по 200-500 куб. м/ сутки - 45% (Р(О) = 0,45 при О = 200-580 куб. м/сутки), 580 куб. м/ сутки — 13%, 640 куб. м/сутки — 4% и т.д. [c.223]
