В экономическом анализе применяются почти все виды графиков диаграммы сравнения, диаграммы временных рядов, кривые распределения, графики корреляционного поля, статистические картограммы. Особенно широко распространены в анализе диаграммы сравнения — для сравнения отчетных показателей с плановыми, предшествующих периодов и передовых предприятий отечественных или зарубежных. Для наглядного изображения динамики экономических явлений (а в анализе с динамическими рядами приходится иметь дело очень часто) используются диаграммы временных рядов. [c.152]
Тип кривой выбирается на основе сочетания теоретического анализа и исследования исходных эмпирических данных. Теоретический анализ наряду с обычными логическими сопоставлениями известных научных понятий включает опыт предыдущих исследований, экспертные оценки специалистов. Эмпирический путь заключается в изучении имеющихся исходных данных посредством построения корреляционных полей и эмпирических линий регрессии, а также анализа параллельных рядов, в результате которого исследуются разности между парами значений признаков (увеличивающиеся и уменьшающиеся абсолютные разности, постоянные и изменяющиеся относительные роста и т.д.). Изучение эмпирического материала показывает наличие или отсутствие связи, ориентирует ее направление и форму. Так, если результативный признак по сравнению с факторным увеличивается с одинаковой скоростью — связь прямолинейная, одинаковым темпом — связь экспоненциальная и т.п. [c.320]
Коэффициент корреляции может принимать как положительные, так и отрицательные значения. Знак при г совпадает со знаком коэффициента регрессии. Нетрудно сообразить, что г находится в границах -1 s г +1. При г = +1 или г = -1 все точки корреляционного поля лежат на прямой. В этом случае имеет место строгая пропорциональность в изменениях у и х. [c.323]
Этап 2, Данные из таблицы наносятся на плоскость координат — строится корреляционное поле. [c.50]
| Рис. 11.1. График корреляционного поля | 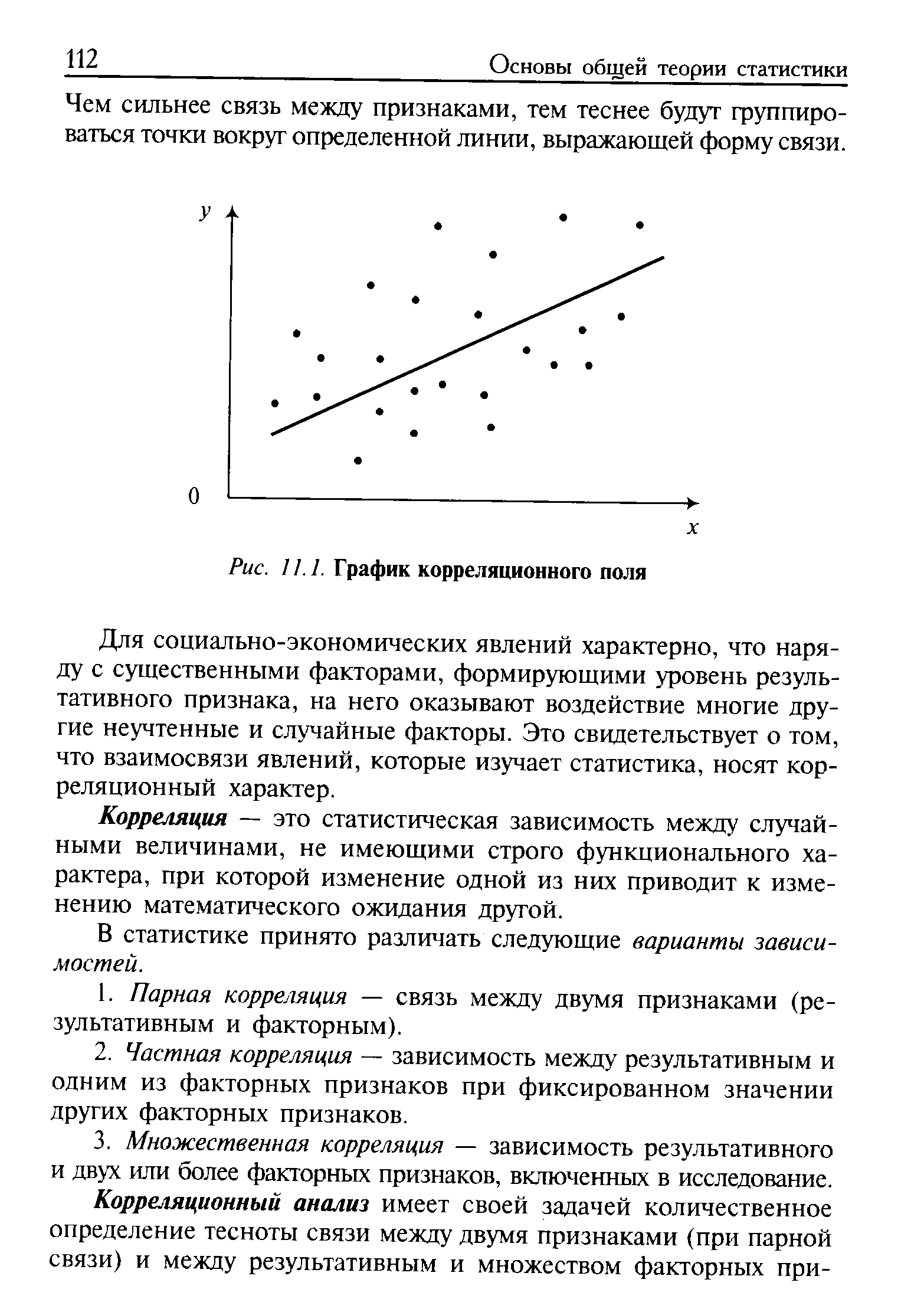 |
Две корреляционные зависимости переменной Y от X приведены на рис. 3.2. Очевидно, что в случае а зависимость между переменными менее тесная и коэффициент корреляции должен быть меньше, чем в случае б, так как точки корреляционного поля а дальше отстоят от линии регрессии, чем точки поля б. [c.57]
Следует отметить, что мы ввели выборочный коэффициент корреляции г исходя из оценки близости точек корреляционного поля к прямой регрессии Y по X. Однако г является непосредственно оценкой генерального коэффициента корреляции р между X и У лишь в случае двумерного нормального закона распределения случайных величин X и У В других случаях (когда распределения Хи У отклоняются от нормального, одна из исследуемых величин, например X, не является случайной и т.п.) выборочный коэффициент корреляции не следует рассматривать как строгую меру взаимосвязи переменных. [c.59]
| Рис. 1.5. Зависимость. между весом машин и себестоимостью их изготовления (пример построения корреляционного поля) |  |
Проводимый анализ даже небольшого объема статистического материала дает возможность установить корреляционные зависимости между себестоимостью производства однотипных машин аналогичного эксплуатационного назначения и их наиболее характерными параметрами. Такие корреляционные зависимости характеризуются тем, что одному и тому же значению аргумента (в данном случае параметру машины) соответствует несколько значений функции (себестоимости). При построении корреляционного поля отчетливо прослеживается, что изменение параметра-аргумента вызывает закономерное изменение функции (рис. 4.3). [c.121]
Постройте корреляционное поле и сформулируйте гипотезу о форме связи. [c.8]
Совокупность точек, представленных табл. 11, образует так называемое корреляционное поле, изображенное на рис. 41а. [c.171]
Очевидно, что если все точки корреляционного поля лежат на линии f(x 1), то aij.i = 0. Отсюда можно построить коэффициент связи [c.80]
Обращаясь к диаграмме рассеяния (рис. 6.1), отметим, что через точки на графике можно провести несколько прямых линий, удовлетворяющих выражению (6.1), хотя в действительности невозможно построить одну прямую линию, которая пройдет через все точки корреляционного поля. Отсюда очевидно, что нужно выбрать лишь одну линию. [c.264]
| Рис. 1.1. Корреляционное поле, характеризующее связь между численностью населения и числом установленных телевизионных точек т) в США в 1953 г. а) в девяти городах б) в десяти городах |  |
Анализ парных корреляционных полей состоит обычно в следующем [c.181]
В результате такого анализа обычно получают формулировку нескольких рабочих гипотез об общем виде искомой зависимости, окончательная проверка которых и выбор наиболее адекватной из них осуществляются (при отсутствии априорных сведений содержательного характера) с помощью соответствующих математико-статистических методов. Описание наиболее эффективных, с нашей точки зрения, приемов такого типа приводится в 6.3. Здесь же остановимся на двух вспомогательных приемах, которые полезно использовать при геометрическом анализе парных корреляционных полей. 6.2.2. Учет и формализация гладких свойств искомой функции регрессии. Выше упоминалось, что чрезмерное усложнение класса допустимых решений F и, в частности, завышение порядка аппроксимирующего регрессионного полинома (в но- [c.181]
Корреляционное поле 181 Корреляционный анализ 49, 56 Коэффициент конкордации (согласованности) 116—117 [c.473]
Применение корреляционного анализа позволяет установить наличие или отсутствие связи между изучаемыми величинами в условиях действия большого числа факторов, ряд из которых неизвестен. Наличие или отсутствие связи определяется путем составления уравнений связи или, как их принято называть, уравнений регрессий. Форму связи (прямолинейную или криволинейную) определяют на основе предварительного анализа. О наличии корреляционной связи, а также о форме и характере кривой в первом приближении может дать представление графический анализ распределения совокупности точек, образующих корреляционное поле. Так, вытянутый характер расположения точек и ось контура корреляционного поля, составляющая острый или тупой угол с осями координат, свидетельствуют о наличии корреляционной связи и прямолинейной формы связи. Если наибольшая ось контура корреляционного поля параллельна одной из осей координат или контур поля приближается к форме круга, то такое соотношение исследуемых факторов не имеет или почти не имеет корреляционной связи. [c.114]
Распределение точек в системе координат при влиянии большего количества факторов характеризуется большим или меньшим их разбросом даже при определенно выраженной форме связи. В связи с этим внутри корреляционного поля всегда можно провести значительное количество линий, выражающих данную форму. Задача исследователя состоит в проведении линии наиболее вероятной, наиболее точно выражающей зависимость исследуемой величины от изменения того или иного фактора. Практически это решается применением метода наименьших квадратов, т. е. сводится к минимизации указанного в формуле (с. 111) выражения, где сумма охватывает все точки выборки. [c.114]
Если провести прямые линии параллельно оси абсцисс и оси ординат через точки (х, у) средних значений х и у, то плоская поверхность, по которой разбросаны точки, окажется разделен-. ной на четыре части. Как показано на рис. 9.1, это называют I, II, III, IV секторами корреляционного поля. [c.155]
IV. Диаграммы 1. Диаграммы кон- корреляционное поле точечные и фоновые ДГ [c.55]
На первом этапе рекомендуется попытаться установить зависимости между внешними (внутренними) факторами и уровнем риска. Количество зависимостей определяется полнотой и качеством информационного обеспечения системы управления рисками. Для этих целей следует строить корреляционные поля (рис. 5.3) и устанавливать статистические зависимости. [c.200]
| Рис. 5.3. Корреляционные поля зависимостей уровня риска (Y) от факторов |  |
Для установления силы влияния (корреляции) одного фактора на другой и направленности взаимодействия строят корреляционные поля (диаграммы рассеяния) — рис. 17.8. Анализ рисунка показывает, что связь между Х и Y тесная, прямолинейная, [c.473]
| Рис. 17.8. Корреляционные поля (диаграммы рассеяния) | 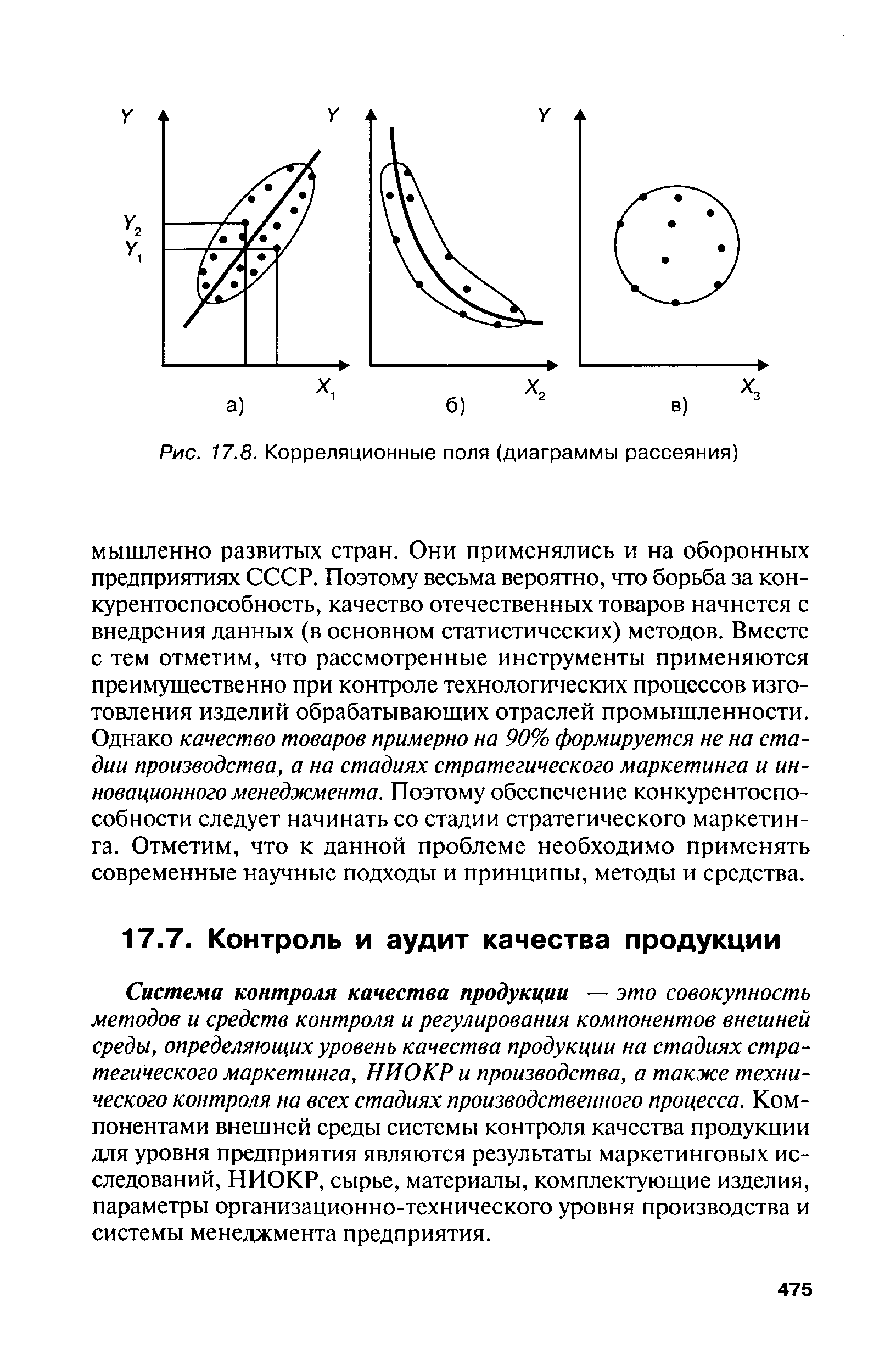 |
Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной свв-зи, когда все точки лежат на линии регрессии ух =5 ДчО ТО фактические значения результативного признака совпадают с теоретическими у = ух, т. е. они полностью обусловлены влиянием факторах. В этом случаеостаточная дисперсия Вост — 0. Впрйктичёб-ких исследованиях, как правило, имеет место некоторое рЙссея-ние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических (у — ух). Величина этих отклонений и лежит в основе расчета остаточной дисперсии [c.40]
Аппарат, используемый А. Ноткиным, — числовые модели роста национального дохода и фонда потребления в зависимости от нормы Производственного накопления. Здесь сразу же следует поставить вопрос возможно ли статистическое изучение Конечно, данные о динамике нормы производственного накопления за ряд лет (аналогичные приведенным выше) позволяют сделать определенные выводы о политике капитальных вложений за весь период экономического развития нашей страны и с этой точки зрения весьма полезны. Однако они не могут ответить на вопрос, насколько величина нормы накопления данного года приближается к оптимальной. Не поможет и коррелирование фонда потребления от нормы производственного накопления, которое, вообще говоря, возможно (поскольку для каждого года экономического развития можно выявить точку корреляционного поля), но методологически неверно, ибо условия различных лет несопоставимы (разная производительность общественного труда, разная фондоемкость продукции, различно число занятых в процессе материального производства и т. д.). Естественно, что для каждого отдельного года существует лишь одна норма производственного накопления. Итак, на вопрос о возможности статистического изучения оптимума накопления и потребления для данного периода следует ответить отрицательно. Остаются два пути числовое моделирование и математическое моделирование. [c.37]
Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость. Часто при рассмотрении парных корреляционных полей ни линейная, ни полиномиальная регрессия не дают желаемой точности приближения. В этих случаях приходится обращаться к другим видам зависимостей гиперболической, степенной, показательной и др. Покажем, что в ряде ситуаций эти зависимости оказываются не менее удобными, чем линейная, поскольку легко к ней сводятся. [c.184]
Важную роль в правильном выборе параметрического класса допустимых решений играет предварительный анализ геометрической структуры совокупности исходных данных и в первую очередь анализ геометрии парных корреляционных полей, включающий в себя, в частности, учет и формализацию гладких свойств искомой функции регрессии, использование вспомогательных линеаризующих преобразований. [c.207]
В специальной литературе приводятся несколько вариантов набора инструментов качества. Например, в [7, 23] рассматривается семь инструментов качества метод расслоения информации по группам факторов, влияющих на качество процессов, графики, диаграммы Парето, причинно-следственные диаграммы (диаграмма Исикавы), гистограммы, диаграммы разброса, контрольные карты и контрольные листки. В этом же источнике приводятся семь дополнительных инструментов качества диаграммы сродства (сходства), диаграммы зависимостей, системные (древовидные) диаграммы, матричные диаграммы, сетевые графы, диаграммы планирования процессов, метод анализа матричных данных. В [23] приведены девять инструментов качества 1) построение схемы процесса 2) контрольный листок 3) мозговая атака 4) диаграмма Парето 5) причинно-следственная диаграмма (диаграмма Исикавы) 6) временной ряд 7) гистограмма 8) диаграмма рассеяния (корреляционное поле) 9) контрольная карта. [c.470]
