Сети нейронов высоких порядков Полиномиальная регрессия [c.202]
Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени в отдельных случаях — полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку. [c.63]
Хотя коэффициент детерминации по модели, параметры которой были рассчитаны обычным МНК, несколько выше, однако стандартные ошибки коэффициентов регрессии в модели, полученной с учетом ограничений на полиномиальную структуру лага, значительно снизились. Кроме того, модель, полученная обычным МНК, обладает более существенным недостатком коэффициенты регрессии при лаговых переменных этой модели xt и х, 3 нельзя считать статистически значимыми. [c.305]
Метод структурной минимизации риска может быть использован для восстановления регрессии в различных классах функций. Применим его для построения полиномиальной регрессии. [c.196]
| Рис. 6.13. Истинная кусочно-линейная регрессия (—) и ее полиномиальная аппроксимация, полученная с помощью алгоритма структурной минимизации критерия адекватности | 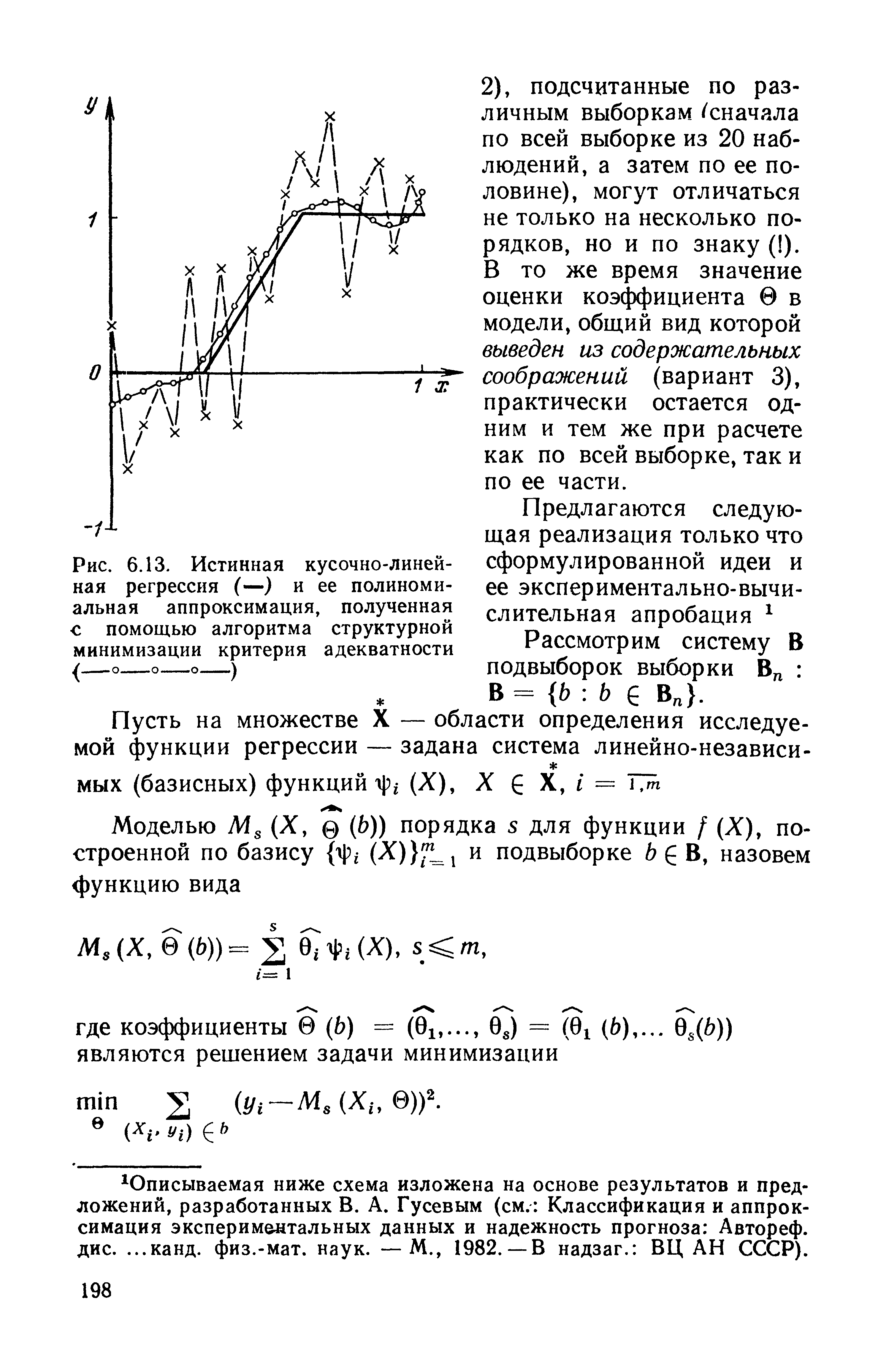 |
Когда истинный порядок полиномиальной регрессии не известен, то оценка параметров модели (7.18) проводится каж- [c.211]
Такая модель может быть получена, например, в полиномиальной регрессии при переходе к ортонормированной системе полиномов. В общей модели регрессии ортонормированными [c.262]
Полиномиальная регрессия. Рассмотрим случай скалярного (т. е. одномерного, р = 1) предиктора к, и пусть искомая функция регрессии / (х) принадлежит классу алгебраических полиномов степени т, т. е. [c.349]
Погрешность решения системы линейных уравнений 273 Полиномиальная регрессия 211, 349 Полиномы Чебышева 211, 327 Порядковые (ординальные) переменные 23, 99 [c.474]
Программа полиномиальной регрессии [c.180]
Многообразие и сложность экономических процессов предопределяет многообразие моделей, используемых для эконометрического анализа. С другой стороны, это существенно усложняет процесс нахождения максимально адекватной формулы зависимости. Для случая парной регрессии подбор модели обычно осуществляется по виду расположения наблюдаемых точек на корреляционном поле. Однако нередки ситуации, когда расположение точек приблизительно соответствует нескольким функциям и необходимо из них выявить наилучшую. Например, криволинейные зависимости могут аппроксимироваться полиномиальной, показательной, степенной, логарифмической функциями. Еще более неоднозначна ситуация для множествен- [c.189]
Здесь (11.5) — регрессия без ограничений, а (11.7) — регрессия с ограничениями.) В том случае, если значение F достаточно мало (меньше критического значения. F-статистики), модель полиномиальных лагов адекватна данным. Как обычно, при прочих равных условиях, надо выбирать модель с наименьшим количеством параметров. [c.267]
Полиномиальная регрессия выбирается, когда имеет место немонотонная зависимость между X и Y. Если на корреляционном поле есть только одна точка максимума или минимума, то выбирается квадратичная регрессия. [c.73]
Полиномиальная регрессия не может быть сведена с помощью замены переменных к линейной регрессии, поэтому для квадратичной модели надо пользоваться уравнениями (5.24). [c.74]
Построение линейных моделей. Осуществляется с использованием многомерной пошаговой регрессии и линейного варианта полиномиального алгоритма МГУА. Из полученных моделей была выбрана лучшая модель [c.322]
Пример. Дадим прогноз валового национального продукта США на 1979—1980 гг. в текущих ценах по данным4 за предшествующие 50 лет. Используем систему STADIA 5.O. Используя блок статистики системы и процедуру Простая регрессия (тренд) , получим оценки полиномиальной модели. Точность модели повышалась, пока степень полинома не достигла пятой [c.102]
IFPS имеет встроенный набор математических и статистических функций, в частности, функции линейной регрессии, линейной интерполяции, полиномиальной автокорреляции и скользящего среднего [c.314]
При сложных полиномиальных функциях с большим числом факторов необходимо помнить, что каждый параметр преобразованной функции является средней величиной, которая должна быть подсчитана по достаточному числу наблюдений. Если число наблюдений невелико, что, как правило, имеет место в эконометрике, то увеличение числа параметров функции приведет к их статистической незначимости и соответственно потребует упрощения вида функции. Если один и тот же фактор вводится в регрессию в разных степенях, то каждая степень рассматривается как самостоятельный фактор. Так, если модель имеет вид полинома второго порядка [c.104]
Рассмотрим общую модель с распределенным лагом, имеющую конечную максимальную величину лага /, которая описывается соотношением (7.3). Предположим, было установлено, что в исследуемой модели имеет место полиномиальная структура лага, т. е. зависимость коэффициентов регрессии Ь-, от величины лага описывается полиномом k-Pi степени. Частным случаем полиномиальной структуры лага является линейная модель (рис. 7.1 а)). Примерами лагов, образующих полином 2-й степени, явля- [c.298]
Некоторые вспомогательные преобразования, линеаризующие исследуемую парную зависимость. Часто при рассмотрении парных корреляционных полей ни линейная, ни полиномиальная регрессия не дают желаемой точности приближения. В этих случаях приходится обращаться к другим видам зависимостей гиперболической, степенной, показательной и др. Покажем, что в ряде ситуаций эти зависимости оказываются не менее удобными, чем линейная, поскольку легко к ней сводятся. [c.184]
В общем случае ответов на эти вопросы пока нет. Однако ориентиром может стать изучение модельных ситуаций. В частности, воспользуемся моделью засорения Шурыгина [14, п. 6.1.11]. В качестве основного распределения возьмем модель нормальной полиномиальной регрессии степени р, когда [c.221]
Случаи линейной (по предикторным переменным) и полиномиальной регрессии. Воспользуемся полученными в предыдущем пункте рекомендациями для анализа точности моделей линейной и полиномиальной регрессии. Нас будет интересовать, в частности, конкретизация формул (11.18 ) и (11.19) в этих случаях. [c.345]
Регрессионный анализ с помощью функции может выполнять простой, полиномиальный и анализ. Результат включает линейное уравнение регрессии, таблицу коэффициентов скорректированный таблицу ANOVA, таблицу соответствий и остатков, которые дали необычные наблюдения. Другие доступные характеристики включают ступенчатую регрессию, наилучшие подмножества, график подогнанной линии регрессии и диаграммы остатков. [c.675]
С учетом пяти форм полиномиальных уравнении тренда, можно получить девять форм уравнений регрессии. Речь идет только о трендах, т. е. об однофакторных моделях. (В Ex el, как известно, имеется также мощный инструментарий линейного многофакторного коррешвдионно-регресснонного моделирования.) [c.155]
