Изучение тенденций развития динамики себестоимости добычи нефти, статей затрат и факторов, оказывающих решающее влияние на уровень и динамику этих показателей, свидетельствует о том, что моделирование их можно выполнить при использовании прежде всего таких функций времени (трендов), которые решаются методом наименьших квадратов (линейные, параболические, показательные, логарифмические), а также с применением методов экспоненциального сглаживания, гармонических весов и т. д. [c.102]
В логарифмической форме функция (2.9) имеет вид [c.102]
Степенную производственную функцию (3.1) часто представляют в более удобном логарифмическом виде, эквивалентном (3.1) при а ,>0 U=l,. .., п) [c.84]
Эластичность выпуска по /-му ресурсу легко получить из логарифмического представления степенной функции [c.84]
Здесь а,-, р , с,- — параметры, оцениваемые на основе экономической статистики. Степенную функцию спроса можно представить в логарифмическом виде [c.125]
Наиболее часто применяемыми в экономике функциями являются элементарные линейная, логарифмическая, степенная, экспонента и т.д., а также различные их комбинации (см. таблицу ниже). [c.220]
Модель позволяет увидеть, что в странах с рыночной экономикой главным фактором роста производства является его прибыльность, которая в данном случае определяет темпы роста на 72,8%. Наряду с полиномами используются степенные, логарифмические, тригонометрические функции и их комбинации. Во многих статистических пакетах пользователю предоставляется широкий выбор нелинейных моделей. [c.91]
По виду страхования №2 показатель убыточности развивается по логарифмической функции, поэтому расчеты имеют следующий вид [c.415]
| Рис. 10.4. Выравнивание показателя убыточности по логарифмической функции | 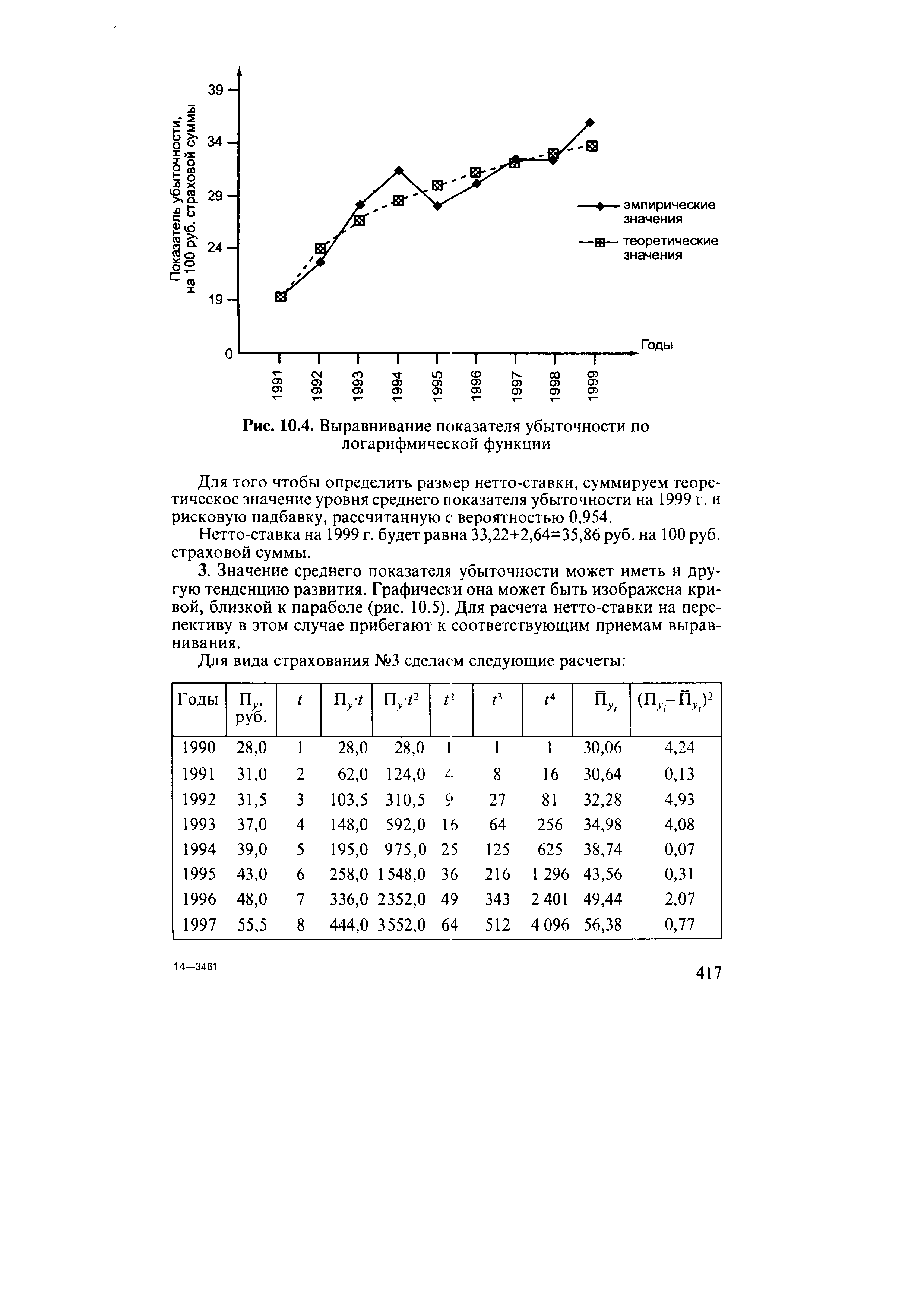 |
Корреляционная зависимость в отличие от функциональной является неполной, проявляется лишь в среднем и только в массе наблюдений. При корреляционной связи изменению аргумента соответствует несколько значений функций. В зависимости от количества отобранных факторов различают парные и многофакторные модели различного вида линейные, степенные, логарифмические. В практике прогнозирования наибольшее распространение получили линейные модели вида [c.129]
Например, для А/ СЯ(1)-модели логарифмическая функция правдоподобия имеет вид [c.217]
| Рис. 4.9. Трендовая модель тенденции развития рынка по логарифмической функции | 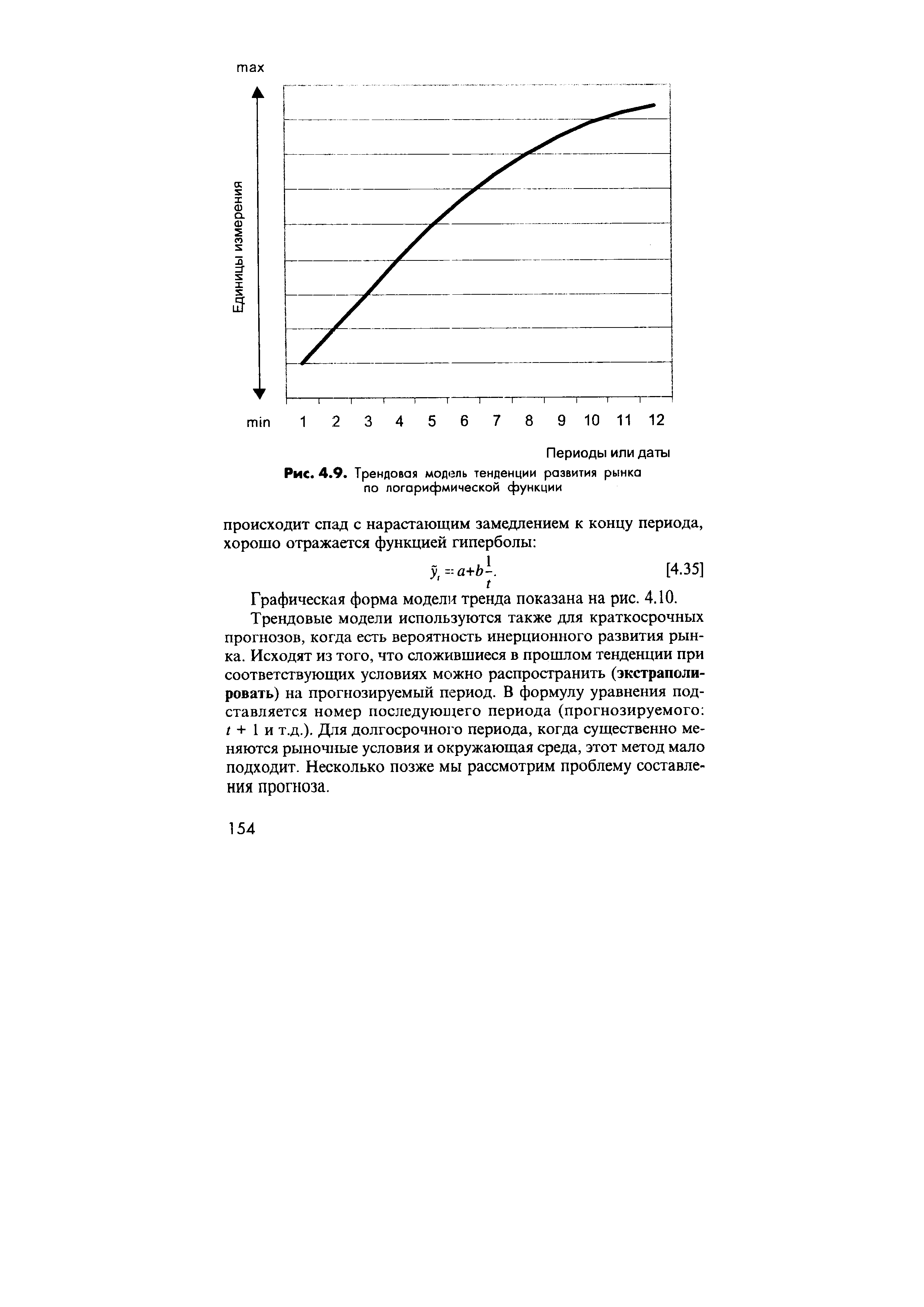 |
Перед тем как рынок станет реальностью, он существует в скрытой форме. Скрытый рынок состоит из покупателей с одинаковыми потребностями или желанием получить нечто, еще не существующее. Например, веками люди мечтали иметь средство, позволяющее производить вычисления быстрее, чем с помощью ручки или карандаша. До недавнего прошлого для этой цели служили счеты, логарифмическая линейка или громоздкий арифмометр. Предположим, предприниматель выявил эту потребность и придумал техническое устройство в виде небольшого электронного калькулятора. Теперь он должен определить свойства своего товара, включая размер и количество математических функций, которые он будет выполнять. [c.441]
Часто прогнозирование проводится на базе динамических (или временных) рядов. В этом случае для определения ожидаемого значения показателя в будущем в первую очередь строят график исходного динамического ряда и путем сравнения его с графиком известных функций отбирают наиболее подходящую (линейная, парабола, логарифмическая, степенная, показательная, гиперболическая и др.), охватывающую исходные данные. Экономические показатели как члены динамического ряда содержат в себе результат [c.89]
Аналогичными расчетами (здесь не приводятся) установлено, что средний квадрат отклонения между нашими значениями переменных в случае рассмотрения их по типу гиперболы составит о = 1,299, в случае логарифмической показательной функции о = 1,487 и в случае параболы 2-го порядка а составит многие сотни единиц. Следовательно, расчетная величина нашей зависимой переменной имеет наименьшее среднее отклонение от фактической при прямой связи. [c.49]
Расчеты дисперсии ряда (а2) показали, что наименьшее значение среднего квадрата отклонения переменной (у") от ее среднего значения (у"х) имеет гиперболическая связь между рассматриваемыми нами величинами потребления отраслью керосина и ее валовой продукции. Так, о при гиперболе составляет 0,0942, при прямой линии — 1,4018, при показательной логарифмической функции — 62,82 и при параболе — свыше тысячи. [c.52]
| Рис. 7. Функция плотности логарифмически-нормального закона. | 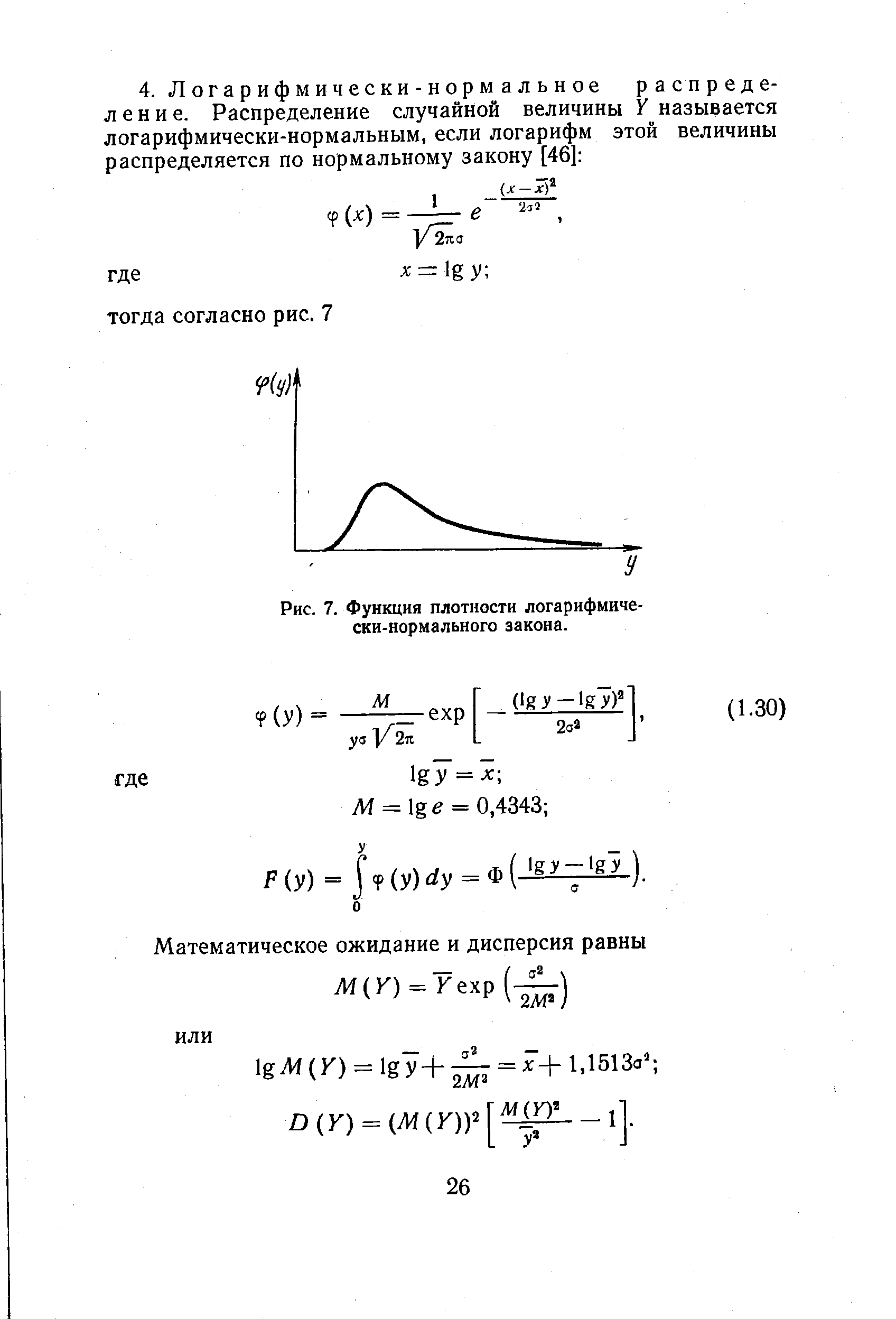 |
Вопрос о теории полезности поднимается в книге из-за того, что сторонников максимизации среднего геометрического часто критикуют за то, что они способны максимизировать лишь случай логарифмической (In x) полезности. То есть они стремятся максимизировать только богатство, а не удовлетворенность инвестора. В этой книге мы попытаемся показать, что максимизацию среднего геометрического можно применять при любой функции полезности. Поэтому теперь нам придется обсудить теорию полезности в общем плане, на уровне основных понятий. [c.112]
Теорию полезности часто критикуют за то, что она трактует поведение инвестора в отрыве от практики. К сожалению, большинство этих нападок исходит от людей, принявших априорное предположение, что все функции полезности инвестора являются логарифмическими, то есть что они нацелены на максимизацию капитала. Не являясь большим сторонником теории полезности, я принимаю ее из-за отсутствия лучшего объяснения предпочтений инвестора. Вместе с тем, я твердо убежден, что если функция полезности инвестора отличается от In x, то на рынках и в инвестировании в целом ему не место — ваше поло- [c.112]
На рис. 2.4 изображены три основных типа функций предпочтения полезности в зависимости от U"(x), или степени неприятия риска инвестора. Функция предпочтения полезности, равная In x, демонстрирует нейтральное отношение к риску. Инвестор индифферентен к справедливой азартной игре. Для логарифмической функции предпочтения полезности вторая производная будет равна — х г. [c.115]
В случае логарифмической функции предпочтения полезности имеет место понижающееся абсолютное неприятие риска. Для In х имеем [c.116]
Зачастую критерий среднего геометрического критикуют за его нацеленность исключительно на максимизацию капитала и за то, что он максимизирует полезность только для логарифмической функции. [c.125]
На деле же, тот, кто не придерживается логарифмической функции предпочтения полезности, всегда может максимизировать полезность во многом подобно тому, как мы максимизируем капитал с помощью оптимального /, за тем исключением, что для каждого периода владения будет свое значение оптимального / То есть если чья-то функция предпочтения полезности отличается от In x (максимизация капитала), то его оптимальное/для максимизации (асимптотической) полезности будет переменным, в то время как его оптимальное / для максимизации капитала будет постоянным. Другими словами, если, зарабатывая больше денег, вы следуете такой полезности, что готовы рисковать все меньше, то ваше оптимальное/будет уменьшаться с завершением каждого периода владения. [c.125]
Впрочем, мы предупредили этих читателей, что им все равно придется оплатить (деньгами) издержки своего субоптимального положения в (п + 1)-мерном пространстве рычагов максимизации капитала. Вновь повторю, что это так потому, что безотносительно к вашей кривой предпочтения полезности, вы находитесь где-то на плоскости (см. рис. 1.2) для одной игры и где-то в (и + 1)-мерном пространстве рычагов для нескольких одновременных игр. Вы пользуетесь преимуществами, точно так же, как оплачиваете издержки этого вне всякой связи с вашей функцией предпочтения полезности. В идеале, ваша функция предпочтения полезности должна быть логарифмической. [c.129]
| Рис. 22. Функция распределения вероятности квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое игровой модели гидродинамической турбулентности, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, что прямая линия, которая помогает глазу, квалифицируется, как очевидное показательное распределение. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на краю, выше экстраполяции прямой линии. Источник [252]. | ![Рис. 22. <a href="/info/21981">Функция распределения вероятности</a> квадрата скорости жидкости, нормализованная к ее среднему времени, в одиннадцатом слое игровой модели гидродинамической турбулентности, обсуждаемой в тексте. Вертикальная ось имеет такой логарифмический масштаб, что прямая линия, которая помогает глазу, квалифицируется, как очевидное <a href="/info/5302">показательное распределение</a>. Обратите внимание на появление чрезвычайно редких и больших взрывов скоростей на краю, выше экстраполяции прямой линии. Источник [252].](/pic1/205196012179108108119160056012034002236089221065.png) |
| Рис. 23. Функция распределения вероятности квадрата скорости как на Рис. 22, но для гораздо более длинного ряда времени, чтобы хвост распределений для очень больших флуктуации был намного лучше ограничен. Гипотеза о том, что не существует "выбросов" здесь проверяется "разрушением" распределения для трех показанных слоев. В то время, как это имеет успех для маленьких колебаний, хвосты распределений для больших событий весьма различны, указывая, что экстремальные колебания принадлежат к собственному классу и, следовательно, "выбросы". Вертикальная ось снова в логарифмическом масштабе. Источник [252]. | ![Рис. 23. <a href="/info/21981">Функция распределения вероятности</a> квадрата скорости как на Рис. 22, но для гораздо более длинного <a href="/info/4684">ряда времени</a>, чтобы хвост распределений для очень больших флуктуации был намного лучше ограничен. Гипотеза о том, что не существует "выбросов" здесь проверяется "разрушением" распределения для трех показанных слоев. В то время, как это имеет успех для маленьких колебаний, хвосты распределений для больших событий весьма различны, указывая, что экстремальные колебания принадлежат к собственному классу и, следовательно, "выбросы". Вертикальная ось снова в логарифмическом масштабе. Источник [252].](/pic1/151255070046029077102042074146191012187176133187.png) |
| Рис. 88. Те же данные, что и на Рис. 87. Модуль yi (t) "сниженной цены" показан как функция t -t, где t =4 в двойных логарифмических координатах, таких что линейная огибающая показывает дивергенцию степенной зависимости (t -t 1 5. Наклон пунктирной линии равен -1,5. Также обратите внимание, что осцилляции примерно равноотстоят по переменной ln(t -t), что напоминает логопериодическое поведение ускоряющихся осцилляции при приближении к сингулярности. Источник [205]. | ![Рис. 88. Те же данные, что и на Рис. 87. Модуль yi (t) "<a href="/info/78047">сниженной цены</a>" показан как функция t -t, где t =4 в двойных логарифмических координатах, таких что линейная огибающая показывает дивергенцию степенной зависимости (t -t 1 5. Наклон пунктирной линии равен -1,5. Также обратите внимание, что осцилляции примерно равноотстоят по переменной ln(t -t), что напоминает логопериодическое поведение ускоряющихся осцилляции при приближении к сингулярности. Источник [205].](/pic1/214161157167241117202114127217064234003098219063.png) |
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ [derivation] — операция определения производной рассматриваемой функции. Напр., производная линейной функции (Ьх + а У = Ъ, т.е. является константой производная степенной функции [х") -= ах" 1 (>0), т.е. дифференцирование степенной функции уменьшает ее степень на единицу или дифференцирование логарифмической функции (logoJt) = 1/х log/ (0 < а Ф 1 х>0), в частности (In x) = Их. Для Д.ф., представляющей собой комбинацию элементарных функций, применяются специальные правила напр., производная суммы (разности) функций равна сумме (разности) производных этих функций, постоянный множитель выносится за знак производной для дифференцирования произведения двух функций вычисляется сумма из двух произведений (производная первой функции на вторую функцию, плюс первая функция на производную второй функции — (u(x)v(x)) = u (x)v(x) + + u(x)v(x) ). Соответственно, существуют правила дифференцирования сложной функции, частного двух функций, обратной функции, логарифмических функций, правила вычисления производных высших порядков, а также правила Д.ф. многих переменных. [c.92]
Проведем предельные переходы. Применяя при р -> О правило Лопиталя к функции (2.10), получаем логарифмическую формулу функции Кобба — Дугласа [c.103]
Вид кривой жизненного цикла потребности и ее теоретическая интерпретация в каждом конкретном случае могут быть различными. Наиболее приемлемыми функциями, описывающими поведение графика потребности в этот период могут быть кривая Гомпертца и логистическая кривая. Но в отдельных случаях с достаточной степенью точности изменение потребности может быть аппроксимировано модифицированной экспонентой, логарифмической и обратнологарифмической зависимостями. При этом идентификация кривой жизненного цикла потребности по выбранной аналитической зависимости производится с использованием математического инструментария, в частности, основных положений теории математической статистики. [c.136]
Используя элементарные свойства логарифмической функции ( = lnexp Ina + lnb = nab), преобразуем данное выражение к виду [c.118]
Важным способом стимулирования корпоративного воображения является отказ от традиционного уровня цен продукта с определенными функциями и характеристиками. Например, фирмы Sony и JV задались идеей сконструировать видеомагнитофоны, стоившие ранее 25000 фунтов стерлингов, таким образом, чтобы их цена не превышала 300 фунтов, и предоставили своим инженерам свободу действий для воплощения мечты в реальность. Главное - отбросить идею о том, что единственной отправной точкой при разработке нового продукта является существующий продукт. Классический" пример электронный калькулятор, заменивший логарифмическую линейку. [c.126]
Мы немного познакомились с математикой нормального и логарифмически нормального распределения и теперь посмотрим, как находить оптимальное f по нормально распределенным результатам. Формула Келли является примером параметрического оптимального f, где f является функцией двух параметров. В формуле Келли вводные параметры — это процент выигрышных ставок и отношение выигрыша к проигрышу. Однако формула Келли даст вам оптимальное f только тогда, когда возможные результаты имеют бернуллиево распределение. Другими словами, формула Келли даст правильное оптимальное f, когда есть только два возможных результата, в противном случае, как, например, в нормально распределенных результатах, формула Келли не даст вам правильное оптимальное f2. [c.102]
| Рис. 38. Двумерные (линии уровня) и трехмерные графики распределения ценовых приращений в интервале 200 торговых дней, с центром 19 октября 1987 (соответствует О абсциссы). Масштаб плотности вероятности (ось Z) поверхностного участка логарифмический, что обеспечивает для прямого затухания экспоненциальное распределение. График изоквант (линий, на которых логарифм функции плотности вероятности принимает одинаковое значение) на верхней грани куба кодируется яркостью. Самая яркая область контурного участка соответствует наиболее вероятному значению. Символ R означает return (исход или приращение). Источник [267]. | ![Рис. 38. Двумерные (линии уровня) и <a href="/info/68612">трехмерные графики</a> <a href="/info/186383">распределения ценовых</a> приращений в интервале 200 торговых дней, с центром 19 октября 1987 (соответствует О абсциссы). Масштаб <a href="/info/57048">плотности вероятности</a> (ось Z) поверхностного участка логарифмический, что обеспечивает для прямого затухания <a href="/info/5307">экспоненциальное распределение</a>. График изоквант (линий, на которых логарифм <a href="/info/4084">функции плотности вероятности</a> принимает одинаковое значение) на верхней грани куба кодируется яркостью. Самая яркая область контурного участка соответствует наиболее вероятному значению. Символ R означает return (исход или приращение). Источник [267].](/pic1/138154024202029233183212150171108162190023120105.png) |
Рис. 81 иллюстрирует зависимость размерности фрактальной структуры троичного канторова множества как функцию уровня разрешения. Данная величина называется корреляцией и подсчитывает число пар точек в канторовом множестве, отделенных друг от друга расстоянием меньшим, чем разрешение. В таком двойном логарифмическом представлении наклон линии должен быть равен действительной фрактальной размерности d=ln2/ln3=0,6309..., поскольку корреляционная функция растет согласно разрешению, возведенному в степень d. Здесь мы снова видим логопериодические осцилляции, осложняющие линейный в среднем, тренд с положительным, в среднем, наклоном. Данные логопериодические структуры отражают дискретную масштабную инвариантность канторова множества. [c.208]
Смотреть страницы где упоминается термин Функция логарифмическая
: [c.602] [c.263] [c.106] [c.51] [c.126] [c.55] [c.87] [c.88] [c.212]Эконометрика начальный курс (2004) -- [ c.246 , c.253 ]
