Самыми подходящими функциями в качестве тренда являются многочлены, показательная функция и логистическая кривая . [c.68]
Для построения прогнозных моделей используют различные группы типичных функций, из которых выбирают характерную для исследуемого объекта. Так, в первую группу входят линейные функции, во вторую — чистые экспоненты и с насыщением, т. е. логистические или S-образные кривые, в третью — кривые, характеризующие удвоенный экспоненциальный рост с последующим насыщением, в четвертую — кривые, характеризующиеся сначала медленным, а затем резким экспоненциальным ростом с последующим насыщением. [c.23]
Изменение во времени характерных параметров для большинства изделий микроэлектроники (степень интеграции, быстродействие, объем памяти и др.) происходит по экспоненциальным кривым. Поэтому для прогнозирования широко используют логистические кривые, которые описывают ускоренное развитие до определенного момента времени (до точки перегиба) с последующим замедлением роста под влиянием ограничивающих (в основном технологических) факторов и переходом к насыщению. [c.23]
Для моделирования уровней процентных ставок в статистике используют различные типы уравнений, в том числе полиномы разных степеней, экспоненты, логистические кривые и прочие виды функций. [c.619]
Если ряд динамики имеет тенденцию к быстрому развитию показателя вначале периода и спаду к концу периода, то целесообразно применять логистические кривые. [c.620]
Для отображения основной тенденции развития явлений во времени применяются различные уравнения, полиномы разной степени, экспоненты, логистические кривые и другие функции. [c.80]
Логистическая кривая имеет вид положенной на бок латинской буквы S. Она описывает случай когда при увеличении фактора X отклик 7 изменяется (снижается при а > О или растет при а < О ) в пределах от 0 до 1. При этом изменения происходят при х < b с увеличивающейся скоростью и при X > b с уменьшающейся скоростью. Преобразование данных [c.129]
Такое изолированное положение равновесия нелинейной системы называется точечным аттрактором. Разумеется, если цена постоянно будет испытывать случайные изменения, точное равновесие никогда не будет достигнуто. На рис. 3.4 показана логистическая кривая для другого набора параметров с = 1, l = -4, с2 = 4. . [c.76]
| Рис. 3.2. Логистическая кривая квадратичная обратная связь | 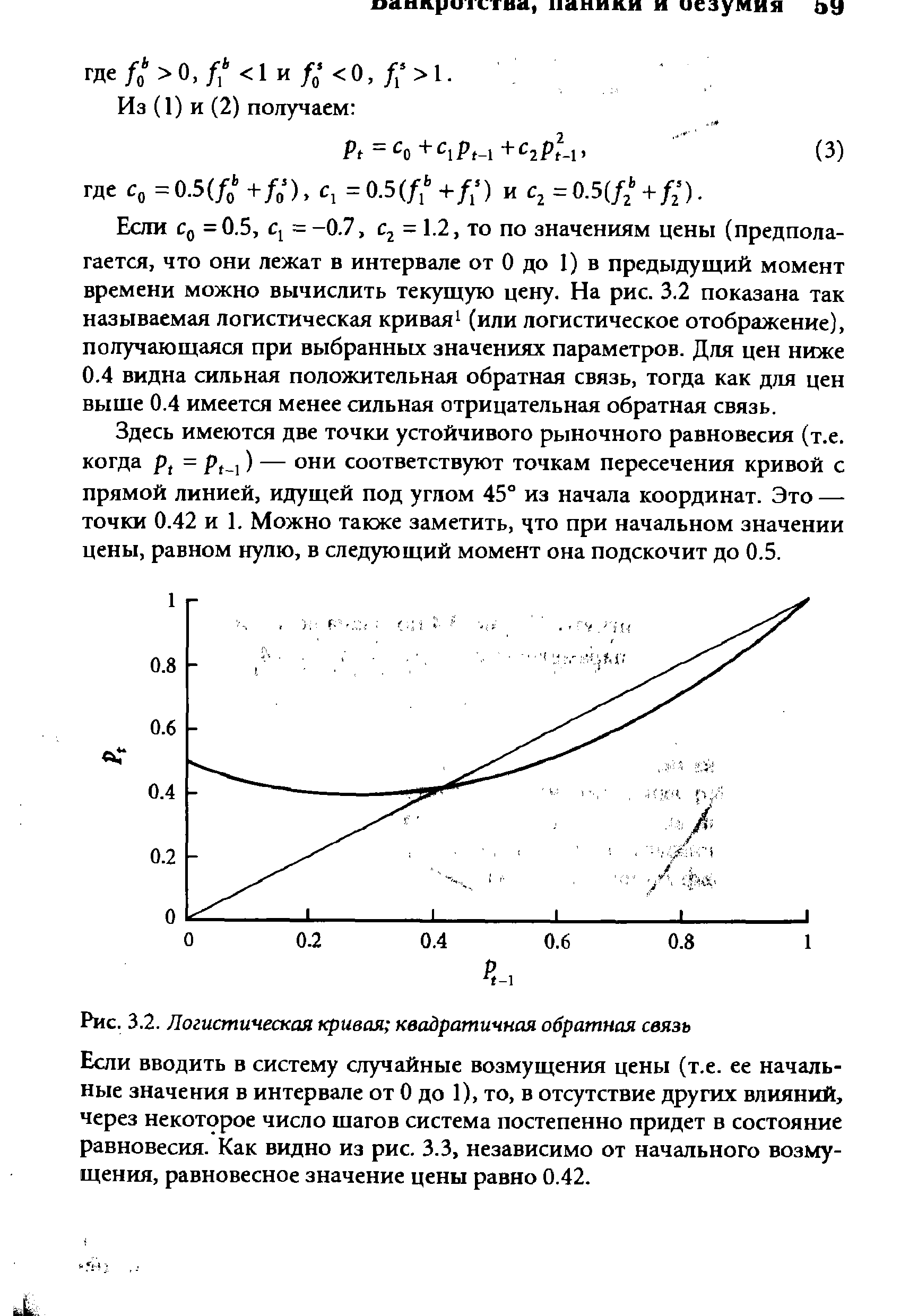 |
Общий вид логистической кривой [c.21]
Логистическая (S-образная) кривая, описывающая жизненный [c.21]
Зависимость Y=Y(X) представляет собой логистическую кривую [c.151]
Эффект от сокращения цикла СОНТ может быть приближенно рассчитан следующим путем. Как отмечалось ранее, рост выпуска продукции на этапе освоения по календарным отрезкам времени происходит по логистической кривой. Рост выпуска продукции в зависимости от времени (цикла), прошедшего с начала освоения (рис. 10.5), будет различен для разной длительности циклов освоения. При обычном освоении, т. е. без осуществления мероприятий, направленных на ускорение освоения, длительность цикла будет иметь нормальную продолжительность. При ускоренном освоении производства длительность цикла будет иметь сокращенную продолжительность. [c.101]
Логистическая кривая имеет форму латинской буквы s положенной на бок, отчего еще называется эсобраэной кривой. Она имеет два перегиба от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста посреди периода к замедляющемуся (выпуклость). Она подходит для отображения развития в течение длительного периода, проходящего все фазы, например процесса насыщения потребителей каким-то новым товаром, скажем, телевизорами сначала медленный, но все ускоряющийся рост доли семей, [c.325]
Если закон циклического развития воздействует как на внешнюю, так и на внутреннюю среду предприятия, определяя в целом развитие совокупности систем, то другие законы определяют отдельные участки S- образной кривой развития производственных систем. Например, законы перехода к малооперационным процессам, возрастания необходимого разнообразия и сложности систем описывают поведение систем в области, близкой к логистическому участку кривой (продляя в ряде случаев линейный участок), закон убывающей эффективности эволюционного совершенствования систем характеризует поведение систем на логистическом участке кривой. [c.93]
Вид кривой жизненного цикла потребности и ее теоретическая интерпретация в каждом конкретном случае могут быть различными. Наиболее приемлемыми функциями, описывающими поведение графика потребности в этот период могут быть кривая Гомпертца и логистическая кривая. Но в отдельных случаях с достаточной степенью точности изменение потребности может быть аппроксимировано модифицированной экспонентой, логарифмической и обратнологарифмической зависимостями. При этом идентификация кривой жизненного цикла потребности по выбранной аналитической зависимости производится с использованием математического инструментария, в частности, основных положений теории математической статистики. [c.136]
Методы математической статистики, теории очередей, экстраполяции (логистических и огибающих кривых), моделирования, экспертных оценок (мозговая атака, комиссий и т.д.), межстрано-вое сопоставление и др. [c.130]
