Современный рынок дает все больше признаков для его рассмотрения как нелинейной системы, которая все значительнее проявляет себя в драматических обвалах рынка при отсутствии существенных [c.113]
Наука - большая, открытая, самоорганизующаяся нелинейная система, которая может существовать только за счет обмена информацией внутри себя и с внешней средой. Ее подсистемы динамичны, неустойчивы и неравновесны. При этом информационные потоки играют не только решающую, но и организующую роль. Информация воспринимается, потребляется, обрабатывается, сохраняется, возвращается обратно. Внешняя среда может быть доброжелательной, либо настроена враждебно. Поэтому необходимо выявлять неблагоприятные проявления и упреждать их. [c.166]
Когда нам не удаются успешные предсказания, то следующим, естественным, шагом будет поиск большей информации, которая должна улучшить результаты. В нелинейных системах накопление большего количества информации часто не только является необязательным, но и часто совершенно бесполезным делом. Сложное поведение возникает из простых повторений и нелинейной обратной связи. [c.164]
| Рис. 3.3. Точечный аттрактор простейшей нелинейной системы | 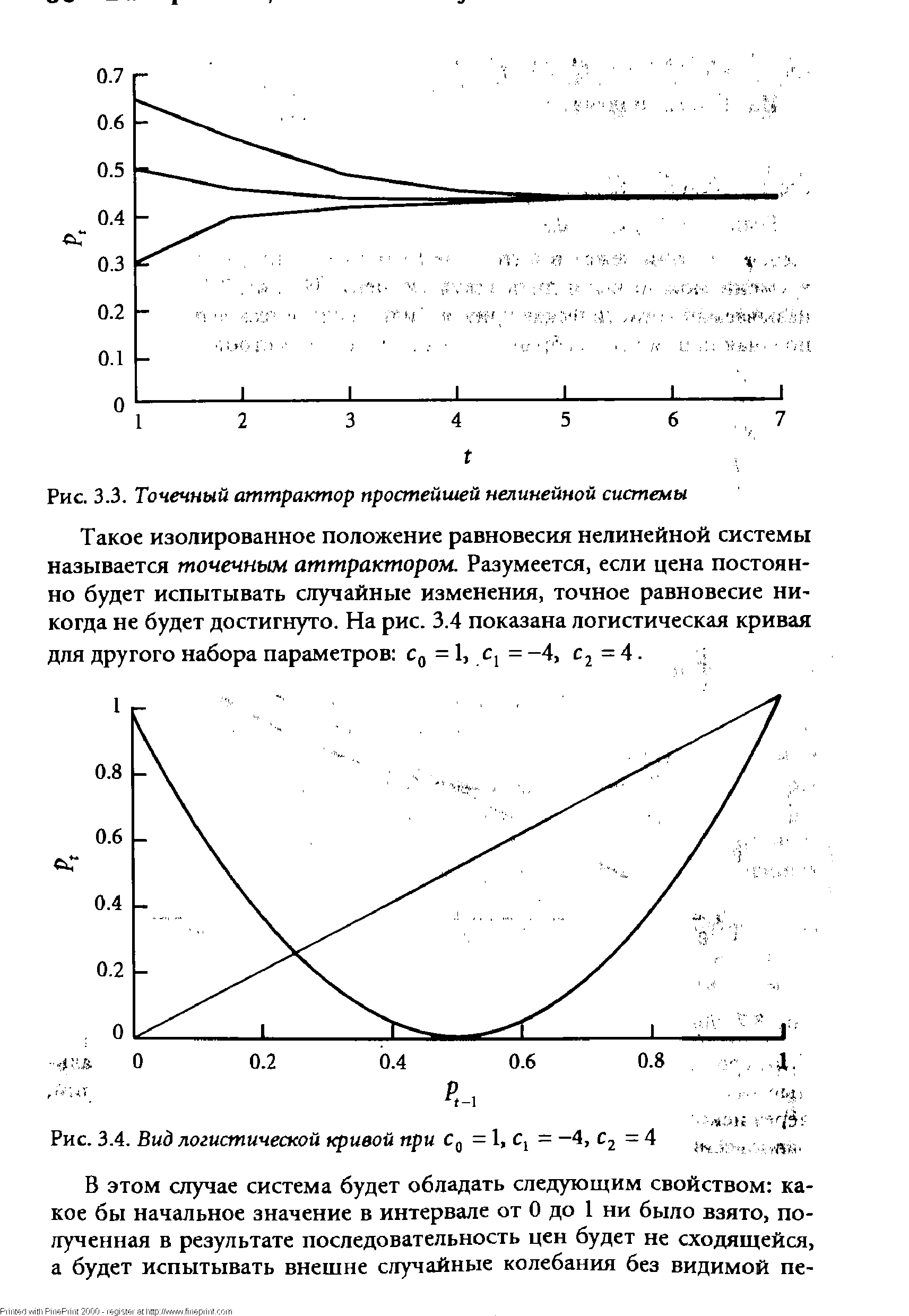 |
При анализе взаимодействия людей наибольший интерес представляют нелинейные системы, в которых интегральный эффект оказывается больше суммы индивидуальных результатов. Примером такой системы является групповое обслуживание оборудования. Как было показано в разделе 9.3, на основе сравнения норм обслуживания можно оценить рост продуктивности труда при переходе от индивидуального обслуживания станков к коллективному. В данной задаче рост продуктивности достигается за счет лучшего использования фондов времени рабочих. [c.295]
Точное решение задачи можно найти, зная структуру (13). Оно определяется двумя параметрами tlf t2, вычисление которых требует решения некоторой нелинейной системы уравнений. Мы ограничимся здесь только общими указаниями, не доводя дела до окончательных формул. Итак, пусть заданы числа ti, t2. [c.300]
Хаотические системы обычно являются нелинейными системами с обратной связью. Они подвержены беспорядочному поведению, усилению событий и разрывам. Дня того чтобы система считалась хаотичной, должны выполняться два требования (1) существование фрактальной размерности и (2) характеристика, называемая чувствительной зависимостью от начальных условий. Более полное обсуждение этих характеристик приводилось в моей предыдущей книге, но было бы целесообразно провести основной обзор, поскольку дробный шум и шумовой хаос трудно отличить друг от друга, особенно при исследовании эмпирических данных. [c.228]
Динамическая система. Система уравнений, где выход одного уравнения является частью входа другого. Простым примером динамической системы может служить последовательность линейных систем уравнений. Нелинейные системы уравнений являются нелинейными динамическими системами. [c.286]
Эта модель не реалистична, она предполагает, например, что давление продавцов прямо соотносится со скоростью роста покупательского спроса. Однако она показывает, как сложные результаты могут порождаться даже в простой нелинейной системе. Легко представить себе уровень сложности большой нелинейной системы, такой например, как погода [c.22]
Причина здесь в том, что дневные данные образуют только один цикл, а месячные — десять циклов. Из этого следует, что надо быть очень внимательным к стандартам, которые мы применяем в нелинейном анализе. Обычный метод привлечения большого количества данных помогает в анализе только тогда, когда исследуется IID (независимые идентично распределенные данные). Тогда время не имеет значения — в противоположность количеству наблюдений. Однако нелинейные системы имеют стрелу времени. Время не может быть повернуто вспять, и длина временного периода более важна, чем разрешение данных. Фактически увеличение разрешения часто делает анализ более затруднительным, но не повышает значимость результатов. [c.142]
Эмпирический анализ никогда не бывает совершенным — он всегда содержит нечеткости. Аккуратные, упорядоченные странные аттракторы теории редко встречаются в реальной жизни. Тем не менее мы можем установить факт, что перед нами нелинейная динамическая система. Если же мы приходим к такому выводу, то можем создать модели из уравнений с целью установления закономерностей движения. Доказательство нелинейности системы — дело нелегкое, но осуществимое. Оно требует терпения и готовности к проверке различных идей, какими бы странными они ни казались. [c.178]
В экономических и технологических исследованиях при фиксированном значении регрессора X часто рассматривается многомерный отклик Y = Чг/ (X)Q + е, где Y — (/X 1) -вектор наблюдений при значении регрессора X, Чг — известная (/ X р)-матричная функция X, в — (рх 1)-вектор неизвестных параметров, а е — (/X 1)-вектор ошибок N (О, V), где V — неизвестная положительно определенная (/ X /)-матрица. Оценка вектора в многомерной регрессии проводится одновременно с оценкой матрицы V путем итеративного решения нелинейной системы уравнений. Разработаны устойчивые методы оценки многомерной регрессии. Многомерная регрессия может использоваться при описании многомерных распределений. [c.250]
Пусть Dk — мнк-оценки параметров этой линейной регрессии. В качестве начальных приближений примем решение нелинейной системы уравнений относительно 9Ь. .., Эш [c.316]
Сложность и высокая размерность указанной нелинейной системы заставляют принять некоторые упрощающие допущения, не лишающие тем не менее поставленную задачу практического смысла. [c.171]
Это обстоятельство правомерным образом ставит вопрос о том, а не являются ли многие экономические, в том числе и финансовые, ряды в действительности не стохастическими, а хаотическими, т. е. описываемыми детерминистическими нелинейными системами, которые, как известно, могут приводить к эффектам (типа "кластерное " скажем), наблюдаемым при статистическом анализе финансовых данных (см. гл. IV). [c.216]
Вопрос об исследовании действия в динамических задачах (в частности, теория фокусов) обсуждается, по существу, во всех монографиях по классическому вариационному исчислению. Теории собственных колебаний линейных систем посвящено огромное число работ отмстим здесь основополагающий труд Рэлея [203] и монографии (76, 116]. Данное в тексте обобщение принципа Рэлея на нелинейные системы совершенно естественно, однако автору не удалось найти его в литературе. [c.429]
Один из возможных графиков отражает нулевой штраф вплоть до некоего критического уровня, а затем свыше его бесконечно большой, что делает уровни загрязнения, превышающие / , невозможными. На деле это регулирование, направленное против загрязнения сверх уровня Р. Таким образом, разграничение между штрафами и предписаниями непросто. Регулирование может рассматриваться как эквивалент ограничивающего случая нелинейной системы штрафов. [c.221]
Проблемы анализа потерь эффективности и распределения налогового бремени. Одним из подходов к построению нелинейной системы акцизов является установление дифференцированных ставок на разные категории товаров одного типа. Однако для части товаров такой дифференцированный подход оказывается невозможным. Поскольку нашей задачей, в конечном счете, является исследование того, насколько требования к вы- [c.116]
Такие сложные нелинейные системы, как экология или организации, характеризуются множественными системами взаимодействия, одновременно упорядоченными к хаотичными. По причине своей внутренней сложности случайные отклонения могут привести к непредсказуемым событиям и взаимоотношениям, которые Отразятся в системе, создавая нестандартные паттерны перемен. Удивительно то, что несмотря на нею свою непредсказуемость, гармоничный порядок всегда возникает из случайности И хаоса. [c.286]
Знаменитый образ - эффект крыла бабочки, когда такое крошечное изменение, как трепетание крыльев бабочки в Пекине, способно изменить погоду в Мексиканском заливе. Или, как выразился автор научных книг Кевин Келли, в сложных нелинейных системах 2 + 2 = яблоки -. [c.289]
Образы и идеи, связанные с другими двумя логиками перемен, которые мы рассмотрим в этой главе, также вносят значительный вклад. Анализ взаимной обусловленности, предлагаемый в следующем разделе, содержит важные образы и представления о природе изменений в нелинейных системах. Исследование противоречий и логики диалектических перемен связано с углубленным изучением напряженности и парадоксов, формирующих процессы самоорганизации, К этому мы сейчас и перейдем. [c.298]
Задача (6.27) — (6.30) не решается аналитически. ввиду нелинейности системы дифференциальных уравнений (6.27) и (6.28). Очевидно, она может быть решена с помощью ЭВМ. Аналогичную задачу, но с другими граничными условиями (6.29) и без условия (6.30), решал приближенным методом Т, Карман и впоследствии численным интегрированием В. Кок-рэн [106]. [c.142]
Динамические модели, в которых условия меняются во времени, подразделяются так же, как и собственно системы, на устойчивые и неустойчивые. Устойчивой считается система, которая, будучи выведена из своего исходного состояния, стремится вернуться к нему. Возмущения, нозникшие в такой системе, со временем затухают и исчезают. В неустойчивых, нелинейных системах (например, промышленных предприятиях) возникшее возмущение часто усиливается, вызывая увеличение значений соответствующих переменных или их колебания с возрастающей амплитудой. Большинство математических моделей, используемых в управлении предприятиями, относится к устойчивым, линейным, статическим или динамическим. [c.305]
Система условий (2.58) — (2.61), при определенных допущениях, может оыть сведена к детерминированной нелинейной системе [43]. Включение указанных условий в оптимизационную задачу с целью единовременного комплексного решения проблемы выбора оптимальных уровней надежности и варианта производственной программы комплекса НПП представляет собой сложную, а ввиду отсутствия в настоящее время эффективных численных методов практически нерешаемую в реальном масштабе времени проблему. Все это позволяет утверждать, что перспективы развития методов динамического моделирования связаны, прежде всего, с развитием методов стохастического программирования. [c.49]
Главная задача инвестора — купить дешевле и продать дороже. Чем выше изменчивость цены актива, тем больше имеется возможностей для проведения выигрышных стратегий торговли, даже с учетом затрат на совершение сделок. К сожалению, то, что кажется простым и очевидным задним числом (ex post), бывает совсем неочевидно наперед (ex ante). Ключевой вопрос здесь заключается в том, можно ли определить направление, величину и волатильность будущих изменений цены актива, экстраполируя имеющиеся прошлые данные. Примеры, разобранные в этой главе, показывают, что адаптивные нелинейные системы могут быть обучены так, чтобы выполнять технический анализ при минимально возможных допущениях. Наш подход к задачам этого типа отличается от других тем, что мы не пытаемся оптимизировать входные данные. На вход сети подавались необработанные данные о ценах акций компании Юнилевер в прошедший период, а сеть была обучена на то, чтобы выдавать ежедневные распоряжения на совершение сделок. [c.211]
Применение нейронных сетей в этой задаче показало, что статическая нелинейная система может быть обучена так, чтобы выполнять технический анализ на начальном уровне. Наш подход отличается от других, известных в этой области, тем, что мы не пытаемся оптимизировать входное множество. На вход сети, предсказывающей направление будущих изменений цен, подавались временные ряды данных в исходном виде. При помощи перемасштабирования данных достигалась инвариантность пространства входов. Затем сеть обучалась с использованием регуляризирующего штрафного члена, ограничивающего положение интерполирующей поверхности, построенной нейронной сетью. Модель выдавала до 54% правильных сигналов. [c.224]
НЕЛИНЕЙНАЯ МОДЕЛЬ [nonlinear model] — экономико-математическая модель, отображающая состояние или функционирование системы (нелинейной системы, стохастической системы) таким образом, что все или некоторые взаимосвязи в ней принимаются нелинейными, т.е. не удовлетворяющими условиям линейности (см. Линейная зависимость, линейность). Основная область применения нелинейных моделей —нелинейное программирование. [c.220]
НЕЛИНЕЙНАЯ СИСТЕМА [nonlinear system] — система, которая характеризуется тем, что все или некоторые зависимости, связывающие входные величины, параметры состояний , выходные величины, являют- [c.220]
См. также Абстрактная система, Адаптирующиеся, адаптивные системы, Большая система, Вероятностная система, Выделение системы, Входы и выходы системы, Детерминированная система, Динамическая система, Дискретная система, Диффузная система, Замкнутая (закрытая) система, Иерархическая структура, Имитационная система, Информационная система, Информационно-развивающаяся система, Кибернетическая система, Координаты системы, Надсис-тема, Нелинейная система, Непрерывная система, Открытая система, Относительно обособленная система, Память системы, Подсистема, Портрет системы, Разомкнутая система, Рефлексная система, Решающая система, Самонастраивающаяся система, Самообучающаяся система, Самоорганизующаяся система, Сложная система, Состояние системы, Статическая система, Стохастическая система, Структура системы, Структуризация системы, Управляющая система, Устойчивость системы, Целенаправленная система, Экономическая система, Функционирование экономической системы. [c.325]
В очень долгосрочной перспективе (периоды более четырех лет для американских рынков акций и облигаций) рынки характеризуются детерминированными нелинейными системами или детерминированным хаосом. Непериодические циклы возникают из взаимозависимости различных рынков капитала между собой, а также из экономики. Рынки, на которых доминируют, прежде всего, трейдеры, при этом связь с флуктуациями основополагающей экономики отсутствует, не будут характеризоваться детерминированным хаосом, даже в долгосрочной перспективе. Вместо этого на них будут доминировать местные AR H-эффекты и глобальные устойчивые характеристики Леви. [c.257]
Применение Д/5-анализа просто и непосредственно, однако требует определенного, достаточно большого количества данных и скрупулезной их обработки. В этой главе мы опишем и представим результаты применения Д/б -анализа к различным рынкам капитала. Во всех случаях мы найдем фрактальные структуры и непериодические циклы — убедительное доказательство того, что рынки капитала являются нелинейными системами и что гипотеза эффективного рынка вследствие этого под большим вопросом. Представленный в этой главе анализ следует в развитие работ Петерса (1989, 1991). [c.107]
Динамическая система есть нелинейная система с обратной связью. Основные характеристики динамических систем включают в себя чувствительную зависимость от начальных условий, критические уровни и уже знакомые нам из части 2 фрактальные размерности. Важным моментом в понимании нелинейных динамических систем является их зритель-нор ВООТТрИЯТИР ТВ ИССЛЕДОВАНИИ ХЯ РИ УИЛТ-НЫЙ ЯНЯЛ " [c.162]
Численные эксперименты, подобные тому, что мы выполнили с уравнением Хенона, весьма поучительны. Они помогают нам почувствовать движение в нелинейных системах посредством такого эмпирического тестирования. Однако чистому математику это ничего не доказывает. Такого рода математический эксперимент не был бы им даже одобрен. Для чистого математика проблема является решенной только тогда, когда она решена для общего случая. [c.171]
Многие нелинейные системы решены в классическом смысле (подобно тому как было доказано существование числа Фейгенбаумя — гм гтт 10) но МН ГИР други такого ро-шения не имеют. Отображение Хенона остается требую-Щим доказательства . Для практиков, не требующих математического доказательства, численные эксперименты представляют собой подручный способ рассмотрения нелинейных систем, путь интуитивного постижения их, осознания Необходимости преодоления хаоса. Я призываю вас экспериментировать. Лабораторией хаоса становится компьютер. Меняйте параметры и изучайте результаты. Создавайте Св°и собственные аттракторы. Современные компьютеры да- [c.171]
Далее, существует проблема предсказательной частоты. Хаотический аттрактор для американского рынка имеет в среднем четырехгодичный непериодический цикл. Это подразумевает долговременный инвестиционный горизонт. Паккард и др. (Pa kard et al, 1980) показали, что можно предсказать поведение нелинейной системы с помощью линейных методов на коротких интервалах времени. В PanAgora мы прогнозируем с месячной частотой. Это означает, что мы используем месячные данные для предсказания на месяц вперед. В PanAgora мы верим, что надежный путь к созданию богатства — долговременные инвестиции. Среди нашей клиентуры — пенсионные фонды, учреждения, дарственные фонды-Наши клиенты — долговременные институты, освобожденные от уплаты налогов. Накопление богатства посредством биржевой торговли — не единственная их цель. В действительности мы уверены, что устойчивое извлечение прибылей по средством торговой активности является чрезвычайно трУД" ной задачей. [c.254]
Таким образом, задача сводится к распознаванию текущего запаса устойчивости системы по результатам измерения электроэнергетических параметров ее основных узлов нагрузки и адаптированию параметров защит минимального напряжения при изменении нагрузки в процессе эксплуатации системы. Сложность установления соответствия измеряемых электроэнергетических параметров и параметров устойчивости обусловлена явной нелинейностью системы электроснабжения, наличием точек бифуркации в зависимостях, связывающих параметры устойчивости и показатели приборов измерения. Для решения задачи целесообразно использовать методы искусственного интеллекта, обладающие свойством динамического самообучения. В последнее время наиболее эффективно развиваются два метода искусственного интеллекта искусственных нейронных сетей (ИНС) и нечеткой логики [177,173,47,184,100]. [c.143]
Когда создана новая интегрированная нелинейная система, то по законам синергетики она имеет множество путей развития, т. е. путь ее развития не единствен, не определен, как и пути развития элементарных структур, ее составляющих. Путей развития много, но их число не бесконечно. Иными словами, реализуемы в данной нелинейной системе не обязательно те пути развития, которые выбрал субъект управления. В данном случае знание неких ярйдпвдмонных пов запрета весьма ценно при выборе способа управления. Здесь главный управленческий принцип совпадает с врачебным принципом Не навреди [c.327]
Пытаясь объяснить, как системы могут трансформировать себя таким образом, теоретики хаоса особенно заинтересовались гем, что происходит, когда систему выталкивают из состояния равновесия в ситуацию на грань хаоса . Здесь она встречается с точкам к бифуркации , напоминающими развилку на дороге, ведущую к разным свойствам В этих точках энергия системы может организоваться через неподдающиеся прогнозированию скачки в разные системные состояния. Если старый доминирующий апрактор может рассеять энергию и нестабильность, потенциальные перемены исчезнут и система вернется в состояние, похожее на предыдущее. Если же, наоборот, верх одерживают новые влияния, это может привлечь энергию для новой конфигурации. Точки бифуркации и связанные с ними аттракторы всегда существуют как скрытые потенциалы в любой сложной нелинейной системе. Они предупреждают о потенциальной возможности самоорганизации и эволюции новых форм. Тем не менее путь эволюции системы совершенно непредсказуем, потому что благодаря ее сложности и нелинейности самые незначительными изменения могут привести к огромным результатам. [c.289]
В данной работе представлено строгое решение задачи синтеза оптимального по быстродействию управления для одной нелинейной системы. Одним из практических примеров этой системы являегся цроцесс движения водошмещашщего судна при выполнении важнейшего из маневров - поворота судна. [c.144]
