Я-регрессия а (X) = Х в, где в — вектор неизвестных параметров, и для всех X Я-дисперсия а2 (X) = а2 и а2 также неизвестно, Пусть далее у (в, а) — Еря ( — Х Э, а), где Е — символ математического ожидания по мере dF (у, X) тогда [c.220]
В экономических и технологических исследованиях при фиксированном значении регрессора X часто рассматривается многомерный отклик Y = Чг/ (X)Q + е, где Y — (/X 1) -вектор наблюдений при значении регрессора X, Чг — известная (/ X р)-матричная функция X, в — (рх 1)-вектор неизвестных параметров, а е — (/X 1)-вектор ошибок N (О, V), где V — неизвестная положительно определенная (/ X /)-матрица. Оценка вектора в многомерной регрессии проводится одновременно с оценкой матрицы V путем итеративного решения нелинейной системы уравнений. Разработаны устойчивые методы оценки многомерной регрессии. Многомерная регрессия может использоваться при описании многомерных распределений. [c.250]
Роль и место непараметрических методов. Непараметрический подход к оцениванию позволяет ослабить два основных требования классической постановки регрессионной задачи. Первое — предположение о том, что Е (у Х) как функция X представима в виде / (X В), где /(...,...) — известная функция своих аргументов, а В — вектор неизвестных параметров, оцениваемый по выборочным данным, — заменяется на более слабое предположение, что / (X) — непрерывная и гладкая функциях. Второе — требование постоянства а2 (X) — дисперсии случайной погрешности — заменяется на предположение непрерывности а2 (X). [c.321]
Применим к (14.27) метод наименьших квадратов. В результате для вектора неизвестных коэффициентов б получаем оценку [c.416]
Здесь а - вектор неизвестных параметров размерности (т + 1). Пусть имеется л наблюдений вектора х и зависимой переменной у. Для того, чтобы формально можно было решить задачу, то есть найти некоторый наилучший вектор параметров, должно быть л > т+1. Если это условие не выполняется, то можно найти бесконечно много разных векторов коэффициентов, при которых линейная формула связывает между собой х и у для имеющихся наблюдений абсолютно точно. Если, в частном случае, л = /и+1 (например, при двух объясняющих переменных в уравнении у = а +а +а и трех [c.307]
С формальной точки зрения многие проблемы оптимального управления могут быть сведены к задачам линейного или нелинейного программирования большой размерности, так как каждой точке пространства состояний соответствует свой вектор неизвестных переменных. Все же, как правило, движение в данном направлении без учета специфики соответствующих задач [c.197]
В этой главе классическая регрессионная схема обобщается в двух направлениях. Первое связано с отказом от предположения, что независимые переменные являются неслучайными величинами. Оказывается, что при выполнении некоторых естественных условий МНК-оценка вектора неизвестных параметров сохраняет основные свойства МНК-оценки в стандартной модели. Главным условием, гарантирующим наличие этих свойств, является некоррелированность (независимость) матрицы регрессоров X и вектора ошибок е. [c.148]
В общем случае эта матрица зависит от вектора неизвестных параметров в, поэтому для построения асимптотически оптимальной оценки обычно используют двухшаговые или многошаговые процедуры. Например, на первом этапе находится оценка 0(0) путем решения задачи (13.54) (т.е. с единичной весовой матрицей). Затем строится состоятельная оценка матрицы [c.392]
Правая часть этого выражения является при фиксированных xi i = 1,. . . , п, функцией от вектора неизвестных параметров 9, [c.19]
Как и в простой линейной регрессии, для определения вектора неизвестных параметров а = (а0,. .., a f модели (5.32) по результатам наблюдений используется метод наименьших квадратов (МНК). [c.76]
В заключение отметим, что для применения обобщенного метода наименьших квадратов необходимо знание ковариационной матрицы вектора возмущений Q, что встречается крайне редко в практике эконометрического моделирования. Если же считать все я(л+1)/2 элементов симметричной ковариационной матрицы Q неизвестными параметрами обобщенной модели (в дополнении к (р+l) параметрам (3/), то общее число параметров значительно превысит число наблюдений я, что сделает оценку этих параметров неразрешимой задачей. Поэтому для практической реализации обобщенного метода наименьших квадратов необходимо вводить дополнительные условия на структуру матрицы Q. Так мы приходим к практически реализуемому (или доступному) обобщенному методу наименьших квадратов, рассматриваемому в 7.11. [c.155]
Пусть, например, у вектора ха неизвестна всего одна k -я координата. Ее значение находится из оставшихся по формуле [c.135]
| Рисунок 6. Восстановление пропущенных значения с помощью главных компонент. Пунктир - возможные значения исходного вектора с k = 1 неизвестными координатами. Наиболее вероятное его значение - на | 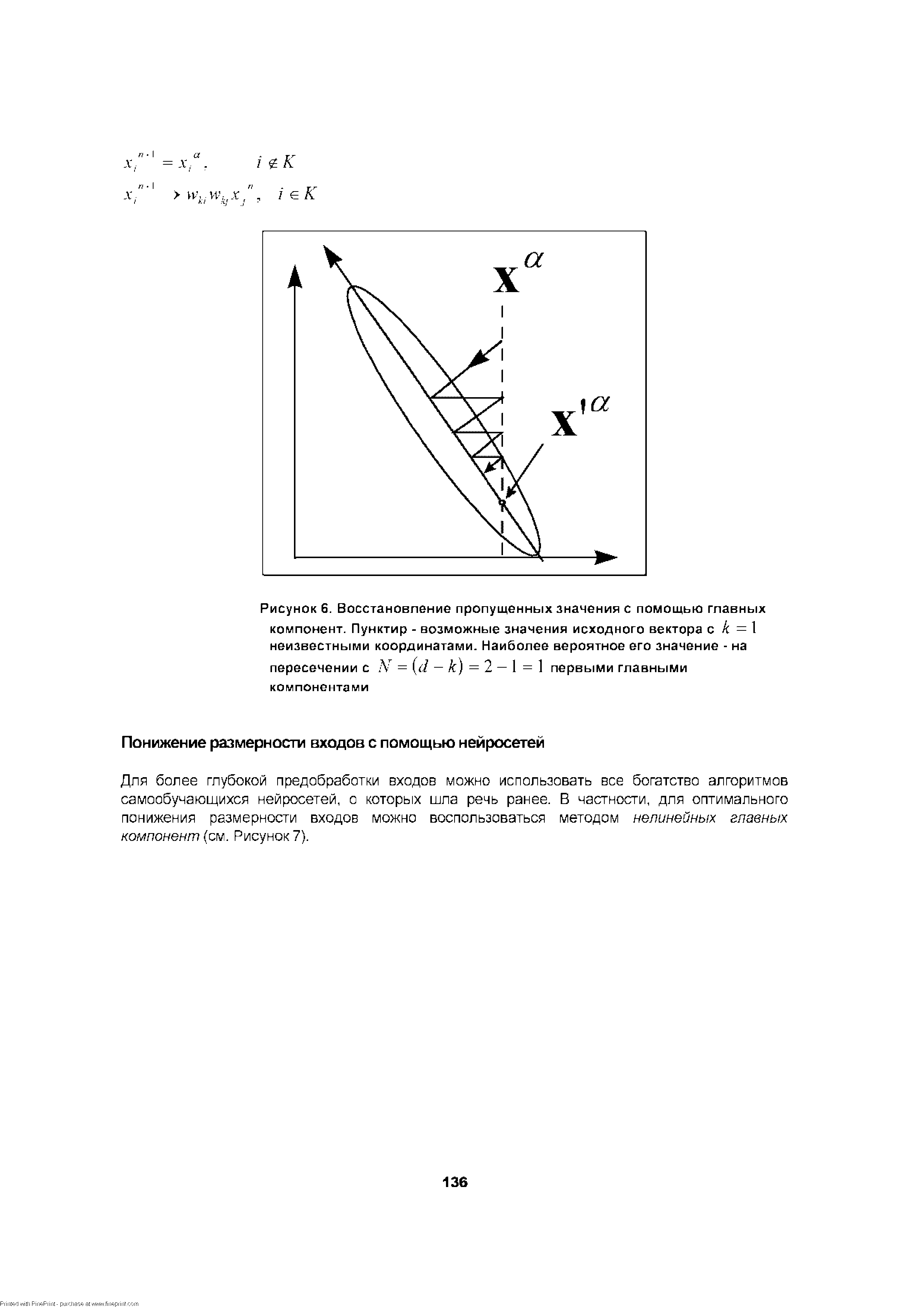 |
Они должны удовлетворять упомянутому выше требованию каждый раз выделенная главная компонента должна воспроизводить максимум дисперсии. На неизвестные векторы коэффициентов aj в (7.29) накладываются дополнительные ограничения [c.316]
Отсюда получаем новую, более точную, чем (2.14), оценку сверху Для неизвестного множества выбираемых векторов [c.67]
Теперь рассмотрим ситуацию, когда /-й критерий важнее у-го, а он, в свою очередь, важнее некоторого к-то критерия, / у, j t к, i к. Здесь также имеются два сообщения об относительной важности критериев, но они не являются взаимно независимыми. Тем не менее, для учета этого набора информации и формирования нового векторного критерия также можно дважды применить теорему 2.5, в которой идет речь об учете информации об относительной важности одного критерия в сравнении с другим. Сначала следует пересчитать к-й критерий для того, чтобы воспользоваться информацией о том, что у-й критерий важнее к-го. Затем необходимо пересчитать у-й критерий для учета информации о том, что /-й критерий важнее у-го. В результате будет образован новый векторный критерий, у которого все компоненты за исключением у-й и к-й остались прежними. Множество парето-оптимальных решений (парето-оптимальных векторов) относительно нового векторного критерия будет представлять собой оценку сверху для неизвестного множества выбираемых решений (выбираемых векторов). [c.95]
Существо полученных здесь результатов можно выразить следующим образом информация об относительной важности критериев полна в том смысле, что только на ее основе для любой задачи определенного достаточно широкого класса можно с любой степенью точности определить неизвестное множество недоминируемых векторов (недоминируемых решений). Если же число возможных векторов конечно, то множество недоминируемых векторов может быть построено точно и полностью. Таким образом, научившись выявлять информацию об относительной важности, можно успешно находить множество недоминируемых решений и векторов, не привлекая информации никакого другого типа. [c.131]
Более точно поставленный выше вопрос можно сформулировать следующим образом возможно ли, используя лишь конечный набор информации об относительной важности критериев, получить сколь угодно тонное представление о неизвестном множестве недоминируемых векторов Оказывается, на этот вопрос в принципе можно ответить положительно. В принципе — так как придется несколько сузить класс рассматриваемых задач многокритериального выбора, уже ограниченных рамками аксиом 1-4. [c.132]
Ниже будет показано, что для определенного класса задач многокритериального выбора нужно лишь научиться успешно извлекать и грамотно использовать информацию об относительной важности критериев. Этого вполне достаточно для того, чтобы, по крайней мере, теоретически получить сколь угодно точное представление о неизвестном множестве недоминируемых векторов (и недоминируемых решений). Такое положение свидетельствует о важной роли информации об относительной важности критериев в процессе принятия решений. [c.132]
Поставленный в предыдущем пункте вопрос о полноте информации об относительной важности критериев теперь в геометрических терминах примет следующую форму насколько близким к неизвестному отношению предпочтения у можно получить отношение >и, используя лишь различного рода конечные непротиворечивые наборы векторов и1, и1,..., ик. Другими словами, имеется ли принципиальная возможность за счет выбора указанного набора векторов сколь угодно точно приблизить отношение >м к неизвестному отношению предпочтения >- [c.133]
Для упрощения последующего решения поставленный вопрос переведем в плоскость конусов отношений и сформулируем его так возможно ли за счет выбора набора векторов и1, и2,. .., ик получить конус М сколь угодно близким к неизвестному конусу К ) При этом число векторов к не фиксировано и может быть любым конечным числом. [c.133]
Теоретическое обоснование описанного метода последовательного сужения множества Парето на основе количественной информации об относительной важности критериев приведено в пятой главе. Доказанная в ней теорема 5.3 утверждает, что во многих случаях, когда множество возможных векторов состоит из конечного числа элементов (это условие заведомо выполняется, если конечным является множество возможных решений), на основе конечного набора информации об относительной важности критериев, можно точно построить неизвестное множество недоминируемых векторов (а значит, и множество недоминируемых решений). К сожалению, этот результат не является конструктивным в том смысле, что в нем не указывается, какой именно набор информации следует при этом использовать. Неизвестно также, какое количество сообщений об относительной важности при этом нужно иметь. Решение этих вопросов в сильной степени зависит от конкретного вида множества возможных решений и участвующих в задаче выбора критериев. Тем не менее, эта теорема имеет важное теоретическое значение, поскольку она обосновывает описанный метод последовательного сужения множества Парето. По сути дела она утверждает, что при решении задач многокритериального выбора следует лишь научиться выявлять информацию об относительной важности критериев и умело ее использовать на основе только такой информации можно полностью и точно построить множество недоминируемых решений для произвольной задачи многокритериального выбора из достаточно широкого класса, в которой множество возможных решений конечно. Если же указанное множество не является конечным, то с помощью одной информации об относительной важности можно получить сколь угодно точное приближение к искомому множеству недоминируемых решений (см. теорему 5.2). Аналогичное утверждение справедливо не только для решений, но и для векторов. [c.159]
Lagrangian] — вспомогательная функция, применяемая при решении задач математического программирования, в частности линейного программирования. Образуется путем прибавления к целевой функции скалярного произведения двух векторов вектора разностей между константами ограничений и функциями ограничений и вектора (неизвестных) множителей, называемых множителями Лагранжа [c.166]
Таким образом, вырожденность матрицы V накладывает некоторые ограничения на вектор неизвестных параметров /3, кроме случая, когда Т X = О, или, что то же самое, ol(X) С ol(V). Если предположить, что ol(X) С ol( V), то модель (у, X (3, <т2 V) с вырожденной матрицей V эквивалентна модели без ограничений (Sfy, Sf X /3, сг2Л), где Л — не вырождена, и, следовательно, применима теорема 4. Эти рассуждения приводят к теореме 8. [c.344]
Общая математическая модель линейной регрессии имеет вид Y = X + е, где Y — (п X 1)-вектор наблюдений, X = (Xi... Хп) — (п X р)-матрица плана экспериментов, Xk — регрессор й-го наблюдения, в — (р X 1) -вектор неизвестных параметров, s — (п X 1) — вектор случайных ошибок. В классической постановке задачи линейной регрессии предполагается, что г N (0, сг21п), где 1П — (п X п)-единичная матрица. Оценки по методу наименьших квадратов (мнк-оценки) отыскиваются из условия минимизации по 0 величины Y — Х0 . Когда Х Х =т О (ранг X равен р), [c.249]
Среди экзогенных переменных xtj могут быть характеристики, зависящие только от индивидуума и не зависящие от альтернативы. Если, например, анализируется проблема выбора профессии, то естественно включить в xtj такие факторы, как возраст, уровень образования, социальный статус и т.п., которые не зависят от профессии. Выделим такие переменные ж - = [yL,zJ], и соответствующим образом разобьем вектор неизвестных параметров на две компоненты /3 = ру ]- Тогда числитель и знаменатель правой части формулы (12.13) будут содержать общий сомножитель exp(z tS), а это означает, что вектор параметров S оценить невозможно (неидентифицируемость). Следовательно, если необходимо учесть индивидуальные эффекты, logit-иоделъ множественного выбора должна быть модифицирована. Например, можно считать, что коэффициенты 8 могут зависеть от альтернативы, т.е. utj = y t i + z t j- В примере с выбором профессии подобное предположение выглядит реалистичным при одном и том же уровне образования полезность разных профессий разная (при прочих равных). [c.332]
Пусть далее точное число Л/ объектов в области поиска заранее неизвестно. Предполагается известной лишь производящая функций- соответствующей случайной величины Ц, (z)= 2Lp(N= )i.. Каждый из объектов поиска характеризуется своим 1 —мерным вектором значений параметров X = (X , .,.Х . Априорная информация о, значениях параметров каждого из объектов задается t —мерной плотностью распределения . / °(л L) X Lez j 7 < R г (I - J, < ,.,. N). Пару V/o (2.) ffaj будем называть априорным состоянием природы. [c.79]
К сожалению, хотя теоретически характеристики нейронной сети с прямой связью стремятся к байесовской, в применении их к практическим задачам выявляется ряд недостатков. Во-первых, заранее неизвестно, какой сложности (т.е. размера) сеть потребуется для достаточно точной реализации отображения. Эта сложность может оказаться чрезмерно большой. Архитектура сети, т.е. число слоев и число элементов в каждом слое, должна быть зафиксирована до начала обучения. Эта архитектура порождает сложные нелинейные разделяющие поверхности в пространстве входов. В сети с одним скрытым слоем векторы образцов сначала преобразуются (нелинейным образом) в новое пространство представлений (пространство скрытого слоя), а затем гиперплоскости, соответствующие выходным узлам, располагаются так, чтобы разделить классы уже в этом новом пространстве. Тем самым, сеть распознает уже другие характерис- [c.46]
После того, как сеть обучена, становится возможным проследить для каждого входного решающего (determinant) вектора результаты классификации реальных доходов. Для каждого временного отрезка мы можем вычислить так называемое решающее значение классификации. Эта величина показывает, насколько оба внутренних выходных сигнала были далеки от порога, установленного для принятия решения ( сила сигнала ). В нашей реализации мы просто берем среднее сил обоих сигналов. Расстояние от сигнала до порога может принимать значения от 0 до 0.5. Мы берем 0.5 за 100%, так что величина решающего значения может меняться от 0 до 100. Теперь можно определить вклад каждой из компонент входного вектора в решающую способность на взятом отрезке времени. Делается это так временно предполагается, что значение компоненты неизвестно, и изучается изменение решающей способности на выходе. Вместо неизвестного входного значения внутрь нейронной сети вводится среднее арифметическое значение (или безусловное математическое ожидание) соответствующих входных значений. После того, как влияние всех входов вычислены, они масштабируются так, чтобы наибольшая абсолютная величина вклада у каждого входа равнялась 100. В табл. 6.7 представлен репрезентативный временной срез выходных значений. [c.148]
Из приведенных доказательств теорем, посвященных учету различного рода информации об относительной важности критериев, можно усмотреть вполне определенную схему, на основе которой получаются соответствующие формулы для пересчета нового критерия. Кратко эту схему можно описать следующим образом. С самого начала, когда еще нет никакой информации об относительной важности критериев, справедливо лишь включение R" с К, где символом А"обозначен острый выпуклый конус (неизвестного) конусного отношения >. Указанное включение выполняется благодаря аксиоме Парето. Наличие в общем случае некоторого набора информации, состоящего из к сообщений об относительной важности критериев, на геометрическом языке означает задание к векторов у1 е Rm, для которых выполнено у > 0т или, что то же самое, у е К, i = 1, 2,..., к. Далее вводится острый выпуклый конус М, порожденный векторами е1, е1,..., ет, у у2,. ..,ук. Этот конус определяет конусное отношение того же самого класса, что и неизвестное отношение предпочтения >, но более широкое, так как М с К. Конус М является конечнопорожденным, а значит многогранным. Число компонент нового векторного критерия в точности совпадает с числом (т - 1)-мерных граней конуса М, а нормальные (направленные [c.122]
