Этот принцип демонстрирует особую, исключительно важную роль множества парето-оптимальных решений в теории принятия решений. [c.37]
Равенство P(Y) = f(Pf(X)) естественным образом связывает множество парето-оптимальных решений и парето-оптимальных векторов. В соответствии с ним, зная множество парето-оптимальных решений, можно найти соответствующее множество парето-оптимальных векторов. Справедливо и, в определенном смысле обратное, утверждение. А именно, располагая множеством парето-оптимальных векторов Р(Y) по формуле Pf(X) = f l(P (У)), где в правой части равенства записан прообраз множества Р У), можно пытаться строить соответствующее множество парето-оптимальных решений. Таким образом, в идейном отношении эти два множества полностью определяют друг друга, хотя попытка построение одного из них на основе второго может натолкнуться на определенные вычислительные трудности (в большей степени это относится к построению множества парето-оптимальных решений). [c.38]
Теперь рассмотрим ситуацию, когда /-й критерий важнее у-го, а он, в свою очередь, важнее некоторого к-то критерия, / у, j t к, i к. Здесь также имеются два сообщения об относительной важности критериев, но они не являются взаимно независимыми. Тем не менее, для учета этого набора информации и формирования нового векторного критерия также можно дважды применить теорему 2.5, в которой идет речь об учете информации об относительной важности одного критерия в сравнении с другим. Сначала следует пересчитать к-й критерий для того, чтобы воспользоваться информацией о том, что у-й критерий важнее к-го. Затем необходимо пересчитать у-й критерий для учета информации о том, что /-й критерий важнее у-го. В результате будет образован новый векторный критерий, у которого все компоненты за исключением у-й и к-й остались прежними. Множество парето-оптимальных решений (парето-оптимальных векторов) относительно нового векторного критерия будет представлять собой оценку сверху для неизвестного множества выбираемых решений (выбираемых векторов). [c.95]
Специфичность проекта и состава инвесторов определяет сб-держание, структуру и способы формирования показателей эффективности для конкретного проекта. Необходимо осуществлять выбор компромиссного решения на основе согласования интересов всех участников проекта это решение должно принадлежать множеству Парето-оптимальных решений. [c.218]
На множестве возможных выигрышей выделяется множество Парето-оптимальных решении, т.е. множество точек, принадлежащих S, для которых увеличение выигрыша одного из игроков возможно только за счет уменьшения выигрыша его партнера. Очевидно, множество таких точек образует северо-восточная граница множества S. [c.231]
Применение принципа Эджворта-Парето позволяет из множества всех возможных исключить заведомо неприемлемые решения, т. е. те, которые никогда не могут оказаться выбранными, если выбор осуществляется достаточно разумно . После такого исключения остается множество, которое называют множеством Парето или областью компромиссов. Оно, как правило, является достаточно широким, и в процессе принятия решений неизбежно встает вопрос о том, какое именно возможное решение выбрать среди парето-оптимальных Выражаясь иначе, какие из парето-оптимальных решений следует удалить для того, чтобы произвести дальнейшее сужение области компромиссов и, тем самым, получить более точное представление об искомом множестве выбираемых решений Этот вопрос при решении практических многокритериальных задач является наиболее трудным и наименее проработанным к настоящему времени. [c.10]
Множество парето-оптимальных векторов. Вектор/(х ) при парето-оптимальном решении х называют парето-оптимальным вектором (парето-оптимальной оценкой) решения х или просто парето-оптимальным вектором, а множество всех таких векторов — множеством парето-оптимальных векторов (парето-оптимальных оценок). Для этого множества используют обозначение P(Y). Таким образом, [c.37]
Теорема 1.3. В случае конечного множества возможных векторов У (в частности, если конечно множество возможных решений X) существует хотя бы одно парето-оптимальное решение и, соответственно, хотя бы один парето-оптимальный вектор, т. е. Pf(X) 0, Р ) 0. [c.39]
Теорема 4.4 (в терминах векторов). Предположим, что выполнены аксиомы 1-4 и имеется набор из двух сообщений о том, что i-u критерий важнее k-го с коэффициентом относительной важности Qik, а также что j-u критерий важнее k-го с коэффициентом относительной важности Qjk. Тогда для любого непустого множества выбираемых векторов Sel Y справедливы включения (4.1), где Р ) — множество парето-оптимальных векторов в задаче с множеством возможных решений X и векторным критерием g вида [c.106]
Теперь обсудим, каким образом МДЦ можно использовать при наличии дополнительной информации об относительной важности критериев в случае, когда множество возможных решений состоит из бесконечного числа элементов (например, задано в виде множества решений некоторой системы линейных неравенств). Для иллюстрации сначала рассмотрим самую простую ситуацию, — когда имеется всего три критерия и первый критерий важнее второго с некоторым коэффициентом относительной важности. Будем считать, что другой информации нет, причем получающееся в результате учета этой информации множество парето-оптимальных векторов бесконечно. Спрашивается, каким образом произвести дальнейшее сужение области поиска или же более того — остановить выбор на каком-то одном из возможных векторов С этой целью можно по известной формуле 612/1 + (1 - 0i2)/> пересчитать менее важный второй критерий и, тем самым, образовать новый векторный критерий, в котором первый и третий остались прежними. Именно второй, измененный критерий следует взять в качестве некоординатного и задать определенный ряд его значений для получения соответствующих двумерных сечений. Сравнивая представленные на дисплее сечения, можно получить наглядное представление о структуре множества Парето, соответствующем новому векторному критерию, и попытаться выбрать из этого множества какой-то один определенный (компромиссный) вектор у, у, у )- Этот [c.168]
Заметим, что все элементы, принадлежащие полученному по алгоритму компромиссному множеству, - Парето-оптимальны. Конечно, это упрощенный алгоритм поиска совпадающих решений участ- [c.42]
Множество всех Парето-оптимальных решений образуют рубеж Парето или, что тоже рубеж эффективности. Эти два термина используются в литературе как синонимы. [c.247]
Из определения Парето-оптимальности следует простой переборный алгоритм нахождения множества Парето-оптимальных элементов. Поскольку Парето-оптимальность определяется не абсолютными, а относительными значениями оценок объектов (вариантов решений) по значениям их параметров, то для реализации алгоритма достаточно иметь информацию о типе отношений между каждой парой объектов, т.е. знать существует ли между ними отношение строгого предпочтения или нет. Поэтому введем булеву переменную [c.249]
Множество Парето-оптимальных распределений может быть наглядно представлено с помощью ящика Эджворта. В случае 2-х игроков Парето-оптимальное решение может быть найдено с помощью фиксации уровня полезности одного из игроков (скажем. Игрока 2) и поиска максимума функции полезности другого игрока. [c.235]
Решением проблемы взаимодействий между центром и АЭ является множество Парето-оптимальных сочетаний экономических показателей элементов системы, при которых критерии оптимальности каждого АЭ и центра нельзя улучшить, не ухудшив значений критериев оптимальности других субъектов взаимодействия. В ряде случаев возможно сужение множества Парето с выделением ядра - множества таких вариантов сочетаний [c.188]
В рамках рассматриваемой модели многокритериального выбора принцип Эджворта-Парето может быть сформулирован в виде утверждения о том, что множество выбираемых решений содержится в множестве Парето. Иначе говоря, каждое выбираемое решение является парето-оптимальным. Математический эквивалент этому высказыванию — включение одного множества в другое. Для того чтобы доказать это включение, следует определенным образом ограничить весь класс задач многокритериального выбора, наложив специальные требования на указанные выше три объекта. Эти требования (аксиомы) относятся главным образом к отношению предпочтения ЛПР и могут быть интерпретированы как рациональное (или разумное , последовательное ) поведение в процессе выбора. Кроме того, среди этих требований имеется условие согласованности отношения предпочтения ЛПР и векторного критерия, поскольку каждый из этих двух объектов выражает определенные устремления (цели) одного и того же ЛПР, и потому они обязаны быть каким-то образом связаны друг с другом. [c.10]
Сужение множества Парето на основе информации о том, что одна группа критериев важнее другой группы. На основе следующей теоремы в процессе принятия решений из множества всех парето-оптимальных векторов можно удалять те, которые заведомо не могут оказаться выбранными. [c.83]
Определение множества эффективных решений составляет важный этап в последовательной процедуре выбора решений и основывается на использовании принципа Парето (сильная зависимость всех членов группового ЛПР выражается в общности целей всех членов группы). Его можно применять для всех классов группового и многокритериального выбора для нахождения эффективных решений. Как правило, применение этого принципа дает возможность определить не одно, а некоторое подмножество эффективных решений. Поэтому понятие оптимального решения не обязательно означает единственное решение. Это в общем случае подмножество решений. В тех случаях, когда эффективное решение является единственным, то оно является окончательным оптимальным решением. [c.574]
Очевидно, что точка (х, . .. хп), доставляющая максимум полезности U (е, а), принадлежит множеству таких допустимых точек задачи (6.7.7) — (6.7.9), которые не могут быть улучшены сразу по двум критериям — ем а. В теории многокритериальной оптимизации такие решения называются Парето-оптимальными, или эффективными. [c.427]
| Рис. 6.18. Восходящая дуга АВ соответствует Парето-оптимальному множеству решений | 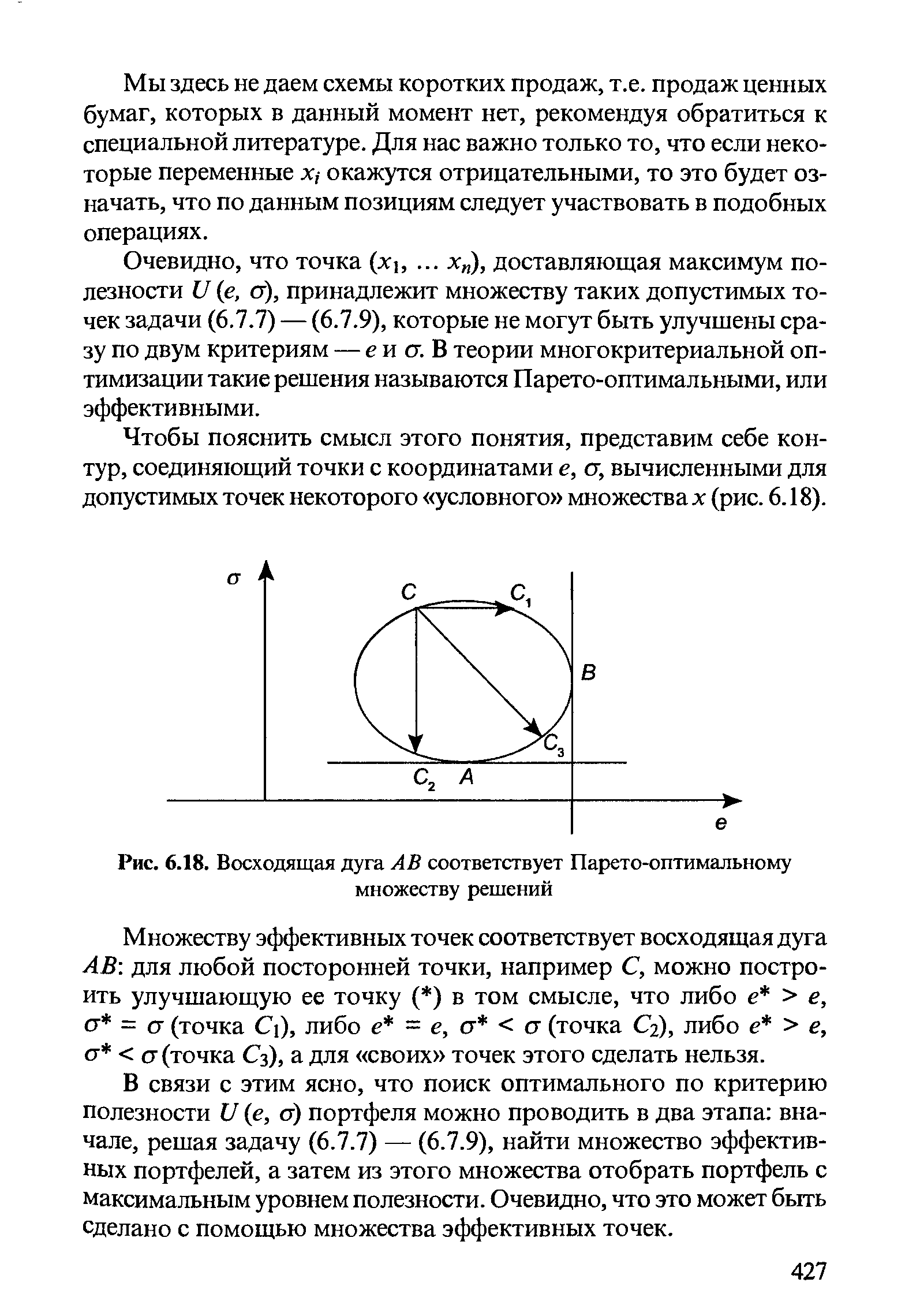 |
Дайте определение Парето-оптимального множества, переговорного множества и решения Нэша для кооперативных игр. [c.244]
Если функция общественного благосостояния является функцией индивидуальных полезностей потребителей, производственные множества являются конусами, то в условиях заданной системы налогообложения общественный выпуск лежит на границе Парето. Иначе говоря, если z - чистый общественный выпуск (производство в общественном секторе за вычетом государственного потребления), у - частный выпуск, то решение задачи максимизации благосостояния принадлежит границе множества Z+Y 28. Таким образом, в условиях эффективно функционирующего государственного сектора экономики система косвенных налогов может приводить к общественно-оптимальному решению. [c.102]
Предложены методы решения задачи выбора вектора управления поликорпоративной системой среди управляющих воздействий, во-первых, с использованием аппроксимации множества Парето, во-вторых, путем последовательного сопоставления оптимальных значений критериев на графе Парето-оптимальных управлений, разработаны алгоритмы формирования управления. [c.114]
Предложен метод выбора вектора управления поликорпоративной системой с использованием аппроксимации множества Парето. Разработанный метод многокритериального выбора по сравнению с непосредственным применением принципа максимина позволяет избежать дифференцирования функции максимума (минимума) для выбора компромиссно-оптимального управления это преимущество особенно важно с учетом того, что функция максимума (минимума) непрерывно дифференцируема не на всей области определения. Применение данного метода в виде формирования минимизирующей последовательности управлений сводит решение многокритериальной задачи управления к последовательности решения скалярных задач оптимизации, для которых разработаны надежные численные методы решения. Использование предложенного метода наряду с получением конечного практически значимого результата - выбора минимаксно-оптимального управления - позволяет получить обширную информацию о структуре множества Парето ценность этой информации заключается в том, что сопоставление минимаксно-оптимального управления с другими элементами множества Парето является инструментом оценки качества этого [c.146]
А Пусть, напротив, для некоторого недоминируемого решения х е Ndom X выполнено соотношение х g P/(X). Тогда, по определению множества парето-оптимальных решений, существует такое возможное решение х е X, что/(х ) > f(x). На основании леммы 1.3 в условиях доказываемого утверждения справедлива аксиома Парето. Поэтому полученное неравенство, в силу аксиомы Парето, влечет соотношение х ух х, которое не совместимо с начальным предположением х е Ndom J. У [c.36]
Рассматриваются вопросы, связанные с выбором решений при наличии нескольких критериев. Впервые в мировой научной литературе строго формулируется известный принцип Эджворта-Парето и устанавливается, при выполнении каких требований применение этого принципа оправдано. Развивается оригинальный общий подход к решению многокритериальных задч при наличии количественной информации об относительной важности критериев. Показывается, что с помощью предлагаемого подхода, используя лишь конечный набор информации об относительной важности критериев, можно достаточно хорошо аппроксимировать множество потенциально-оптимальных решений многокритериальной задачи. [c.2]
Последнее неравенство можно переписать в виде / (х) -/(х ) е Л или f(x) >/( ). Следовательно, соотношение у - у Мдля векторов у = /(х), / = f(x ) равносильно неравенству / (х) >f(x ). Отсюда следует, что множество Р(У), участвующее в (2.11), совпадает с множеством парето-оптимальных векторов многокритериальной задачи, в которой множество возможных решений есть X, а векторный критерий — f вида (2.6). [c.64]
Решением проблемы межрегиональных взаимодействий является множество Парето-оптимальных управлений [58], то есть вариантов сочетаний индикаторов региональных экономик, при которых критерии оптимальности каждого региона нельзя улучшить, не ухудшив значений критериев оптимальности других субъектов взаимодействия. В ряде случаев возможно сужение множества Парето с выделением подмножества - ядра полирегиональной системы, то есть множества таких вариантов сочетаний региональных экономических индикаторов, в реализации которых заинтересованы все регионы однако в системе с противоречивыми интересами выделение ядра невозможно. Единственность решения задачи межрегиональной координации, то есть определение равновесной программы управления, можно обеспечить через конкретизацию стратегий регионов, например, путём максимизации гарантированного результата [135]. [c.260]
Вектор значений показателей / s s Gf называют эффективным (а также неулучшаемым, недоминируемым пли оптимальным по Парето), если не най-, дется другой такой точки множества G/, которая была бы не хуже / по всем показателям и превосходила его хотя бы по одному. На рис. 1.9 изображена одна из эффективных точек. В отличие от нее, точка I/ ,/а] не является эффективной, поскольку точка (/i,/al является более предпочтительной. Множество всех эффективных точек, которое принято называть эффективным множеством (а также недоминируемым множеством или множеством Парето), на рис. 1.9 выделено двойной линией. Те допустимые решения z, для которых /(z) принадлежит эффективному множеству, также принято называть эффективными. При анализе задачи многокритериальной оптимизации заранее можно утверждать лишь, что решение должно быть эффективным, но какое из эффективных решений должно быть выбрано — остается неясным. Для решения эт ого вопроса разрабатываются методы многокритериальной оптимизации, большинство из которых основывается на привлечении к исследованию человека или группы лиц, ответственных за принятие решения. Методы включения человека в исследования можно условно разбить на две большие группы. [c.60]
Располагая определением относительной важности критериев и изучив простейшие его свойства, можно приступить к решению главного вопроса, ради которого это понятие вводилось каким образом учитывать информацию об относительной важности критериев в форме сообщения о том, что один критерий важнее другого Оказывается (это демонстрируется во второй главе книги), если несколько ограничить класс задач многокритериального выбора, для которых справедлив принцип Эджвор-та-Парето, добавлением еще одного достаточно разумного требования (аксиомы) к отношению предпочтения ЛПР, то учет этой информации можно производить очень просто — нужно лишь в соответствии с выведенной несложной формулой пересчитать менее важный критерий, оставив все остальные критерии и множество возможных решений прежними. В результате получится новая многокритериальная задача, множество Парето которой будет уже множества Парето исходной задачи, причем ни одно выбираемое решение исходной задачи не окажется за пределами нового множества Парето. Иначе говоря, при переходе от старого множества Парето к новому произойдет сужение области компромиссов и при этом не будет потеряно ни одно выбираемое (потенциально-оптимальное) решение. Область поиска выбираемых решений после указанного учета информации об относительной важности критериев станет более узкой и, тем самым, задача выбора упростится. [c.12]
Алгоритм нахождения множества Парето. Благодаря наличию указанной выше прямой связи между множествами недоминируемых и парето-оптимальных векторов все результаты, полученные ранее для первого множества, нетрудно переформулировать в терминах второго множества. В частности, для построения множества Pf X) (и Р(У)) в случае конечного множества возможных векторов Yможно применять сформулированный в предыдущем разделе алгоритм нахождения множества недоминируемых решений, заменив в нем сравнение по отношению пред-Почтения >х сравнением по отношению >, которое является иррефлексивным и транзитивным. [c.39]
Утверадение 1.6. Парето-Нэш-область компромиссов содержит практически все УКУ-оптимальные решения, а при выравнивании ресурсов коалиций число решений возрастает и их множество существенно пересекается с ПНОК. Причем на большом числе вариантов большая часть Паре-то-границы ПНОК содержит УКУ-решения. [c.89]
В итоге переговорное множество, образуемое точкой угрозы Г, представлено линией ОЕна Парето-оптимальном множестве решений ДС(рис. 13.3). На линии ДЕМуж и Жена могут договариваться, как часто они будут бывать вместе на одном из зрелищ но при этом, во избежание взаимных угроз, ни одному из развлечений они не должны уделять более своих свободных вечеров. [c.233]
Как и в рассматриваемых ранее моделях, каждое Парето-оптимальное состояние экономики с общественными благами может быть охарактеризовано как решение т задач оптимизации. На их основе можно получить дифференциальную характеристику множества Па-рето-оптимальных состояний экономики с общественными благами в случае, когда функции полезности и производственные функции дифференцируемы. [c.399]
Особенности применения метода аппроксимации. Решение многокритериальной задачи на основе метода аппроксимации множества Парето сводится к последовательности скалярных оптимизационных задач и предусматривает а) формирование К Парето-оптимальных управлений б) построение в соответствии со значениями критериев при этих управлениях гиперболических поверхностей (кривые Pi,ri 1 на рис. 3.1), [c.127]
