Можно показать, что переговорное множество этой игры [c.225]
| Рисунок 13.2. Множество возможных выигрышей, Парето-оптималь-ное множество, точка угрозы, переговорное множество и решение Нэша в кооперативной игре 2-х лиц |  |
Наконец, на переговорном множестве выделяется точка решения Нэша N, в которой достигается максимум произведения превыше- [c.231]
| Рисунок 13.7. Линии угрозы, переговорное множество и решение Нэша для ящика Эджворта | 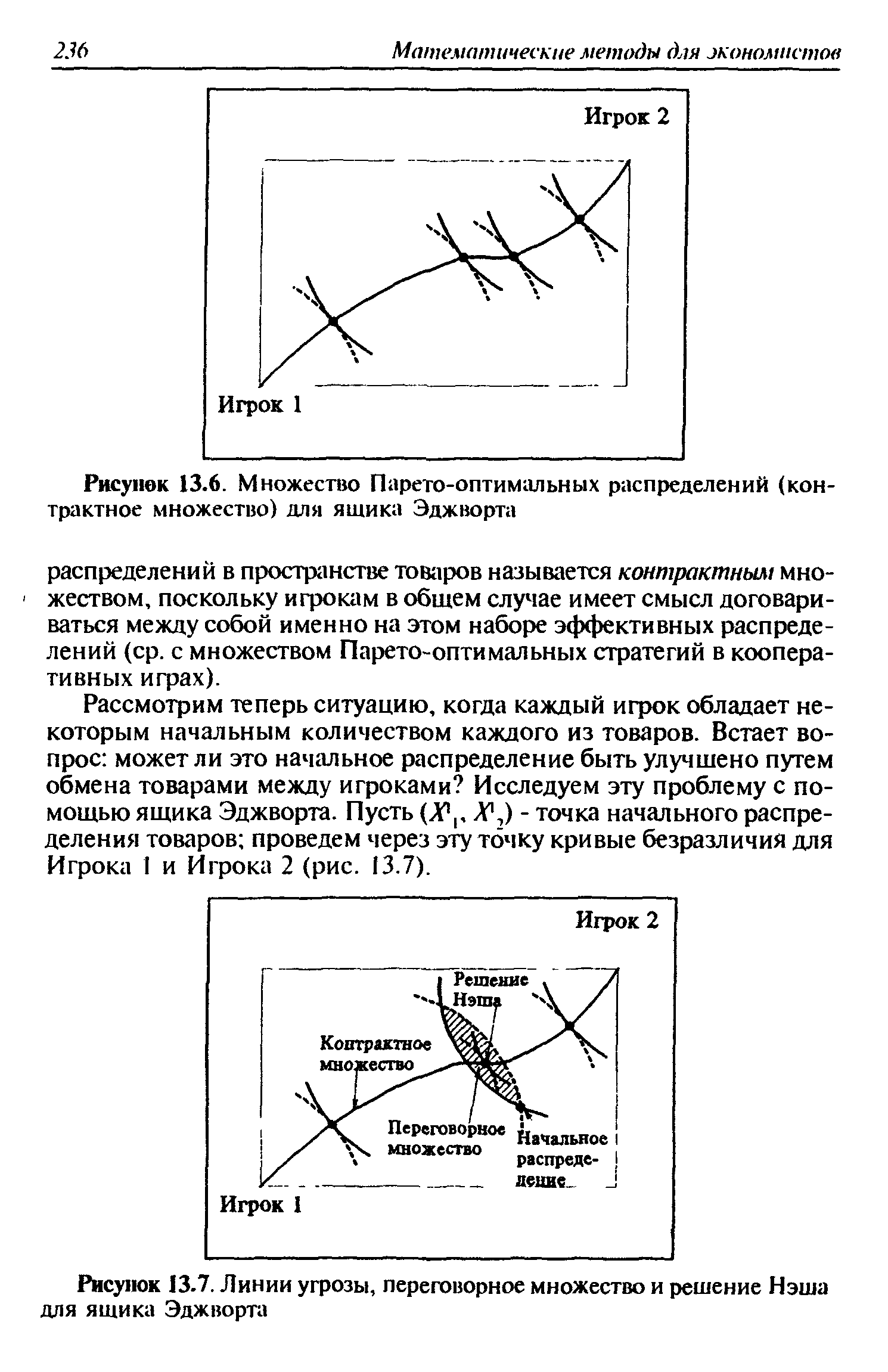 |
Дайте определение Парето-оптимального множества, переговорного множества и решения Нэша для кооперативных игр. [c.244]
Еще сложнее проблемы, возникающие при игре п лиц. Дело в том, что при п > 2 возможно создание коалиций, более могущественных, чем любой из игроков в отдельности. Для этих игр естественным образом обобщается понятие точки равновесия. Доказано, что всякая конечная игра п лиц имеет по меньшей мере одну точку равновесия в смешанных стратегиях. К сожалению, в этих играх нет ни взаимозаменяемости, ни эквивалентности уравновешенных стратегий, и, кроме того, оптимальное множество Парето и переговорное множество определяются гораздо более сложным образом. [c.134]
Говоря неформально, соглашение — любая точка множества 71 Торг — механизм достижения соглашения. Торг эффективен, если соответствующее соглашение принадлежит переговорному множеству. Таким образом, любой эффективный торг ставит в соответствие точке угрозы некоторую точку переговорного множества. [c.387]
Заметим, что, не зная механизма торга, мы не можем предсказать его точный исход (конкретную точку переговорного множества) как уже говорилось, перераспределение прибыли (П Гу будет зависеть от организации переговоров, переговорной силы участников и т.д. Однако можно ожидать, что ничто не будет мешать рациональным хозяйствующим субъектам достигнуть оптимального состояния при этом объем производства экстерналий (но не величина компенсации) не будет зависеть ни от первоначального распределения прав собственности, ни от характера организации переговоров, он будет определяться максимумом суммарной прибыли предприятий. [c.388]
Как правило, таких точек может быть много (см. отрезок АВ на Рис. 119). Назовем соответствующее множество переговорным множеством. Какая именно точка будет выбрана, зависит от процедуры переговоров и переговорной силы участников. Процедуру переговоров (торг) можно представлять как некоторую некооперативную игру, но эта игра остается за рамками модели. [c.550]
Заметим также, что поскольку, вообще говоря, равновесий Курно может быть несколько, то переговорное множество зависит от того, какое из равновесий Курно участники считают за исходную точку (точку угрозы). [c.550]
Как правило, сговор состоит в том, что участники договариваются о квотах выпуска для того, чтобы уменьшить суммарный выпуск и поднять рыночную цену. На Рис. 119 видно, что суммарный выпуск во всех точках переговорного множества ниже, чем в равновесии Курно если через точку равновесия Курно провести прямую yl + у2 = у + уз, то переговорное множество будет лежать ниже этой прямой. Следующее утверждение формализует эту идею. [c.551]
Это будет Парето-оптимум с точки зрения целевых функций Пии, (элемент переговорного множества, наиболее предпочитаемый нанимателем наниматель получит весь излишек от сделки), см. Рис . [c.575]
На основе понятий угрозы и контругрозы дается определение переговорного множества пусть х — дележ в игре v. [c.192]
Переговорное множество всегда непусто и содержит с -ядро. [c.192]
К -ядро и пред- k -ядро всегда непусты. Для любой игры v имеет место равенство K(v) П (v) = K (v) П (v). Кроме того А -ядро лежит в переговорном множестве. [c.195]
Принципиальный подход к ведению переговоров является частью переговорной концепции. Выбор подхода зависит от множества фактов и обстоятельств. [c.582]
Предложение 6.1.3. Переговорное множество всегда непу- [c.220]
АРБИТРАЖНАЯ СХЕМА [ arbitration s heme] — в теории кооперативных игр система разрешения спорных вопросов между участниками коалиции, т. е. обоснование выбора точки решения внутри переговорного множества. [c.24]
ПЕРЕГОВОРНОЕ МНОЖЕСТВО [bargaining set] в анализе некооперативных игр — совокупность точек Парето-оптималь-ного множества, находящихся одновременно правее прямой х1 Р и выше прямой У F на рис. 0.7 к ст. "Оптимальность по Парето". В этих точках увеличение выигрыша одного из игроков возможно только за счет уменьшения выигрыша другого, т.е. они оптимальны по Парето. Название исходит из того, что именно между этими точками партнеры могут делать выбор, договариваясь о взаимно выгодных решениях. Одной из них может быть, напр., точка равновесия по Нэшу. См. также Эджуор-та диаграмма. [c.261]
Первичные ресурсы 260, 384 Первичный профицит бюджета 294 Первичный учет 317 Первичный фактор производства 374 Первообразная функции 125 Первый ортант 153 Переговорное множество 260 Передаточная функция системы 241 Передача информации 261 Перекрестные данные 261 Перекрестный коэффициент эластичности [c.481]
В итоге переговорное множество, образуемое точкой угрозы Г, представлено линией ОЕна Парето-оптимальном множестве решений ДС(рис. 13.3). На линии ДЕМуж и Жена могут договариваться, как часто они будут бывать вместе на одном из зрелищ но при этом, во избежание взаимных угроз, ни одному из развлечений они не должны уделять более своих свободных вечеров. [c.233]
Предполагается, что если участники торга не придут к соглашению, то они окажутся в ситуации, когда их прибыли равны (П15П2). Эта ситуация называется точкой угрозы. Точки (П15 П2) множества Р, для которых выполняется соотношение П1 > Пь П2 > П2 составляют так называемое переговорное множество. В предложенной выше модели переговоров в качестве точки угрозы выбиралась ситуация, которую следует ожидать в отсутствие соглашения. На Рис. 85 отрезок А1В1 представляет переговорное множество для торга с точкой угрозы ST , а А2В2 — переговорное множество для торга с точкой угрозы S2. [c.387]
Действительно, предположим, что ж-дележ и (y,S) — это угроза i против j относительно х. Тогда S = г,Д , где h — оставшийся игрок и yh < 1 — жг- (т.к. уг- > Xi и y(S) = v(S) = 1). Для того, чтобы у j нашлась контругроза на (y,S) мы должны иметь у/,, + Xj < 1. Следовательно, для того, чтобы х принадлежал переговорному множеству необходимо, чтобы для всех игроков i,j,h было выполнего неравенство у/,, < 1 — Xj как только у/,, < 1 — жг-, а это означает, что 1 — жг- < 1 — Xj или Xi > Xj для любых г и j так что х = ( , , ). [c.196]
Сегодня ни для кого не секрет, что достаточно открыть любую газету или журнал, чтобы без труда обнаружить множество объявлений "финансовых прачечных". Они без всяких проблем "обналичат", уводя от налогообложения доходы, облегчая переговорные процессы с любой компанией, увеличивая ваш потребительский потенциал. Не давая оценки деятельности правоохранительных органов, лишь заметим очевидная система мер в оперативном режиме времени в пределах крупных мегаполисов, как сосредоточения "финансовых прачечных", позволит, если не уничтожить полностью, то существенно усложнить процессы прямого "увода" финансовых ресурсов преступниками. Заметим также, что пристального внимания требуют банки, обслуживающие "финансовые прачечные", как правило зарегистрированные на фиктивных лиц. В большинстве случаев механизм "обналички" - результат альянса преступных элементов и банковских служащих, что несомненно нелегко доказать. Уничтожить это явление с использованием современных оперативно-розыскных методов невозможно до тех пор, пока такие альянсы не станут невыгодными для банковских учреждений, т.е. до того момента, когда ответственность за правонарушения будет существенно превышать выгоды, а основные возможности заработка переместятся в сферу легитимной экономики. [c.127]
Предлож ение 6.1.2 Переговорным множеством4 называется множество дележей х таких, что для любой угроды (у, S) игрока i против любого другого игрока j относительно х существует контругроза игрока j относительно (у, S). [c.192]
