Качество средства измерений, отражающее близость к нулю его случайных погрешностей. [c.376]
В первом варианте экономические потери — это среднеотраслевые (среднерайонные или замыкающие) затраты на подготовку (разведку) такого количества запасов, которое покроет (компенсирует) вероятный недобор от случайной погрешности их оценки на стадии разведки. [c.81]
При этом предварительно из вариационного ряда исключают признаки, содержащие систематические ошибки и промахи. Для этого определяют предельную случайную погрешность по формуле С. В. Башинского , 1 [c.57]
Ввиду того, что межремонтный период работы турбобура при одинаковом долоте и методе бурения изменяется в весьма широких пределах вследствие влияния случайных причин, результаты промысловых данных были отработаны методами математической статистики, описанной в предыдущем параграфе. Для этого составляли вариационный ряд значений межремонтного периода работы турбобура в зависимости от вида бурения и диаметра скважины. После предварительного исключения из вариационного ряда грубых промахов для каждого варианта определяли среднее взвешенное значение признака, среднеквадратическое отклонение и предельную случайную погрешность, коэффициент вариации и степень точно сти при вероятности 0,80 и данном числе степеней свободы. [c.60]
При выборе образцового СИ следует учитывать, что в зависимости от значений случайных и систематических погрешностей отношение погрешностей образцового СИ к рабочему должно быть в диапазоне от 1 10 до 1 3. Меньшее отношение, например 1 2, можно применять только при условии, что случайные погрешности малы и погрешность поверяемого СИ определяется в основном систематическими погрешностями, которые можно учесть. [c.11]
Разброс значений выходных сигналов 1т и погрешность определения среднего / зависят от величины случайной погрешности аналитического прибора и однородности СО. Характеристикой этой погрешности может служить среднее квадратическое отклонение сг , [c.45]
Это объясняет некоторые наблюдаемые колебания значений бета. Предположим, в действительности истинный коэффициент бета компании стабилен. Ее явная (оценочная) бета будет колебаться от периода к периоду из-за случайных погрешностей в вычислении. Таким образом, возможно, истинная величина бета более стабильна, чем подразумевают результаты, полученные Шарпом и Купером. [c.200]
Конечно, инвесторы не могут совершенно точно предсказать фактический темп инфляции — случайные погрешности в прогнозах неизбежны. Но мы надеемся, что в среднем на эффективном рынке прогнозы верны. Поэтому среднее отклонение прогнозных оценок должно быть равно нулю. [c.615]
Систематические и случайные погрешности вызываются различными причинами информационными — недостаточной или излишней информацией, личными — строем нервной деятельности и т. д. [c.55]
Случайная погрешность — величина более опасная , чем систематическая, так как причины появления систематической погрешности могут быть выявлены и, следовательно, сама погрешность устранена. Что касается случайной погрешности, то желательно выбирать экспертов, у которых она имеет минимальное значение. Один из возможных путей — определение воспроизводимости оценок данного эксперта во времени. Для этого эксперту предъявляется группа свойств, весомость которых он определяет несколько раз через значительные (один — два месяца) промежутки времени. [c.55]
Однако при исследовании экспертных методов большинство специалистов рассматривает оценки как величины, имеющие только случайные погрешности. Приняв эту посылку, придется признать, что в этом случае отпадает необходимость в группе экспертов, так как с некоторыми допущениями правомочно считать, что оценка весомости какого-то свойства может быть получена в результате усреднения многократных оценок, даваемых только одним экспертом. И если в практике этот способ никогда не применяется, то лишь из-за наличия систематической составляющей, вызванной теми или иными причинами. Когда же обрабатываются оценки группы экспертов, то систематическая составляющая погрешности одного эксперта для данной группы экспертов, рассматриваемой в целом, будет случайной. [c.55]
Предположив, что коэффициент наклона положителен, из уравнения (8.3) можно заметить следующее чем выше доходность на рыночный индекс, тем выше будет доходность ценной бумаги (заметим, что среднее значение случайной погрешности равняется нулю). [c.207]
Случайную погрешность можно рассматривать как случайную переменную, которая имеет распределение вероятностей с нулевым математическим ожиданием и стандартным отклонением, обозначенным ое/6. Таким образом, ее можно рассматривать как результат вращения колеса рулетки специального типа. [c.210]
Например, случайную погрешность ценной бумаги А можно рассматривать как переменную, связанную с колесом рулетки, на котором равномерно расположены целые значения от —10% до +10%7. Это означает, что существует 21 возможный результат вращения колеса рулетки, каждый из которых равновероятен. Отсюда следует, что при заданном наборе чисел среднее значение случайной погрешности равняется нулю [c.210]
Можно заметить, что данное вычисление представляет собой сумму произведений всех возможных результатов на вероятность их появления. Теперь можно показать, что стандартное отклонение данной случайной погрешности равняется 6,06% [c.210]
Рисунок 8.9 представляет колесо рулетки, соответствующее этой случайной погрешности. В общем случае случайные погрешности ценных бумаг соответствуют рулеткам с другими крайними значениями и другими неравномерными интервалами между значениями. Хотя все они имеют математическое ожидание, равное нулю, стандартные отклонения у них могут быть различными. Например, ценная бумага В может иметь случайную погрешность с нулевым ожидаемым значением и стандартным отклонением, равным 4,7б%8. [c.210]
Прямая линия в части (а) рис. 8.10 представляет собой график рыночной модели для ценной бумаги А. Эта линия связана с уравнением (8.4), но без учета случайной погрешности. Соответственно уравнение прямой, построенной для ценной бумаги А, выглядит следующим образом [c.210]
| Рис. 8.9. Случайная погрешность ценной бумаги А | 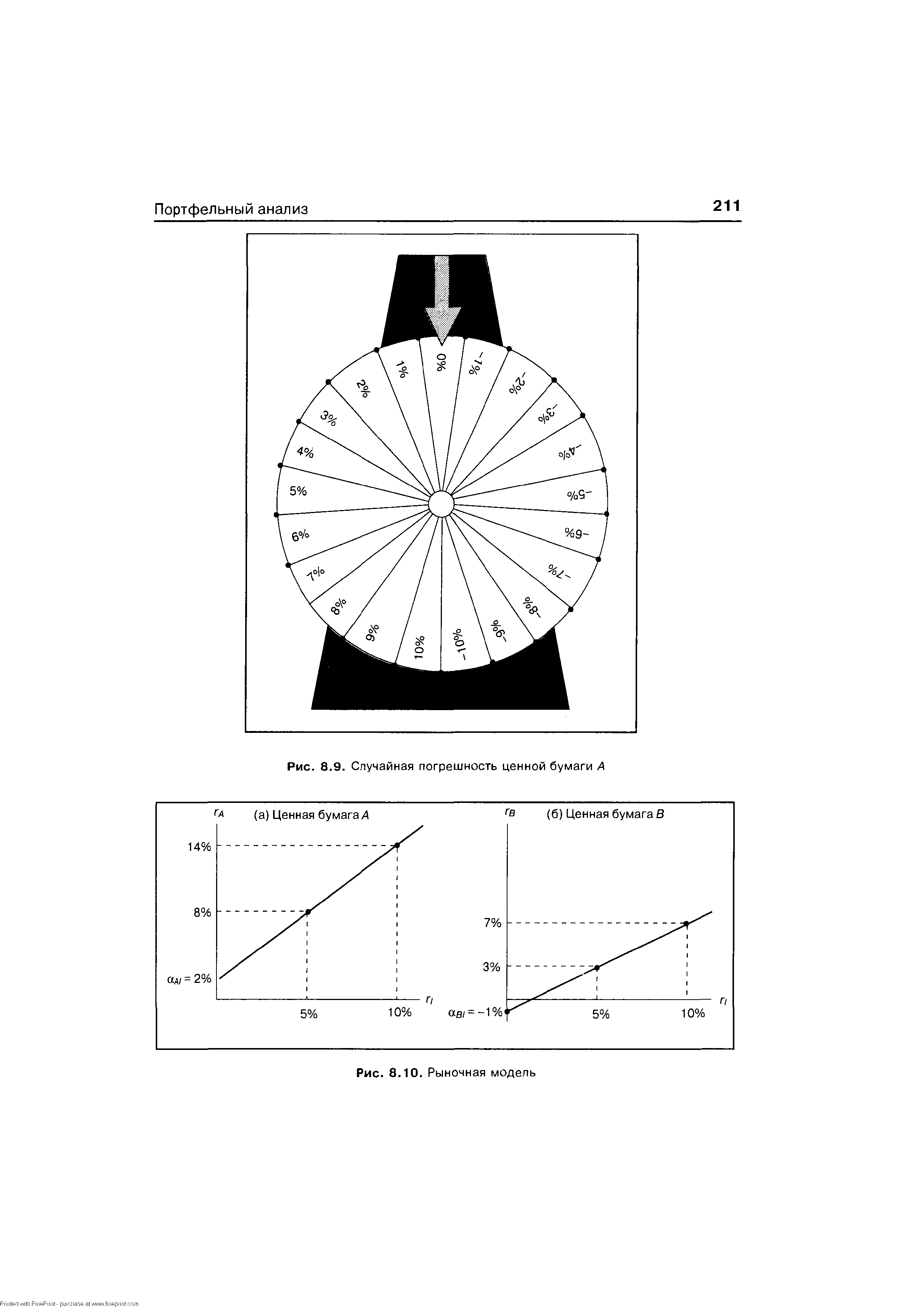 |
В данном случае можно просто сказать, что мы прокрутили колесо рулетки для А и В и в результате этого действия получили значения (которые являются значениями случайной погрешности) — 5% для А и + 4% для В. Можно заметить, что данные значения равняются [c.212]
В уравнениях (8.106) и (8.10в) показано, что координаты точки пересечения с вертикальной осью (ос ) и бета (р ) являются средневзвешенными значениями коэффициентов смещения и беты ценных бумаг соответственно, где в качестве весов берутся их относительные доли в портфеле. Аналогично в уравнении (8. Юг) случайная погрешность портфеля (гр1) является средневзвешенной случайных погрешностей ценных бумаг, где в качестве весов опять берутся их относительные доли в портфеле. Таким образом, рыночная модель портфеля является прямым обобщением рыночных моделей отдельных ценных бумаг, приведенных в уравнении (8.3)". [c.214]
Рассмотрим две ценные бумаги А и Б, о которых шла речь ранее. Эти бумаги имеют коэффициенты бета , равные 1,2 и 0,8 соответственно стандартные отклонения их случайных погрешностей составляют 6,06 и 4,76%. Таким образом, из заданных значений аы = 6,06% и a s = 4,76% следует, что с[= 6, Об2 = 37 и о в= 4,762 = 23. Теперь предположим, что стандартное отклонение рыночного индекса о7 составляет 8%. Это подразумевает, что дисперсия рыночного индекса равняется 82, или 64. Используя уравнение (8.8), получим значения дисперсии для ценных бумаг А и В [c.216]
Рассмотрим, что произойдет при комбинировании первых двух ценных бумаг с третьей ценной бумагой (С) в случае формирования портфеля, состоящего из трех ценных бумаг, взятых в равной пропорции (ХА = Хв= Хс= 0,33). Третья бумага имеет бету , равную 1,0, и случайную погрешность, стандартное отклонение которой (ак) составляет 5,50%. Таким образом, дисперсия случайной погрешности ОЕС равняется 5,52, или 30, а дисперсия ценной бумаги вычисляется по формуле [c.217]
Доходность на индекс рынка не отражает доходности ценной бумаги полностью. Необъясненные элементы включаются в случайную погрешность рыночной модели. [c.218]
Вертикальное смещение, бета -коэффициент и случайная погрешность портфеля являются средневзвешенными значениями смещений, бета -коэффициентов и случайных погрешностей ценных бумаг, входящих в портфель, причем вес каждой бумаги равен ее доле в общей стоимости портфеля. [c.218]
Имеются два портфеля, один инвестирован в компанию по энергоснабжению, другой — в компанию по добыче золота. Каждый портфель имеет коэффициент бета , равный 0,60. Почему для аналитика рынка ценных бумаг интересно знать, что портфель, инвестированный в золотодобычу, имеет большее стандартное отклонение случайной погрешности (собственный риск), чем портфель, инвестированный в энергоснабжение [c.220]
Предполагая, что коэффициент смещения рыночной модели равен 0%, вычислите стандартное отклонение случайной погрешности рыночной модели за данный период. [c.220]
При использовании рыночной модели дисперсия ценной бумаги / может быть оценена как сумма произведения квадрата значения бета -коэффициента ценной бумаги на дисперсию индекса рынка и дисперсию случайной погрешности. Уравнение для данной операции приводилось ранее [c.227]
Дисперсия случайной погрешности (о ) N [c.227]
Будет технически более правильным обозначить стандартное отклонение случайной погрешности как G r так как оно измеряется относительно индекса рынка /. Обозначение /не приводится в данном случае для упрощения записи. [c.228]
Так как диапазон относится к возможным результатам, а интервал — к вероятности возникновения различных результатов, то можно заметить, что колесо рулетки просто является удобной формой представления вероятностного распределения случайной погрешности. Обычно предполагается, что случайная погрешность имеет нормальное распределение. [c.228]
Это возможно в том случае, если ценная бумага В имеет случайную погрешность, которой соответствует колесо рулетки с целыми значениями от —9% до 9%, но с интервалами между каждым целым числом от —5% до 5% в два раза большими, чем интервалы между целыми числами от —9% до —6% и от 6% до 9%. Это означает, что вероятность того, что случайная погрешность примет любое конкретное целое значение между —5% и 5%, равняется 2/з0, в та время как вероятность того, что случайная погрешность примет целое значение из интервала от -9% до -6% и от 6% до 9%, равняется /зо- [c.228]
Если случайная погрешность принимает значение, равное нулю, то это означает, что ценная бумага лежит на линии. Однако вероятность такой ситуации мала для большинства ценных бумаг. [c.228]
Стандартное отклонение случайной погрешности [c.891]
Стандартное отклонение случайной погрешности/ XX2-[(IX)2 / Г] 1/2 = [c.891]
Стандартное отклонение случайной погрешности/ Г-[(SX2/ZX)2] 1/ 2 = [c.891]
Вертикальное расстояние между каждой точкой этой диаграммы и регрессионной линией представляет собой оценку случайной погрешности для соответствующего квартала. Точное расстояние может быть определено, если переписать уравнение (25.16) в следующем виде [c.895]
В таблице 9-3 показаны оценки бета обыкновенных акций 24 крупных компаний коммунального хозяйства и стандартные отклонения этих оценок. Большинство стандартных отклонений в этой группе меньше, чем у компании DE , но они все же достаточно велики для точных оценок бета какой-либо отдельной фирмы (посмотрите на стандартное отклонение для бета enterior Energy). Однако средняя бета 24 компаний в значительной степени надежна. Действительно ли ценные бумаги этих компаний коммунального хозяйства сопряжены с эквивалентным риском Судя по таблице 9-3, это представляется разумным допущением. Основная часть разброса полученных значений бета могла бы быть отнесена на счет случайных погрешностей вычисления. Было бы трудно опро вергнуть гипотезу о том, что "истинное" значение бета одинаково для всех фирм. [c.209]
Выявляемая причина отклонения от заданного качества (Assignable ause) — причина отклонения от заданного качества, например, небрежность рабочего, износ инструмента и т. д., которая может быть выявлена и устранена (в отличие от неизбежных случайных погрешностей), [c.51]
Член уравнения (8.3), известный как случайная погрешность (random error term), просто показывает, что рыночная модель не очень точно объясняет доходности ценных бумаг. Другими словами, когда рыночный индекс возрастает на 10% или уменьшается на 5%, то доходность ценной бумаги А не обязательно равняется 14% или -4% соответственно. Разность между действительным и ожидаемым значениями доходности при известной доходности рыночного индекса приписывается случайной погрешности. Таким образом, если доходность ценной бумаги составила 9% вместо 14%, то разность в 5% является случайной погрешностью (т.е. ei = —5% этот факт будет проиллюстрирован на рис. 8.11). Аналогично, если доходность ценной бумаги оказалась равной -2% вместо —4%, то разность в 2% является случайной погрешностью (т.е. е4 = +2%). [c.209]
Случайная погрешность позволяет сделать предположение, что при данной доходности на рыночный индекс действительная доходность ценной бумаги обычно лежит вне прямой, задаваемой уравнением рыночной модели10. Если действительные доходности на ценные бумаги А и В составляют 9 и 11% соответственно, а действительная доходйость на индекс составляет 10%, то можно заметить, что действительные доходности на А и В состоят из трех следующих компонентов [c.212]
