Гарантирующая стратегия 221 Генерирование случайных чисел 269 Горизонт планирования 43 Граф сетевой 180 [c.301]
Дополнительно вводится граф сетевой структуры В с вершинами Xl,X2,...,Xi,...,Xn . Дуга
Графы 1—3 заполняются на основании сетевого графика. Затем определяются раннее начало и окончание работ. При этом раннее начало работ, не имеющих предшествующих работ, равно [c.105]
Не менее прост и расчет показателей сетевою графика в таблице (табл. 2.1). По данным, приводимым в графике (начиная с исходного события на рис. 5), в таблице. заполняют графы 1—4. Чтобы не допустить ошибки, каждую работу, вписанную в таблицу, следует перечеркнуть в графике. Когда работы, выходящие н> исходного события, вписаны и перечеркнуты, в таблицу внося" работы, выходящие, из любого другого события, в которое не входят неперечеркнутые работы (теперь зтк события являются как бы исходными). Затем определяют [c.93]
Процесс создания технических систем и сложных объектов изображается в виде ориентированного графа, называемого сетевым графиком. [c.63]
Определение Т(Рун и ГРР для сетевого графика, приведенного на рис. 4.5, дано в табл. 4.3, представляющей собой часть табл. 4.2. При заполнении табл. 4.3 ранний срок начала работы, выходящей из исходного события, принимается равным нулю и проставляется в графе ТР." во всех стро- [c.69]
Расчет поздних сроков начала и окончания работ для сетевого графика, приведенного на рис. 4.5, дан в табл. 4.4, являющейся частью табл. 4.2. Для определения Т находим в графе ТР° значения для работ, которые заканчиваются конечным событием графика, и наибольшее значение переносим в графу Т в строки, [c.70]
Расчет сетевого графика с помощью теории графов. В качестве примера рассмотрим расчет сетевого графика, приведенного на рис. 4.5. [c.73]
Для выполнения расчета сетевого графика с помощью теории графов заполняется матрица связей между событиями. Матрица связей (рис. 4.И, о) представляет собой шахматную таблицу с числом столбцов и строк, равным количеству событий в сетевом графике. На пересечении /-и строки и t -ro столбца проставляется ожидаемое время выполнения. работы между f-м и /-М событиями. [c.73]
При исследовании сетевых систем можно полезно использовать ориентированные (направленные) графы. Такие графы показывают направление течения процессов. Их узлы изображают переменные параметры (х) системы, [c.32]
Для расчета критического пути и оптимизации сетевых графи- [c.384]
Если подготовка производства имеет (.-ложный характер и большую длительность, целесообразно построение сетевого графа. Он представляет собой графическое изображение комплекса всех параллельно и последовательно выполняемых работ, связанных с разработкой и внедрением новых средств и способов (рис. 5.2). [c.48]
Сетевой граф имеет исходную точку и замыкается на событии, являющемся конечной целью всех работ по данному проекту. Отдельные виды работ на графе обозначаются стрелками, а результаты их (события) — кружочками. Время, необходимое для выполнения работ (обычно в неделях), указано цифрами над стрелками. Жирными стрелками показан критический путь, определяющий максимальную продолжительность выполнения комплекса работ. Работы, лежащие на других путях, обычно располагают резервами времени. [c.48]
В процессе разработки и внедрения новых средств и способов сетевой граф корректируется. Благодаря сетевым графам руководители проектов обеспечиваются своевременной информацией и могут осуществлять непрерывный процесс [c.48]
Рис, 5.2. Сетевой граф выполнения работ [c.48]
В графу 2 запишем коды всех работ, входящих в сетевой график, в следующем порядке — сначала записываются все работы, выходящие из исходного (первого) события, затем из второго, третьего и т. д. до конца. В графу 3 записываются продолжительности этих работ. До начала расчета в графе 1 проставляется число работ, предшествующих данной. Это можно сделать, используя график или коды работ. Во втором случае обращаем внимание на первую цифру кода рассматриваемой работы (первая колонка), затем ищем эту цифру во второй колонке по направлению вверх от данной работы. Если искомая цифра встретилась только 1 раз, то данной работе предшествует только одна работа, если — 2 раза, то две работы и т. д. Например, возьмем работу 4—6. Цифра 4 в правой колонке кода работ, расположенных в табл. 4 выше работы 4—6, встречается 2 раза, значит работе 4—6 предшествует две работы. [c.50]
Расчет последующих ранних начал и окончаний производится с учетом того, что tim (/, k)=tpo (i, /). Например, для того чтобы рассчитать раннее начало работы 3—5, находим в графе кодов работ 2, выше работы 3—5, предшествующую ей работу, которая оканчивается на цифру 3 (работа 1—3). Значение ее раннего окончания, записанное графе 5, проставляем в графу 4 против 3—5, так как ро(1—3)= рн(3—5). Для работ, имеющих две и более предшествующих работы (например, работы 4—7), раннее начало берется максимальное из ранних окончаний предшествующих работ. Работе 4—7 предшествуют работы 2—4 и 3—4 с ранними окончаниями /ро(2—4) =7 и ро(3—4) = 11. Следовательно, в качестве раннего начала работы 4—7 принимаем наибольшее значение, т. е. 11, и проставляем его в графу 4 против работы 4—7. Одновременно заполняем и раннее окончание работы 4—7 как сумму его раннего начала и продолжительности самой работы 11+6 = 17. Таким образом, определяют ранние начала и окончания для всех работ сетевого графика. [c.51]
Кроме того, по объему и степени детализации различают первичные, частные и комплексные сети. Детализация графика для отображения в нем отдельных работ зависит от сложности разработки и продолжительности выполнения самих работ. Как правило, в сетевых графи- [c.220]
Графа 10 я II заполняются при оптимизации сетевых моделей. [c.18]
В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде ориентированного графа. Граф — это схема, состоящая из заданных точек (вершин), соединенных определенной системой линий. Отрезки, соединяющие вершины, называются ребрами (дугами) графа. Ориентированными называются такие графы, на которых стрелками указаны направления всех его ребер (дуг). Их исследование проводится с помощью методов теории графов. [c.35]
Под проектом (комплексом операций) будем понимать совокупность операций (работ), необходимых для достижения некоторого результата эти операции связаны между собой порядком их выполнения. Тогда проект может быть представлен сетью (или, как еще говорят, сетевым графиком или графом). Сеть дает наглядное изображение логических связей между работами. Главными элементами сети являются события и работы. События могут интерпретироваться как результаты выполнения промежуточных задач. События отражают как бы отдельные этапы выполнения проекта. Работа (операция) — это протяженный во времени процесс, необходимый для перехода от одного события к другому. [c.180]
Сетевыми методами планирования и управления условно называются методы планирования, основывающиеся на теории графов и теории вероятностей. Теория графов представляет собой учение о геометрических схемах, называемых графами. Прикладное значе- [c.133]
Сетевой график представляет собой ориентированный граф. Он состоит из кружков (колец) и соединяющих их линий (стрелок). Такой график представляет собой сеть, отсюда название самого метода. [c.137]
| Рис. 2. Схема формирования многоуровневой имитационной сетевой модели (однонаправленный граф в виде | 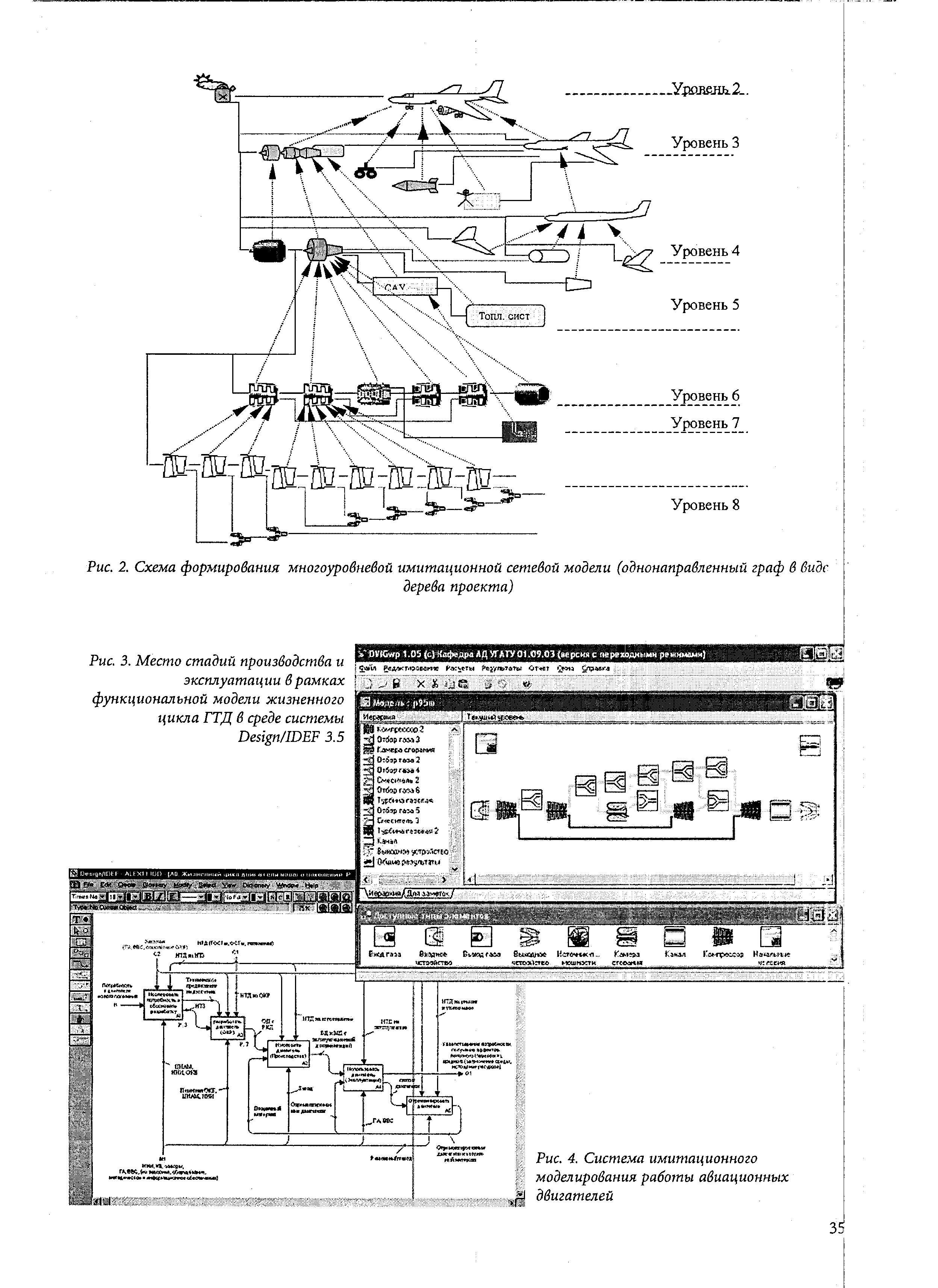 |
В этом случае задача ставится как сетевая транспортная, т. е. ее условия моделируются специальным графом или сетью. Принципы построения этой сети следующие. Выделяется ц -й вид транспорта, отражающий трубопроводный или другой подобный ему (с точки зрения принятых в задаче условий) транспорт. Сама сеть распадается на ( + ) подсеть, где R — число рассматриваемых продуктов. Каждая из первых 7 подсетей соответствует одному из продуктов и отражает процесс транспортировки этого продукта всеми видами транспорта (кроме ц -го) от пунктов отправления к пунктам потребления, включая перевалку этого продукта с одного вида транспорта. на другой. Последняя (7 +1)-я подсеть отображает возможность перевозки [c.69]
Соответствующая задача сводится к сетевой транспортной задаче с дополнительными ограничениями (,СТЗ ДО), где условия СТЗ полностью определяются сетью (графом) задачи, а дополнительные ограничения формируются по информации о связующих дугах. При этом число дополнительных ограничений равно (А —1)7, где / — число цепочек в (7 + 1)-й подсети. Для решения возникающей задачи могут быть использованы специальные алгоритмы и программы решения СТЗ ДО. Следует подчеркнуть, что в этих алгоритмах существенно используется структура матрицы СТЗ ДО, т. е. на каждой итерации операции преобразования обратной матрицы строятся в соответствии с методом потенциалов решения СТЗ. [c.70]
Соответствующая задача рассматривается также, в сетевой постановке, причем граф ее состоит из R (по числу продуктов) подсетей, каждая из которых отображает возможность перевозки одного из продуктов всеми без исключения видами транспорта. Задача сводится к СТЗ ДО, где граф определяет условия СТЗ, а в качестве дополнительных ограничений выступают ограничения пропускных способностей на отдельных коммуникациях. [c.71]
Сетевые модели и стохастические графы [c.184]
Использование сетевых моделей в практике управления нововведениями может принести значительный экономический эффект, который выражается в сокращении сроков и объемов затрат за счет улучшения координации и организации работ всех участников процесса создания новой продукции, рационализации использования ресурсов. Сетевые методы облегчают работу по созданию нормативной базы для последующего планирования нововведений, поскольку при их использовании накапливается статистический материал, который после обработки и проведения системного анализа может стать основой системы информационной поддержки принятия управленческих решений в области нововведений. В то же время стохастическая природа процесса создания и внедрения сложных инноваций, которая проявляется как в неопределенности нормативных затрат и сроков выполнения работ, так и в наличии в процессе разработки ситуаций, носящих случайный характер, требует введения в сетевой модели новых логических отношений. Действительно, сетевые графики адекватно описывают лишь детерминированные процессы. Более широкими возможностями отражения внутренней и внешней неопределенности продуктовых нововведений обладают стохастические графы. [c.194]
Стохастический граф G(I, U) с возможным возвратом в отдельных фрагментах проекта на доработку строится в несколько этапов. Сначала строится сетевой график G(Id, Ug). При этом считается, что такой сетевой график соответствует [c.196]
Таким образом, стохастический характер и цикличность процесса выполнения комплекса работ по освоению новой продукции обусловливают адекватность его отображения с помощью имитационной модели, основанной на графе с возвратом. Для графа с возвратом вводится ряд специфических временных параметров, часть из которых представляет собой развитие соответствующих характеристик сетевого планирования. Раннее время наступления события I — это время, необходимое для попадания из начального события в событие i в последний раз при движении по наименее благоприятному пути с учетом наступления возврата. Раннее время наступления конечного события графа совпадает с критическим временем реализации всего проекта. Позднее время наступления события i — это время наступления события i в последний раз, превышение которого приведет к увеличению критического времени. [c.196]
Алгоритм анализа графа с возвратом основан на использовании метода статистических испытаний и известного алгоритма Форда для сетевых графиков. Процедура Форда используется для расчета временных параметров отдельных фрагментов графа с учетом их топологии и задаваемых характеристик, а методами Монте-Карло имитируется реализация соответствующих дуг возврата. Таким образом, центральной процедурой алгоритма является моделирование событий контроля и согласования методом статистических испытаний. Исходы этих событий описываются вероятностями повторного исполнения определенных фрагментов проекта. [c.197]
Сетевая модель комплекса работ, выступая в системе СПУкак инструмент планирования и оперативного управления производством, представляет собой асимметричный, ориентированный слева направо граф, который состоит обычно из стрелок и кружков стрелками обозначают работы, кружками — события, т. е. результаты работ (рис. 5). [c.86]
Основными признаками при формировании очередности является соблюдение методического, логического, организационного и информационного единства. В качестве инструментария, используемого для увязки и контроля хода проектирования задач комплекса, может быть рекомендована оптимизация моделей на сетевых графах с учетом имеющихся ресурсов, выделенных на проектирование. Нормативная основа функционирования в службе управления персоналом САОИ должна быть зафиксирована в соответствующих методических и регламентирующих документах организации. В них должны быть сформулированы общие положения и содержание задач, реализованных в автоматизированном режиме, инструкции пользователям по решению отдельных задач, описание форм входных и выходных документов. [c.321]
Особое внимание при построении сетевое модели обращается на нумерацию событий (вершин графа). При нумерации событии обычно руководствуются оледущвмв сюновннми правилами [c.16]
Работа Ж И вДУ посладоватвдьво а работой в сетевом графа изображаются в виде "девочка" работ. [c.17]
Графа 2 заполняется досле окончательной нумерации событий в сетевой модели. со [c.18]
Графически такая взаимосвязь между счетами представляет собой сетевой граф. Внутри графа показывается код корреспондирующего счета, а левая и правая стороны графа указывают саму корреспонденцию счетов, ориентируясь по направлению стрелки. Направление стрелки с указанием номера хозяйственной операции идет от кредитуемого счета к дебетуемому. [c.168]
Использование сетевых методов, т. е. теории графов и теории вероятности в планировании и управлении, облегчает установление связей между исполнителями сложного комплекса работ, способствует обозримости всех ее частей, выявлению и устранению особо напряженных участков ( расширение узких мест ), позволяет осуществлять плановое прогнозирование и анализ хода выполнения работ и обнаруживать отставание на решающих участках работы. [c.134]
Решение возникающей задачи может быть осуществлено при помощи алгоритмов решения СТЗ ДО (однако их применение требует дополнительного обеспечения специальными приемами связности графа задачи) и алгоритмов, учитывающих блочный характер матрицы СТЗ. В статье [12] рассмотрены соответствующие модификации алгоритма К. В. Кима и известного метода декомпозиции. Вычислительные аспекты рассмотренных сетевых задач обсуждаются в статье [16]. В частности, соответствующие графы могут иметь большую размерность вследствие многократного дублирования (по числу продуктов) вершин и дуг исходной транспортной сети, однако на практике существует возможность существенного уменьшения этой размерности. В статье даются сравнительные оценки этих моделей для случая, когда возможно применение их обеих. Результаты весьма огра--ниченного эксперимента показали некоторую предпочтительность более частной модели. [c.71]
Выбор наиболее предпочтительных стратегических альтернатив осуществляется с использованием как формальных, так и качественных методов (интуиция руководителей, их видение путей реализации стратегии, представление о возможности реализации определенных альтернатив с учетом ограниченности ресурсов предприятия, поставленных целей и т. д.). Выбранные стратегические альтернативы, далее, конкретизируются в виде целевых программ с различными сроками реализации. При формировании целевых программ могут быть использованы сетевые графики или более сложные по структуре стохастические графы с возвратом, которые позволяют отобразить все взаимосвязи работ программы и смоделировать ход ее выполнения. Следует отметить, что конкретизация стратегических альтернатив является многоитерационным процессом, в ходе которого могут быть переосмыслены цели развития, может появиться новый взгляд на проблемы и как результат произойти изменение структуры программы. [c.186]
Логическую схему деятельности по разработке решения можно представить как блок-схему решени смыслового моделирования в виде графа. Вершины графа соответствуют этапам разработки решения ними. При этом граф представляет собой связное и логически обоснованное описание последов решения с учетом причинно-следственных связей между его этапами. Для отражения последовате работ при подготовке решений может использоваться и сетевое моделирование. [c.62]
