Опишем рассматриваемую газотранспортную сеть произвольной конфигурации (древообразной или многокольцевой) ненаправленным графом / (Х,7"), где X и Т непустые множества вершин и дуг соответственно. Вершинам графа ставятся в соответствие узлы системы, а дугам - газопроводные участки и компрессорные станции. [c.29]
Логически связанным с методом дерева целей является матричный метод, основанный на использовании матриц, отражающих значения (веса) вершин графа объекта прогнозирования с последующим преобразованием матриц и оперированием с ними. [c.29]
Понять в полной мере задачи интеграции разных методов статистического изучения связей можно с помощью графа связей. Граф связей учитывает непосредственные, т. е. причинные связи, которые предполагают изменение х/ при изменении влияющего на него X при постоянстве всех прочих факторов. Асимметричность причинных связей отражается в направленности дуг графа (дуга -соединение вершин графа, т. е. точек, соответствующих элементам структуры). [c.408]
Большими кружками (вершинами графа) на схеме показаны счета (каждый обозначен своим кодом), ребра схемы иллюстрируют движение средств. Каждое ребро пронумеровано в порядке их движения [c.56]
В простейшем случае рассмотрение может быть сведено к системе из двух элементов проект и организатор. Подобная схема приведена на рис. 2.1, вершины графа изображены прямоугольниками, а дуги помечены названиями денежных потоков. Под "проектом" в данной схеме понимается достаточно сложная система, которая включает в себя производственные мощности проекта, трудовые ресурсы, поставщиков, подрядные организации, покупателей продукции проекта и другие элементы, которые необходимы для организации производства и сбыта продукции проекта. Все эти элементы удобно объединить в одну систему, называемую "проект", и уже для нее производить оценку денежных потоков. [c.41]
Решение идет двумя каналами 1-й — преобразование матрицы, 2-й — построение графа. Решение начинается с сопоставления множества х (вершина графа) и нижней границы w(x), равной сумме всех понижений матрицы (оператор 2). [c.86]
Понижения строк, столбцов и всей матрицы Т представлены в табл. 23. Величину Р(Т) сопоставим вершине графа Г да(л ) = = Р(Т). Граф представлен на рис. 18. [c.95]
Оцениваем каждое календарное расписание (/=- , ------, т) и сопоставляем оценки вершинам графа. [c.117]
Определим (п+1)-вершинный граф с вершинами О, 1, 2,. .., п. [c.27]
Рассмотрим (п+1)-вершинный граф, соответствующий решаемой задаче (см. [c.128]
Шаг 1. Построим множество PJ, как множество вершин графа, [c.27]
Шаг 2. Строим множество / 2 всех вершин графа, связанных с PI [c.27]
Введем в рассмотрение и-вершинный граф Ga(y ), веса дуг в [c.40]
Множество терминальных вершин графа G обозначим TG. [c.28]
QG(g ) = h heV,(h,g )e E обозначено множество вершин графа G, из [c.56]
Введем в рассмотрение n-вершинный граф Ga(y), веса дуг в котором [c.54]
Установим следующее смысловое значение вершин графа G [c.122]
В вершинных графах или сетевых моделях типа работы-вершины (РВ) работы проекта представляются узлами (вершинами), а их взаимосвязи отражаются с помощью сплошных стрелок. К одному из преимуществ вершинных графов следует отнести отсутствие в них фиктивных (логических) работ. На рис. 3 показаны альтернативные представления одних и тех же фрагментов взаимосвязей работ с помощью стрелочных и вершинных графов. На этих фрагментах нетрудно убедится в преимуществах вершинных графов. [c.7]
| Рис. 3. Сравнение представлений схем выполнения работ с помощью стрелочных и вершинных графов Другим преимуществом сетевых моделей типа РВ или вершинных графов является возможность использования различных взаимосвязей работ (рис.4) | 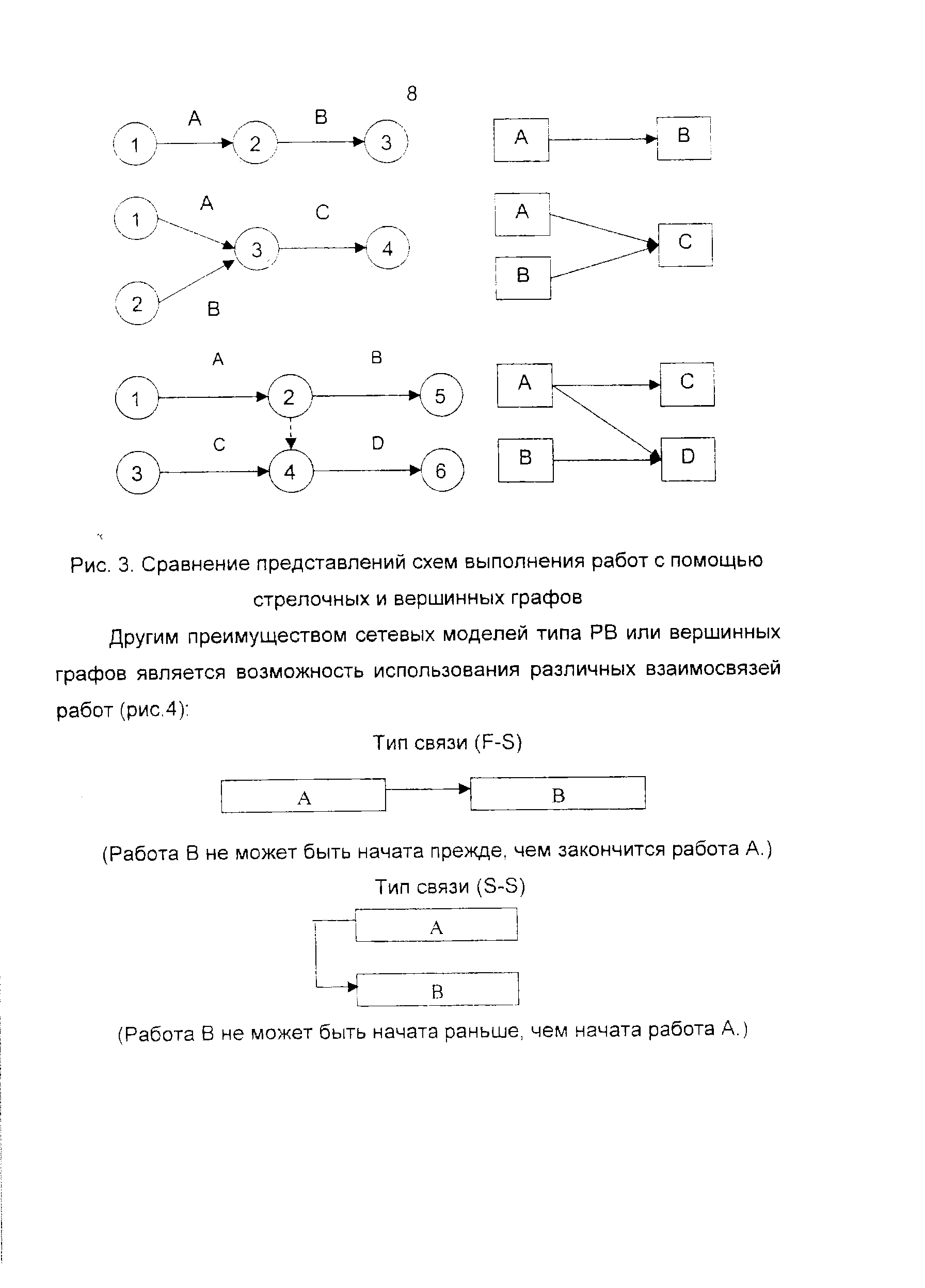 |
Деятельность предприятия, которое реализует проект, протекает в условиях взаимодействия с государством, которое получает от него налоги и другие обязательные платежи. Поэтому система на рис.2. 1 должна быть дополнена еще одним элементом - государством. Выгглата налогов является обязанностью предприятия, поэтому между вершинами графа, соответствующих предприятию и государству, нужно добавить дугу, которая должна отображать денежные потоки, связанные с уплатой налогов (см. рис. 2.2). Часто вместо элемента "проект" рассматривают более сложную систему "проект и его налоговое окружение" [3, 19], которая объ- [c.42]
Матрице В ставится в соответствие информационный граф G=(D,Rg). Множеством вершин графа G=(D,R0) является множество D информационных элементов, а каждая дуга (de d) соответствует условию dR0dj, т.е. записи 1 в позиции (if ) матрицы В. [c.137]
Разработанный в Московском институте управления им. Серго Орджоникидзе алгоритм моделирования задачи кустования, экономически поставленной НИПИНефтехимавтоматом, основан на теории объединения в группы объектов, имеющих общие информационно-технологические задачи. В качестве информационно-технологической характеристики использованы показатели территориальной близости и производственной связи. Модель структуры представлена в виде графовой модели. Это позволяет сформулировать задачу как экстремальную. Все территориальные управления представлены в виде множества вершин графа. [c.14]
Логическую схему деятельности по разработке решения можно представить как блок-схему решени смыслового моделирования в виде графа. Вершины графа соответствуют этапам разработки решения ними. При этом граф представляет собой связное и логически обоснованное описание последов решения с учетом причинно-следственных связей между его этапами. Для отражения последовате работ при подготовке решений может использоваться и сетевое моделирование. [c.62]
