Понять в полной мере задачи интеграции разных методов статистического изучения связей можно с помощью графа связей. Граф связей учитывает непосредственные, т. е. причинные связи, которые предполагают изменение х/ при изменении влияющего на него X при постоянстве всех прочих факторов. Асимметричность причинных связей отражается в направленности дуг графа (дуга -соединение вершин графа, т. е. точек, соответствующих элементам структуры). [c.408]
Методика комплексного использования индексного и регрессионного анализа такова. Определяется жестко детерминированное уравнение связей у = f(xt,..., дгт), на основе графа связей строится уравнение регрессии для каждой компоненты (х) [c.409]
| Рис. 1.1. Граф связей между уровнями временных рядов во время t |  |
Структурные модели позволяют не только оценить непосредственное и полное влияние переменных, но и прогнозировать поведение системы, определять расчеты значения эндогенных переменных. Если же такая задача не ставится и имеется лишь потребность в уточнении характера связей переменных, то эффективным является применение путевого анализа ( -анализа). Уже в самом названии этого метода отражается активное использование графа связей, изоморфного системе уравнений. [c.214]
| Рис. 4.1. Граф связи между у и хх | 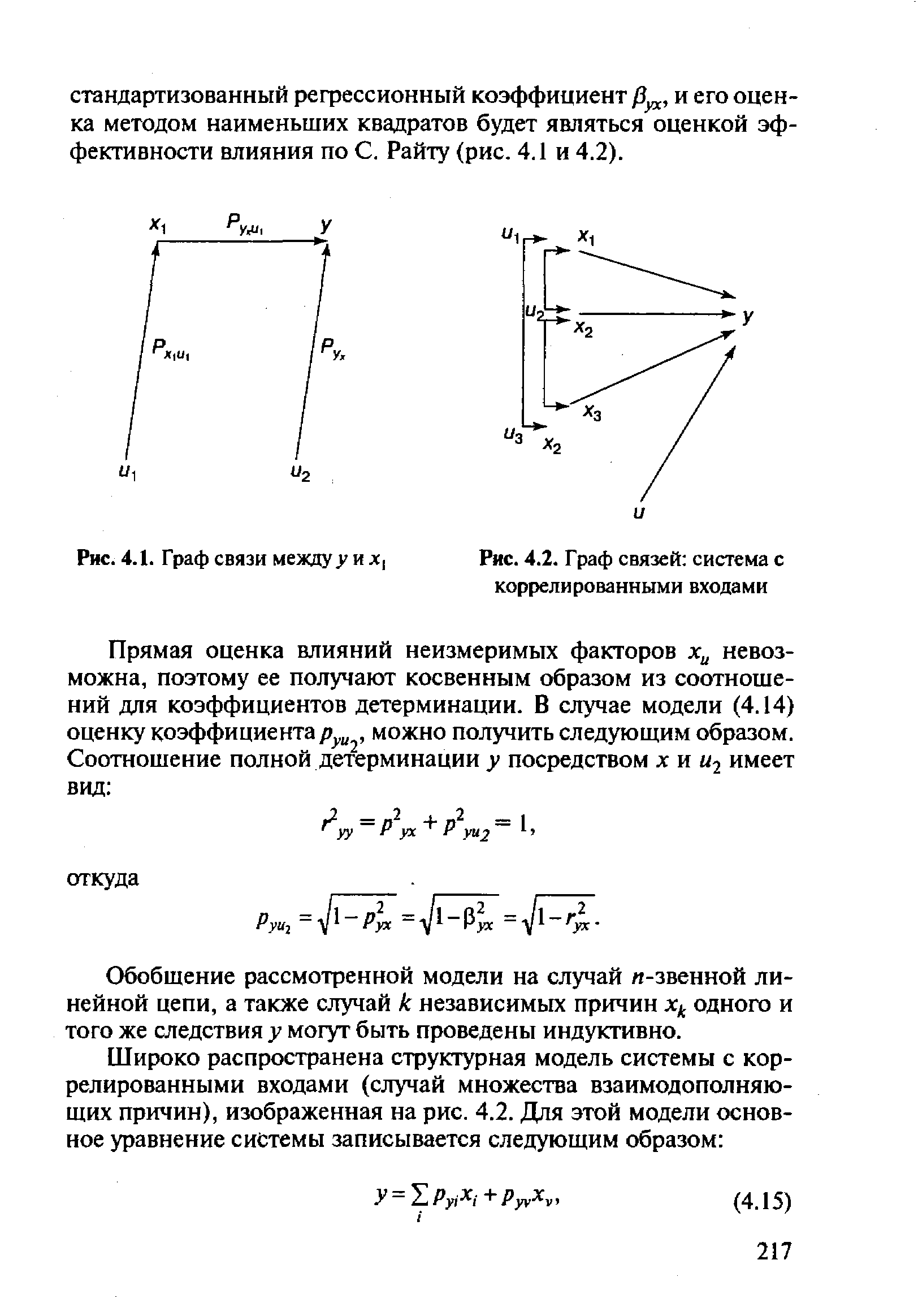 |
| Рис. 4.2. Граф связей система с коррелированными входами | 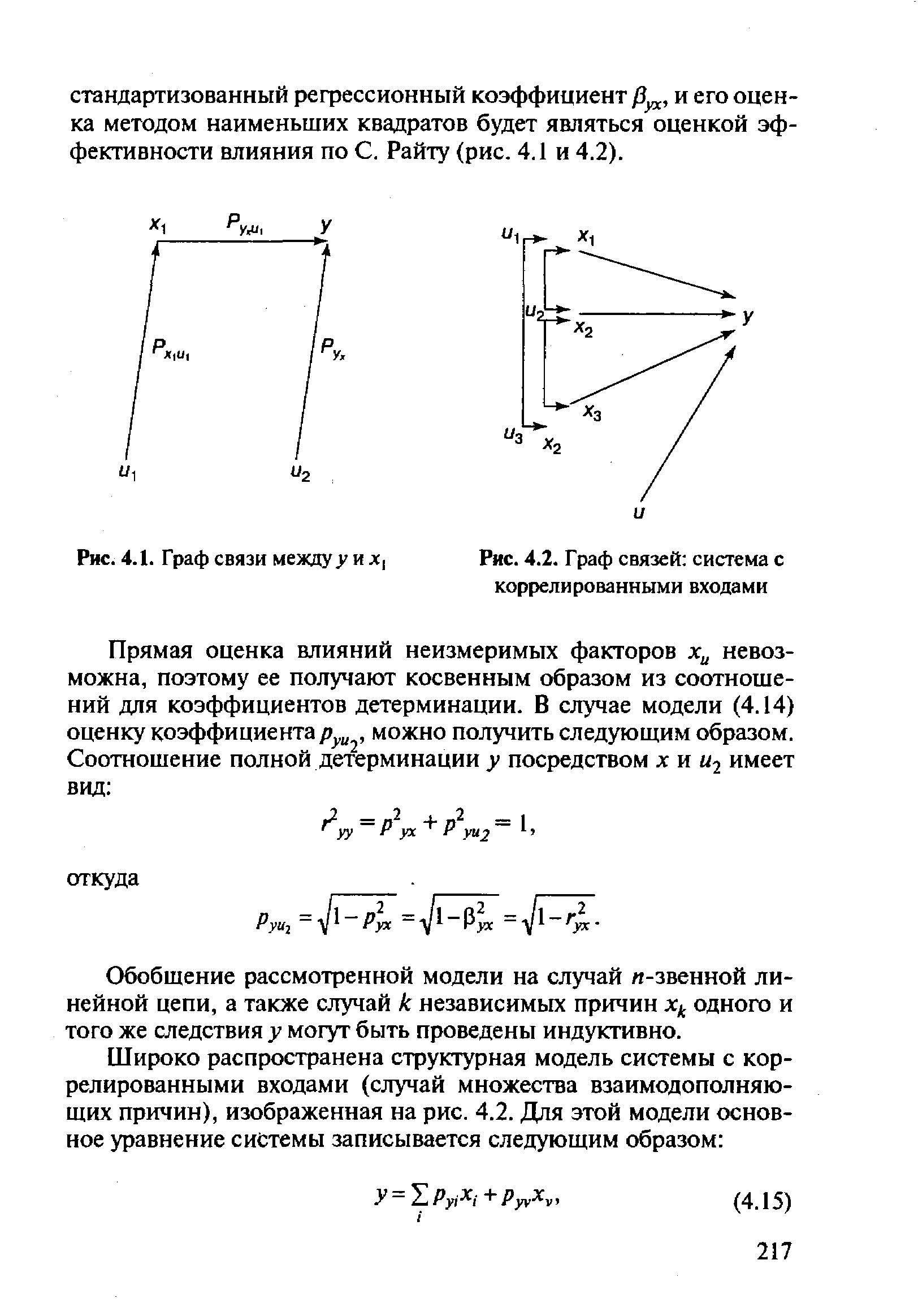 |
Гарвардский барометр 10-11 Гармонический анализ 12-13 Гетероскедастичность 24, 162-166 Гомоскедастичность 156,160-162 Граф связей 18,213-214 [c.338]
Выделение и раздельный анализ системы параметров со связями первого и второго типа необходимы. Как мы увидим, в дальнейшем, при переходе от анализа одного типа связей к другому должен меняться метод анализа, и, кроме того, анализ связей второго типа представляет самостоятельный интерес. Действительно, пусть имеется некоторая группа параметров, каждый из которых входит хотя бы в один >кон-тур и пусть попарно параметры имеют очень тесную связь. Тогда изменение хотя бы одного из этих параметров повлечет за собой изменения всех параметров. Исходя из этого можно выбрать такую относительно немногочисленную группу параметров, с помощью которой можно будет управлять изменчивостью всех параметров. Более того, если мы придем к решению о том, что некая группа параметров обязательно должна изменяться лишь взаимосвязанно, и экспериментально подтвердим это, мы сможем построить такую систему связей внутри данной группы параметров, чтобы каждый параметр входил в заранее заданный контур. Частичный граф максимальной размерности графа связей, каждая из вершин которого входит в какой-либо контур, будем называть автоматом. [c.23]
Рассмотрим, сначала круг задач, решение которых не связано с изменением множества вершин (построение графа связей, каждая из которых должна быть непосредственной -выявление взаимосвязанных параметров, прямых структур и автоматов). Для краткости в этом случае мы будем писать, что задан граф G(U). Обозначим через ji// множество путей от вершины xi к вершине х . Таким образом, каждой паре вершин (xi, х ,) графа G(U] можно поставить в соответствие множество [г 7. Некоторый частичный граф для исходного графа G(U) обозначим G(U ). Каждой паре вершин (xi, Xj) графа G(U ) ставится в соответствие множество путей fi//. Частичный граф G(U ) назовем допустимым для [c.24]
Множество вершин, не входящих ни в один автомат, образуют прямые структуры. В случае если граф связей содержит автоматы, для получения минимального графа в исходном графе к каждому автомату применяется операция стягивания всех вершин в одну. Минимальный граф строится [c.34]
Наконец, решим задачу, связанную с исключением части параметров из графа связей. [c.35]
Исходный граф связей описывается следующей матрицей смежности (см. табл. 1). Выделим прямые структуры, автоматы и взаимосвязанные характеристики. Для нахождения автоматов получим максимальный граф с соответствующей матрицей смежности (см. табл. 2). Характеристики ,2, 5, 13, очевидно, не входят в автоматы, так как [c.36]
Найдя пересечение четвертой строки с четвертым столбцом в матрице смежности максимального графа, обнаруживаем, что вершины 4, 7, 8, 9, 10, 11, 12 принадлежат одному автомату. После вычеркивания строк и столбцов с номерами 1, 2, 4, 5, 7, 8, 9, 10, 11, 12, 13 получим такую матрицу смежности (см. табл. 3). Пересечение строк и столбцов этой матрицы указывает на отсутствие автоматов. Таким образом, граф связей имеет лишь один автомат, описываемый следующей матрицей смежности (см. табл. 4). [c.36]
По тем или иным причинам не всегда необходимо или возможно продолжать исследование тех характеристик, по которым вначале строился граф связей. При большой размерности графа связей для дальнейшего анализа можно вы- [c.41]
Введем обозначения V — объем производства цемента в год F — среднегодовые размеры основных фондов N—численность производственных рабочих. В соответствии с нашими рассуждениями справедлив следующий граф связей (см. рис. 12). [c.74]
Пусть Д1/ — часть выпуска цемента, которая обеспечивается рабочими, не связанными с основными фондами, AAf — часть численности рабочих, не обеспеченных основными фондами, и V = V—AF N = N—АЛ/". Отсюда мы получаем новый граф связей (см. рис. 13). [c.74]
Стороны, и средней маркой цемента и вводом добавок, с другой стороны, очень малы (0,0768 и —0,1531 соответственно). Низки и соответствующие коэффициенты регрессии. Следовательно, можно попытаться построить уравнение регрессии без учета этих параметров в расчете на несущественность снижения множественного корреляционного отношения. На эту же возможность указывает и граф связей (см. рис. 15). [c.141]
Из графа связей видно, что параметр 4 является по отношению к остальным параметрам независимым, а влияние параметров 2 и 3 опосредуется параметром 1. [c.141]
Матрица смежности максимального графа связей будет иметь следующий вид (см. табл. 81). [c.142]
Вернемся вновь к нашему примеру. Из матрицы смежности максимального графа связей следует, что системой, в которой отсутствуют причинные связи, является система переменных х , хв, и х-,. Следовательно, их взаимосвязи мы можем характеризовать с помощью коэффициентов корреляции. [c.147]
Задана матрица смежности графа связей В — = II г/ kxk- [c.151]
Коэффициентам влияния присущи те же недостатки и они имеют ту же формальную трактовку, что и частные коэффициенты корреляции, с тем явным преимуществом перед последними, что коэффициенты влияния есть функция не только связи, но и структуры связей множества параметров. С другой стороны, это преимущество несколько ослабляется, поскольку само построение структуры графа связей не формализовано. [c.156]
В задаче анализа улова рыбы мы находим следующий граф связей [c.159]
В,табл. 93 приведены парные коэффициенты корреляции. Для исследования влияния числа тралений на улов рассмотрим граф связей (см. рис. 29). [c.185]
Изучаемую систему представляют в виде иерархии, которая изображается графом связей (в простейшем случае типа дерево) между элементами уровней - первый и очень важный этап решения задачи. [c.253]
Нередко оказывается, что разобраться в системе связей можно только тогда, когда граф связей будет включать не только факторы - признаки данной единицы совокупности, непосредственно определяемые в процессе ее функционирования (эндогенные), но и факторы, не зависящие от нее, но влияющие на изучаемый результат (экзогенные). Если первые образуют систему признаков и могут находиться в жестко детерминированной связи с изучаемой результативной переменной вследствие устойчивости связи в рамках единицы совокупности, то вторые не являются признаками изучаемой единицы, потому их связь с результатом неустойчива, стохастична. Как правило, действие экзогенных факторов опосредовано эндогенными переменными, формирующими результат. Потребность сочетания разных уровней анализа - вышележащего , на котором могут иметь место жестко детерминированные связи, и нижележащего , на котором они отсутствуют, вызывает интеграцию разных методов анализа. Например, изучая, почему произведен тот или иной объем валовой продукции, весьма важно не останавливаться на анализе уравнения связи, подобного приведенному в п. 10.7, включающего признаки, определяемые на уровне предприятия, а перейти на другой уровень анализа. Выявить, например, чем обусловлена та или иная величина среднечасовой вы- [c.408]
На рис. 10.2 изображен гипотетический граф связей, в котором элементы высшего уровня структуры обозначены какxf (/ = 1,2,..., т). Это факторы, находящиеся в жесткой связи с результатом (у) z, - глубинные факторы, принадлежащие другому уровню изучаемой структуры связей (/ = 1,2,. ..,z). Эти факторы находятся в стохастической связи с xf- и у. [c.409]
Методы корреляций и регрессий создавались как методы описания совместных изменений двух и более переменных. Совместные изменения переменных могут не означать наличия причинных связей между ними. Потребность в причинном объяснении корреляции привела американского генетика С. Райта к созданию метода путевого анализа (1910—1920) как одного из разновидностей структурного моделирования. Путевой анализ основан на изучении всей структуры причинных связей между переменными, т. е. на построении графа связей и изоморфной ему рекурсивной системы уравнений. Его основным положением является то, что оценки стандартизированных коэффициентов рекурсивной с истемы уравнений, которые интерпретируются как коэффициенты влияния (путевые коэффициенты), рассчитываются на основе коэффициентов парной корреляции. Это позволяет проанализировать структуру корреляционной связи с точки зрения причинности. Каждый коэффициент парной корреляции рассматривается как мера полной связи двух переменных. [c.18]
Для формальной верификации гипотез необходимо соответствие между графом и системой уравнений, его описывающей. Алгебраическая система, соответствующая графу без контуров (петель), является рекурсивной системой, позволяющей рекур-рентно определять значения входящих в нее переменных. В такой системе в уравнения для признака xt включаются все переменные, за исключением расположенных выше его по графу связей. Формулировка гипотез в структуре рекуррентной модели обычно не вызывает затруднений при использовании данных в динамике. Если же анализируются статистические данные, то следует учитывать зависимость системы от ее прошлых состояний. [c.213]
Систему (4.14) можно представить в виде графа связей (рис. 4.1). Встает вопрос об оценке коэффициентов р руиг Коэффициент корреляции случайных переменных хну как первый смешанный момент нормированных случайных величин определяется соотношением [c.216]
Структурные причинные модели в эконометрике и социологии соединяют теорию объекта с эмпирическими данными на основе графа связей. Структурные модели формализуют гипотезы о причинных отношениях. Встает задача выбора гипотез, обозначаемая иногда в эконометрической и социологической литературе как проблема каузального вывода. Х.Блейлок, изучая этот вопрос как часть общего вопроса о средствах построения социологических теорий, предложил формальный прием, основанный на идеях Г.Саймона о ложной корреляции и каузальной упорядоченности, иногда называемый процедурой Саймона — Блейлока. [c.222]
Использование /ьанализа в социально-экономических исследованиях связано с рядом трудностей. Прежде всего не всегда можно считать, что линейная зависимость в состоянии удовлетворительно отразить все разнообразие причинно-следственных связей в реальных структурах. Кроме того, следует учитывать, что />-анализ разработан для количественных переменных. Структурные модели и путевой анализ иллюстрируют единство теоретического (качественного) и формально-математического (количественного) подходов. Значимость результатов анализа определяется в первую очередь правильностью построения логического каркаса структурной модели — максимально связанного графа связей, изоморфной математической модели в виде системы уравнений. [c.223]
Постановка задачи в- этом случае должна начинаться с выбора характеристик процесса и анализа структуры их связей. Поскольку в обычных задачах число переменных большое и поскольку правильнее с методической точки зрения начинать постановку задачи с учета максимально возможного количества характеристик (эта необходимость будет доказана далее), словесный анализ структуры связей рак-тйчески невозможен. Возникает необходимость формального представления структуры связей. Для этого предлагается использовать аппарат теории графов.Такой подход позволит каждой изучаемой системе параметров ставить в соответствие определенную логическую структуру, формализуемую некоторым графом. В результате появляется язык для строгой и компактной записи качественных знаний. Необходимость составления гипотетического графа связей обязывает исследователей проводить более глубокий анализ1 изучаемых явлений. [c.20]
Задача о минимальном и максимальном графах связей и о числе допустимых графов решена Ф. В. Монни в работе Об одной, экстремальной задаче из теории графов , опубликованной в сборнике статей Опыт решения экономических задач математическими методами . Новосибирск, 1967. [c.24]
Мы попытаемся теперь более основательно подойти к определению графа непосредственных связей, максимального графа связей и к статистической оценке связей, указываемых этими графами. Идея построения подобных графов заимствована у У. Р. Эшби [34.91—92]. Граф непосредственных связей в этой работе называется схемой непосредственных воздействий, а максимальный граф связей— схемой конечных воздействий. Схему непосредственных воздействий, У Р. Эшби определяет следующим образом Для того чтобы найти непосредственные воздействия в системе с переменными А, В, С, D..., нужно взять одну пару,, скажем А и В поддерживать все остальные переменные С, D. .. на постоянном уровне отметить поведение В, когда А имеет начальную величину Alt а также тогда, когда эта величина равна А 2. Если поведение В в обоих случаях одинаково, то Л не оказывает на В никакого непосредственного воздействия. Но если поведение В различно и закономерно меняется в зависимости от начальной величины А, то непосредственное воздействие существует, что можно обозначить А- -В. Меняя местами Л и В в этой процедуре, мы можем затем проверить наличие связи В- А. Испытывая поочередно дру- [c.150]
Решение задачи. Граф связей вначале разбивается на слои . Первый слой образуется множеством вершин, принадлежащих входу графа. Внутри слоя вершины пронумеровываются числами от 1 до /. Если теперь от графа отсечь вершины входа вместе с инцидентными им дугами, to в полученном частичном графе множество вершин его входа образует второй слой. В нем верщинам присваиваются номера от / + 1 до /2. Продолжая указанный процесс, мы разобьем весь граф на какое-то число слоев. Ясно, что в графе без контуров каждая вершина будет принадлежать какому-либо слою и количество слоев не будет превышать количество вершин в графе. [c.151]
Теперь предположим, что структура причинно-следственных связей, зафиксированная графом связей, верна, т. е. соответствует реальной структуре. Пусть верна и гипотеза о форме связей между каждыми двумя факторами, находящимися в причинно-следственных отношениях. Введем понятие замкнутости графа связей. Для этого выскажем следующую гипотезу, которую по-видимому, аналитически доказать невозможно два процесса, имеющих либо общую причину, либо общее следствие, стохастически зависимы. То же касается и показателей, отражающих эти процессы. Эта гипотеза кажется естественной, поскольку процессы, имеющие общую причину или общее следствие, должны протекать согласованно. Примем за истинное и обратное утверждение любые стохастически зависимые во времени процессы либо имели общую причину, либо будут иметь общее следствие. Под общей причиной мы понимаем некоторый процесс или группу процессов, существенно определяющих изменчивость изучаемых процессов во времени, а [c.173]
