Матрица смежности — квадратная матрица по числу ИО. Матрица заполняется по строкам. Элемент матрицы на пересечении строки и столбца равен 1, если ИО, стоящий в строке, связан с ИО, стоящим в столбце, отношением один ко многим, тип функциональной связи во внимание не принимается. Таблица 7.1 соответствует матрице смежности для ИО ИЛМ примера 2. Несколько однотипных структурных связей двух ИО рассматривается как одна (например, Счет, Субсчет — Шаблон, Счет, субсчет — ЖХО — представлены однократно). [c.523]
Q вычислить итоговые суммы элементов матрицы смежности по столбцам [c.524]
Q удалить строки матрицы смежности, соответствующие ИО текущего уровня иерархии [c.524]
Формализованно связи (парные отношения) между наборами информационных элементов отображаются в виде матрицы смежности В, под которой понимают квадратную би-136 [c.136]
В позиции ( i,j ) матрицы смежности записывают 1 (т.е. q . = 1 ), если между информационными элементами dfu (/.существует отношение R0, такое, что для получения значения информационного элемента d. необходимо непосредственное обращение к элементу d.. Наличие такого отношения между dt и d. обозначают виде d.R0d., чему соответствует д.. =1, а отсутствие - d. RQ d., т.е. q.. = 0. Для простоты принимают, что каждый информационный элемент недостижим из самого себя [c.137]
Например, задано множество ) из четырех наборов информационных элементов, т.е. D- dr d2, d , d4 . Пусть матрица смежности В этих элементов имеет вид [c.137]
Для описания графа G построим матрицу смежности (табл. 22), которая для неориентированного графа имеет вид А = ац , где ау — элементы матрицы смежности, определяемые следующим образом [c.105]
По матрице смежности определим ранг каждого элемента [c.106]
| Таблица 22 Матрица смежности | 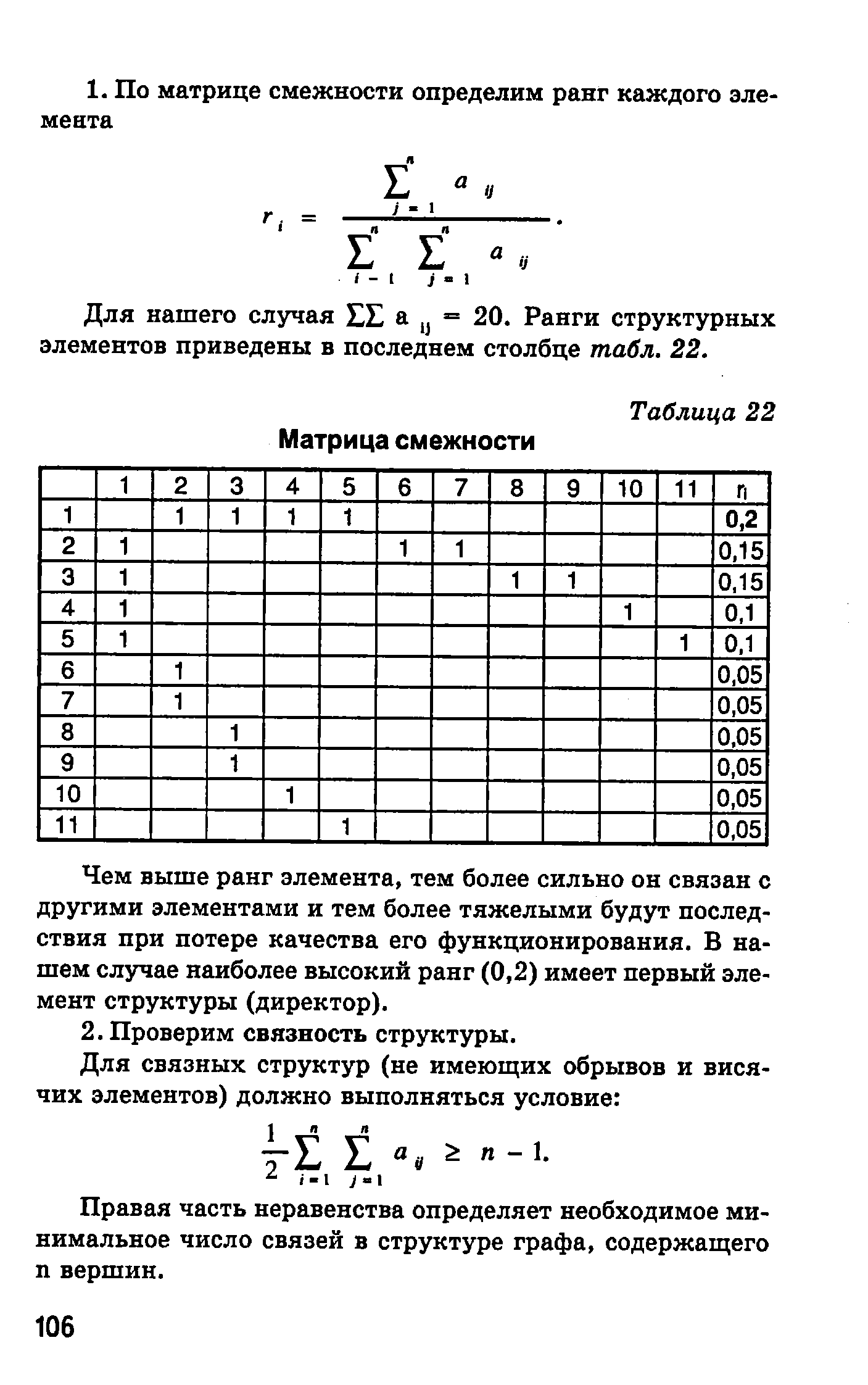 |
На основе систем сравнений по факторам были построены квадратные матрицы смежности, в которых на персональном компьютере вычислялись значения относительных приоритетов по каждому фактору планирование ассортимента производимой продукции система сбыта формирование ценовой политики реклама инновационная деятельность предприятия система стимулирования работников комплекс взаимоотношений с общественностью (табл. 24.2). [c.489]
Для выполнения формальных преобразований и постановки прикладных задач удобна матричная форма задания графов. Полную информацию о графе дает матрица смежности вершин (матрица репрезентативности графа). Это квадратная матрица размерности х п, в которой единицы ставятся на пересечении /-х строк иу-х столбцов для всех дуг (у)е А. Остальные клетки матрицы содержат нули. Если граф ориентированный, то вершинам /, называемым вершинами-предками, соответствуют строки матрицы, а вершинам j, называемым вершинами-потомками, — ее столбцы. Матрица смежности вершин графа, заданного с помощью рис. 4.9, показана в табл. 4.1. [c.122]
| Таблица 4.1 Матрица смежности вершин графа |  |
Обозначим множество всех допустимых графов для исходного через F, матрицу. смежности некоторого допустимого графа < ( / ) через А = а (i, j = 1,. ... k). [c.25]
Минимальным, графом для исходного назовем такой допустимый граф G(U), для матрицы смежности которого А = ajj (/. / = 1,. .., k) выполняется условие [c.26]
Определение 4. Пусть граф G(U) задан матрицей смежности А = а,Л d, / = 1.....k), а граф G(V)—матри- [c.27]
Пусть,. например, граф G(U) задан матрицей смежности [c.28]
Тогда матрица смежности графа G (S) = G (U) G (V) [c.28]
Нетрудно заметить, что, если графы принадлежат классу графов с матрицами смежности, подчиняющимися условию (1), действия, введенные определениями 1—5, не выводят графы за пределы того же класса. [c.29]
Замечания. Если некоторый граф G(U) задан матрицей смежности А = а,-/ (i, / = 1,. .., k , граф G(V) — матрицей смежности Z == zi/ (i, / = 1,. .., k), то [c.29]
Матрица смежности графа G (S), являющегося суммой G(U) и G(V), [c.29]
Матрица смежности графа G(S ), являющегося разностью G(U) и G(V) (для определенности положим U V), [c.29]
Матрица смежности графа G(S ), являющегося пересечением графов G(lf) и G(F), [c.29]
Теорема 1. Пусть G (U) — исходный граф с матрицей смежности Л, В — матрица смежности "k — степени [c.29]
Для G(U) всегда существует единственный минимальный граф G(U) с матрицей смежности А = А — А х Г. [c.30]
Пусть задан некоторый исходный граф G (U) с матрицей смежности Л = Оу[[ (i, / = 1,. .., k). В алгоритме все элементы матрицы А мы будем называть исходными. [c.30]
Замечание. Пусть В — матрица смежности X — степени графа G(U) и С = S Вх (X =-1,. .., k — 1). Тогда Л=1-(1+С)-1 где 1—единичная матрица. 30 [c.30]
Обозначим множество всех поглощающих графов для исходного графа через Т, матрицу смежности некоторого поглощающего графа G(V) — через В = btj (i, / = 1, . . . , k). Пусть max 22 bi,=b0(i, /= 1,. .., k). [c.33]
Максимальным графом для G (U) назовем такой поглощающий граф G (V), для матрицы смежности которого В = .у. (/, /= 1,. .., k) выполняется условие 2S btJ- = [c.33]
Теорема 3. Для исходного графа G((J) всегда существует единственный граф G(V) с матрицей смежности [c.33]
Пусть задан некоторый граф с матрицей смежности А = au (i, /= 1,. .., k). [c.33]
Получим максимальный граф G (У) с матрицей смежности в = 2 ля, (х = ь - ) [c.34]
Простые задачи (расчет одной или нескольких таблиц), а также работы с матрицами смежности при выборе хранимых данных могут быть запрограммированы с помощью электронных таблиц (например, Ex el), что фактически является элементом автоматизации этапов технического и рабочего проектирования. [c.346]
Рассмотрим теперь формальное решение этих задач1. Пусть задан граф G (X, U). Каждой характеристике некоторого процесса ставится во взаимооднозначное соответствие вершина графа, каждому влиянию — одна дуга. Такой граф может быть записан матрицей смежности [c.24]
Определ ениеб. Пусть граф G(U) задан матрицей смежности А = ац (i, j = 1,. .., k). Граф G(A). с матрицей смежности В будет называться Я — степенью графа G(U), если Вх = 11 Ь = лх (г, / - 1,. .., k), где возведение в степень выполняется по определению 4. [c.28]
Матрица А называется нильпотентнои, если существует такое целое число О <г <оо, что Аг — 0. Пусть граф G (X, U) задан матрицей смежности С = сц (i-j == 1,..., к), не обязательно удовлетворяющей условию (1). Если матрица С нильпотентна, граф G (X,U) называется нильпотентным. [c.29]
Пусть задан некоторый граф G (X, U) с матрицей смежности А = at) (i, /= 1,..., k). Назовем вершины i и / смежными, если ау- -а >0. Пусть из графа G(X, U) должно быть исключено некоторое множество вершин х вместе с инцидентными им дугами. В результате мы будем иметь частичный граф G(X, U ) (X Х U /L/) с матрицей смежности А -— а / , i, j X x. Пусть вершины, принадлежащие х, смежны -некоторому множеству вершин S X x. Через sfir Обозначим множество путей, соединяющих вершины г, t S и проходящих через вершины / лс, через u t — дугу в графе G(X, U ), соединяющую вершины г, t S. Граф G (X, И ) будем называть сокращенным для G(X, U), если из n-rjt=f= iS следует, что urt — 1 для всех г, t S и / х. [c.35]
Смотреть страницы где упоминается термин Матрица смежности
: [c.523] [c.523] [c.345] [c.46] [c.107] [c.107] [c.189] [c.473] [c.137] [c.28] [c.28] [c.34]Экономико-математический словарь Изд.5 (2003) -- [ c.67 , c.189 ]
