Хотя на графике обычно просматривается тенденция к некоторой упорядоченности, может оказаться невозможным соединить точки прямой. По точкам диаграммы рассеяния можно построить две линии линию регрессии х по у и линию регрессии у по х. Они совпадут, если имеет место точно линейная зависимость этого не произойдет в противном случае, но мы пользуемся здесь понятием корреляции, а не функциональной зависимости. [c.187]
Как уже отмечалось, главным условием повышения конкурентоспособности товаров и организации является повышение качества. Например, ведущие западные компании затрачивают миллиарды долларов на программу шесть сигм 1) таблица случайных событий 2) Г-тесты 3) планирование эксперимента 4) регрессионный анализ 5) диаграмма Парето 6) статистические методы контроля качества продукции (диаграмма рассеяния, контрольные карты). Реализация программы шесть сигм направлена на снижение уровня дефектности до 3, 4 дефектов на 1 млн изделий. [c.469]
Для установления силы влияния (корреляции) одного фактора на другой и направленности взаимодействия строят корреляционные поля (диаграммы рассеяния) — рис. 17.8. Анализ рисунка показывает, что связь между Х и Y тесная, прямолинейная, [c.473]
| Рис. 17.8. Корреляционные поля (диаграммы рассеяния) | 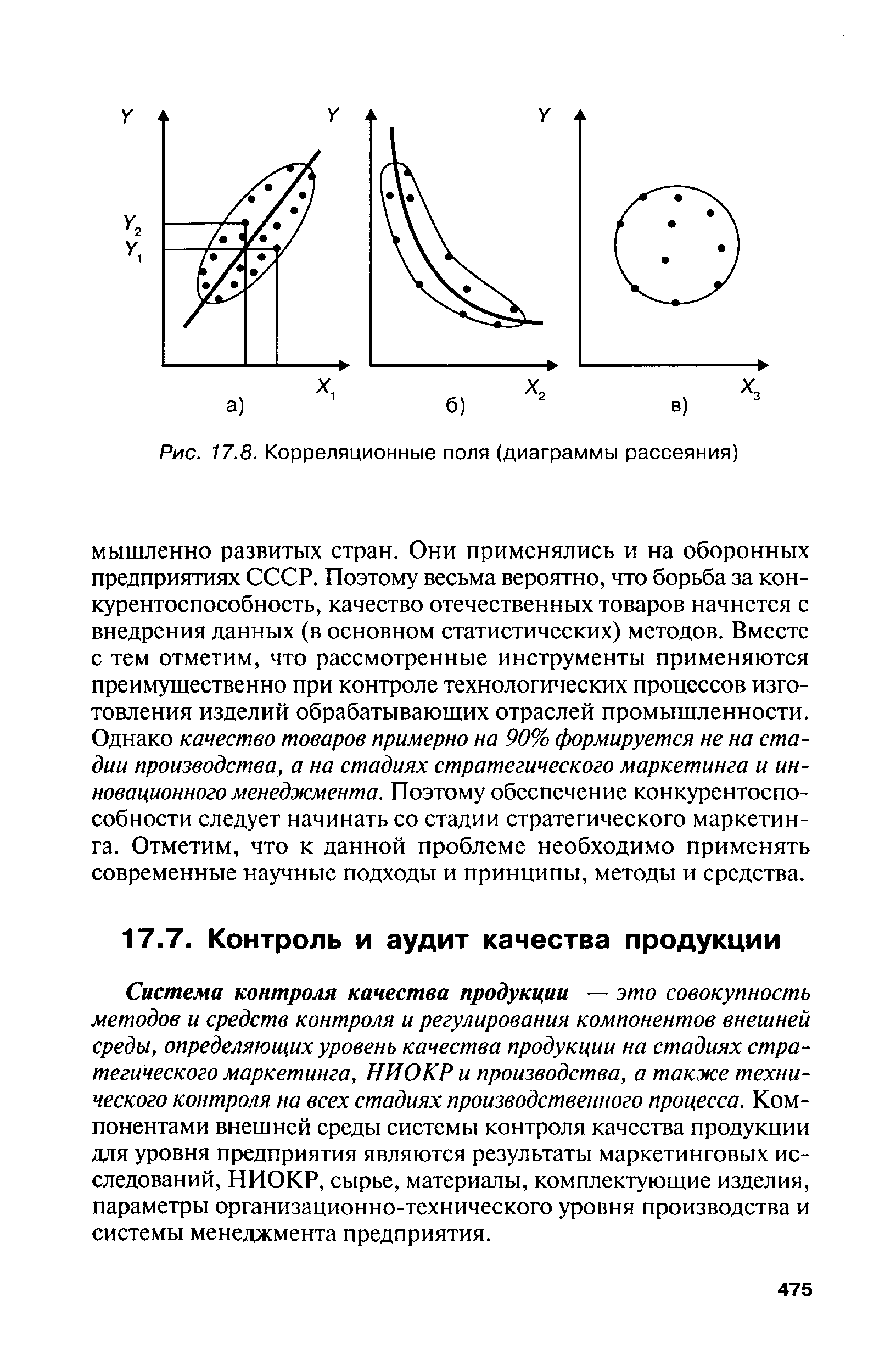 |
Рисунок 2-5 служит также примером диаграммы рассеяния. [c.33]
О Диаграмма рассеяния — это график, показывающий значения пары экономических переменных для различных экономических единиц или временных периодов. [c.33]
Диаграммы рассеяния дают наглядное представление о том, существует ли четкая связь между двумя рассматриваемыми переменными. [c.34]
Временные ряды также могут быть изображены в виде диаграммы рассеяния. Рисунок 2-6, например, показывает часть недавней картины изменений в инфляции и безработице, которую экономисты и политики пытались понять в 1978 г. Одна точка соответствует значениям пары переменных годового темпа инфляции (для измерения уровня цен использовался дефлятор ВНП) и годового темпа роста реального ВНП в том же году. Каждая из 10 черных точек соответствует одному году из периода 1958-1967 гг. каждая из 10 цветных точек одному году из периода 1968-1977 гг. Рассмотрение изображенного на рисунке 20-летнего периода как целого не позволяет выявить существенной связи между этими двумя переменными, особенно если исключить две точки (два года) с наивысшим значением темпа инфляции (это 1974 и 1975 гг. — результат повышения мировых цен на нефть в конце 1973 г. в 4 раза). Но рисунок явно подсказывает интересный результат получается, что независимо от того, [c.34]
Графики экономических данных, в частности диаграммы рассеяния, используются для выявления трендов, структуры и возможных связей между экономическими переменными. Для характеристики взаимосвязей между экономическими переменными с помощью чисел и уравнений применяются эконометрические методы. [c.37]
Относительные и реальные цены Процентные изменения Темп прироста Темп инфляции Временной ряд Пространственная выборка Диаграмма рассеяния Эконометрика [c.38]
Такая зависимость графически изображается в виде экспериментальных точек, образующих поле рассеяния, или, как принято говорить, поле корреляции (рис.26). Следовательно, такие двумерные данные можно анализировать с использованием диаграммы рассеяния в координатах <ос - у , которая дает визуальное представление о взаимосвязи исследуемых совокупностей. [c.14]
При анализе двумерной диаграммы рассеяния можно обнаружить различные взаимосвязи. Простейшим вариантом является линейная взаимосвязь, которая выражается в том, что точки размещаются случайным образом вдоль прямой линии. Диаграмма свидетельствует об отсутствии взаимосвязи, если точки расположены случайно, и при перемещении слева направо невозможно обнаружить какой-либо уклон (ни вверх, ни вниз). [c.14]
Если точки на ней группируются вдоль кривой линии, то диаграмма рассеяния характеризуется нелинейной взаимосвязью. Такие ситуации вполне [c.14]
На рис. 3.15 представлены диаграммы рассеяния полученных оценок темпов роста СФП с темпами роста ВРП. [c.154]
| Рис. 3.15. Диаграммы рассеяния темпов роста ВРП и оценок темпов роста остатка, полученных разными методами для 1997-2002 гг. |  |
| Рис. 772-7. Диаграмма рассеяния темпов роста выпуска и темпов роста различных факторов |  |
Диаграмма рассеяния для этих данных имеет весьма специфический вид [c.68]
Диаграмма рассеяния переменных xt,yt в нашем примере имеет вид [c.72]
Диаграмма рассеяния (поле корреляции). Поле корреляции — это графическое представление точек с координатами, определяемыми значениями двух переменных и зависимой), для всех наблюдений. [c.650]
Значения остаточных членов используют при вычислении некоторых статистик, связанных с регрессией. В дополнение к этому диаграммы рассеяния остатков, которые показывают их значения в зависимости от предсказанных значений времени или предикторов дают полезную информацию для анализа правильности сделанных допущений [c.665]
Множественная регрессия включает одну зависимую и две (или больше) независимых переменных. Частный коэффициент регрессии "представляет ожидаемое изменение ко гда меняется на одну единицу, а переменные от до остаются постоянными. Силу тесноты связи измеряют коэффициентом множественной детерминации Значимость общего уравнения регрессии проверяется общим Отдельные частные коэффициенты регрессии можно проверить на значимость, используя приращений. Диаграммы рассеяния остаточных членов, когда их значения представлены графически в зависимости от предсказанных теоретических значений времени или предикторов, полезны для проверки [c.678]
Аналогичная ситуация возникает на практике, когда мы располагаем п парами выборочных наблюдений X и У и можем изобразить их на плоскости с помощью такой же диаграммы рассеяния, как на [c.21]
Диаграмма рассеяния 21 Дискриминантная функция 336 Дискриминантный анализ 334 Дисперсионный анализ 43 Дисперсия оценки 30 Дифференцирование по вектору Доверительные интервалы 35, i [c.439]
ДИАГРАММА РАССЕЯНИЯ [s atter diagram] в математической статистике — диаграмма, на которой в прямоугольной системе координат располагаются точки (х., у у, где/= 1, 2,..., п, ии — количество наблюдаемых пар значений переменных х и у. (Примеры Д.р. см. в ст. "Корреляционный анализ ".) [c.82]
Расположив данные из табл. 6.1 на приведенной ниже точечной диаграмме рассеяния (рис. 6.1), мы действительно видим, что высокие (низкие) значения S P 500 соответствуют высоким (низким) значениям FTSE 100. Таким образом создается впечатление, что данные по двум индексам растут и падают вместе. [c.263]
В специальной литературе приводятся несколько вариантов набора инструментов качества. Например, в [7, 23] рассматривается семь инструментов качества метод расслоения информации по группам факторов, влияющих на качество процессов, графики, диаграммы Парето, причинно-следственные диаграммы (диаграмма Исикавы), гистограммы, диаграммы разброса, контрольные карты и контрольные листки. В этом же источнике приводятся семь дополнительных инструментов качества диаграммы сродства (сходства), диаграммы зависимостей, системные (древовидные) диаграммы, матричные диаграммы, сетевые графы, диаграммы планирования процессов, метод анализа матричных данных. В [23] приведены девять инструментов качества 1) построение схемы процесса 2) контрольный листок 3) мозговая атака 4) диаграмма Парето 5) причинно-следственная диаграмма (диаграмма Исикавы) 6) временной ряд 7) гистограмма 8) диаграмма рассеяния (корреляционное поле) 9) контрольная карта. [c.470]
Если диаграммы рассеяния могут быть использованы для обнаружения простых взаимосвязей между парами значений переменных, то эконометриче-ские методы используются для измерения и поиска более сложных зависимостей между экономическими переменными. Эти зависимости оказываются выраженными в виде чисел и уравнений. [c.34]
Диаграмма рассеяния темпов роста выпуска и темпов роста различных факторов (см. Приложение 2, рис. 772-7) свидетельствует о достаточно слабой связи между темпами роста ВРП и темпами роста затрат труда и капитала. Невысокий процент объясненного роста выражается в том, что структура оценок СФП практически повторяет структуру ВРП (см. рис. 3.13 . С одной стороны, это объясняется довольно приблизительными оценками затрат факторами, с другой - выбранным интерва- [c.135]
Самый распространенный метод для расчета уравнения линейной регрессии по данным на диаграмме рассеяния — это метод наименьших квадратов pro edure). [c.652]
Диаграмма рассеяния, поле корреляции, 650 йскринантная достоверность, 357 [c.948]
Если теперь мы произведем выборку п семей так, чтобы были представлены все уровни дохода от Хг до Х , то соответствующая выборка точек может быть изображена на диаграмме рассеяния (см. рис. 2.2). Когда значения и приближаются к независимым, точки выборки более или менее тесно группируются вокруг прямой линии. Это означает, что любое значение %, будь оно положительным или отрицательным, никоим образом не влияет на значения 2, 3> -Вместе с тем может случиться, что людьми с низкими доходами окажутся в основном молодожены, стремящиеся большую часть своих средств тратить на потребительские нужды, в то время как высокие доходы у пожилых членов общества, уже имеющих все необходимое. В таком случае мы можем ожидать положительные возмущения при малых значениях Л и отрицательные возмущения при больших.Отсутствие беспорядочности в возмущениях служит здесь индикатором того, что нами упущена такая важная объясняющая переменная, как возраст, включение которой в возмущающий член и привело к нарушению его беспорядочного (рандомизированного) поведения. [c.21]
Н диаграмме рассеяния (рис. 2.3) изображены перпенд шуляры, опу-т=зые из точки с координатами X и Y на оси координат. Мы хотим п ести линию через множество точек наблюдения, которая будет OL EKOH истинной линии а + рХ. Запишем..уравнени-- оцениваемой Л12 и в виде [c.23]
Предположим, что мы имеем выборку наблюдений Хг, Уг (i = I,. . ., п), которая представлена на диаграмме рассеяния (см. рис. 2.4). Разобьем диаграмму на четыре квадранта с помощью перпендикуля- [c.41]
Корреляцию моделируют С помощью графика XY (S atter, Точечный график, диаграмма рассеяния), выбирая подтип графика, который дает точечные образы данных (без линий). График моделирует связи двух переменных. Числовые данные блока двух [c.106]
