Изобразим полученную зависимость графически точками координатной плоскости (рис. 3.1). Такое изображение статистической зависимости называется полем корреляции. [c.53]
Корреляционная связь или ее отсутствие часто устанавливается графически, путем построения так называемого поля корреляции (рис. 1.5 и 1.6) [14]. [c.28]
Постройте поле корреляции и сформулируйте гипотезу о форме связи. [c.37]
При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рис. 2.1. [c.37]
Построение линейной регрессии сводится к оценке ее параметров — а и Ь. Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис. 2.2). Далее по графику можно определить значения параметров. Параметр а определим как точку пересечения линии регрессии с осью оу, а параметр b оценим, исходя из угла наклона линии регрессии, как dy/dx, где dy — приращение результата j>, adx — приращение фактора х, т. е. [c.41]
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора х, т. е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результату. Это равносильно тому, что коэффициент детерминации г2 будет приближаться к единице. [c.49]
Соответственно для зависимости, изображенной на полях корреляции рис. 3,5 б) и в), гетероскедастичность остатков представлена на рис. 3.9 и 3.10. [c.162]
| Рис. 3.9. Гетероскедастичность, соответствующая полю корреляции | 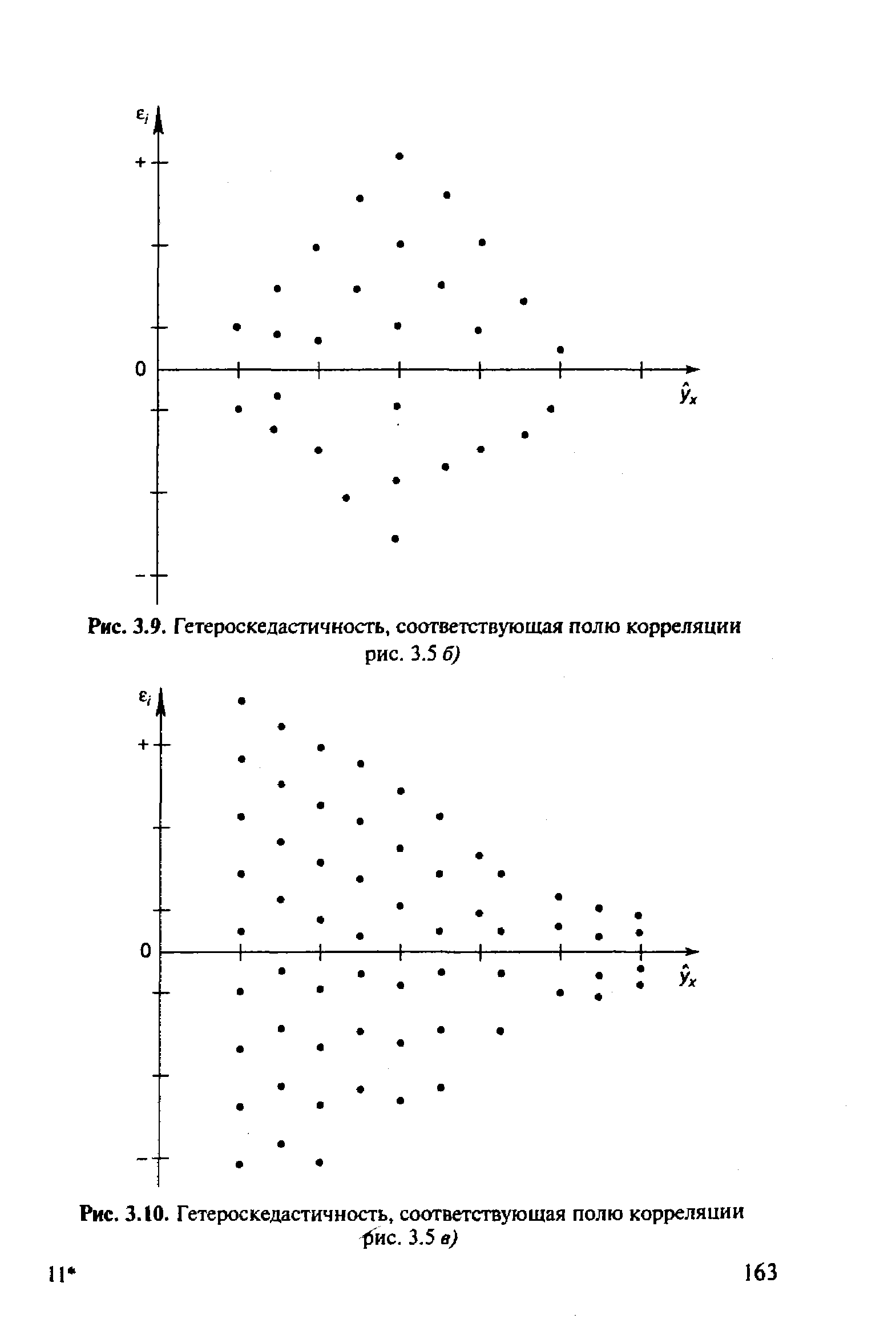 |
Если поле корреляции может быть аппроксимировано прямой, которая называется линией регрессии, то приступают к вычислению коэффициента парной корреляции г. Его числовые значения заключены в интервале [-1, 1]. Если г равно 1 или -1, то существует функциональная прямая или обратная связь. Когда г близок к нулю, связь между явлениями отсутствует, а при г 0,7 связь считается существенной. Коэффициент корреляции рассчитывают по формуле [c.222]
После выделения названных выше групп железнодорожных хозяйств был использован еще один приближенный прием предварительного анализа однородности совокупности по каждой группе железнодорожных хозяйств — построение полей корреляции каждого из включенных в исследование факторов с себестоимостью перевозок. Основным признаком однородности или неоднородности выбранных совокупностей служило отсутствие или наличие разрывов и скачков в расположении точек на полях корреляции. [c.111]
Для изучения были предварительно выбраны путем профессионального логического анализа все возможные факторы, данные об изменении которых по предприятиям имеются в отчетности министерства. Такими факторами следует считать общий объем перевозок, среднюю производительность вагонов и локомотивов рабочего парка, грузонапряженность, фондоемкость единицы перевозок и производительность труда и др. (всего 11 факторов). Таким образом, по четырем группам предприятий было построено 44 поля корреляции. [c.111]
Имеются и другие ошибки в расчетах себестоимости перевозок в мелких железнодорожных хозяйствах. Как следствие — она искусственно завышается в несколько раз. Поэтому мелкие железнодорожные хозяйства с объемом перевозок до 1 млн. т в год были исключены. С помощью такого искусственного приема удалось достигнуть относительной однородности в расположении точек на полях корреляции. Окончательный вывод об однородности выбранных совокупностей (групп) железнодорожных хозяйств можно сделать по характеру отклонений фактических значений себестоимости перевозок в каждом железнодорожном хозяйстве от рассчитанных по разработанным многофакторным моделям (уравнениям регрессии). [c.112]
После определения указанных величин получается уравнение парной зависимости, графическое изображение которого в осях координат называется теоретической линией регрессии. Если на такое поле нанести все замеры, а не только теоретическую линию регрессии, то мы получим поле корреляции. [c.122]
Исходный материал систематизируем на поле корреляции и в корреляционной таблице. В нашем примере в качестве фактора выступает стоимость машин См, а в качестве функции — среднегодовая численность рабочих Р. [c.135]
В результате разбивки на интервалы вся плоскость, на которой нанесены замеры по обоим признакам к и у, называемая полем корреляции, представит собой клетки, причем каждый замер характеризуется не точными значениями своих координат, а лишь значениями интервала, в который он отнесен. [c.136]
На рис. 16 представлено поле корреляции, на котором по оси абсцисс даны интервалы для значений аргумента Сы, а по оси ординат — интервалы для значения функции Р. Построенное таким способом поле корреляции называется вторичным. [c.136]
Для выбора интервалов может быть построено также первичное поле корреляции. Все точки на этом поле проставлены с учетом значений их координат. По густоте расположения точек и намечаются интервалы. [c.136]
Наряду с построением поля корреляции, как указано выше, составляется корреляционная таблица, в которой производятся все вычисления, связанные с определением средних, построением эмпирической линии регрессии и исходных данных для определения параметров в системе нормальных уравнений. [c.136]
В табл. 36 весь материал распределен по интервалам. Используя его, строим вторичное поле корреляции, на которое наносим все значения переменных, и определяем средние значении (/,, //,,. .., уп по интервалам. Соединив между собой средние значения в каждом интервале отрезками прямых линий, получаем эмпирическую линию регрессии (см. рис. 16). [c.136]
| Рис. 16. Корреляционная таблица и вторичное поле корреляции | 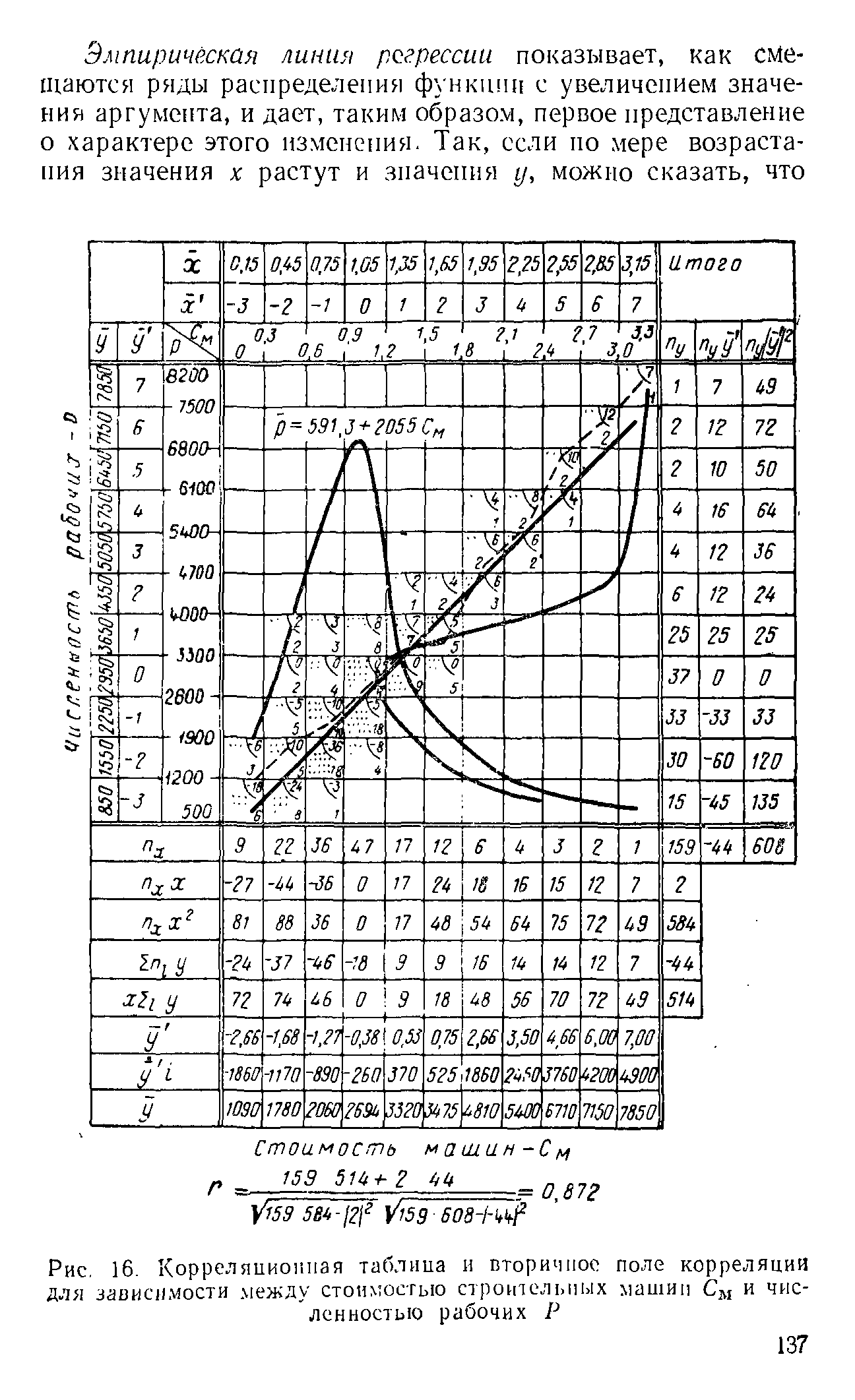 |
| Рис. 18. Корреляционная таблица и вторичное поле корреляции зависимости численности рабочих и объема применения сборных железобетонных конструкций | 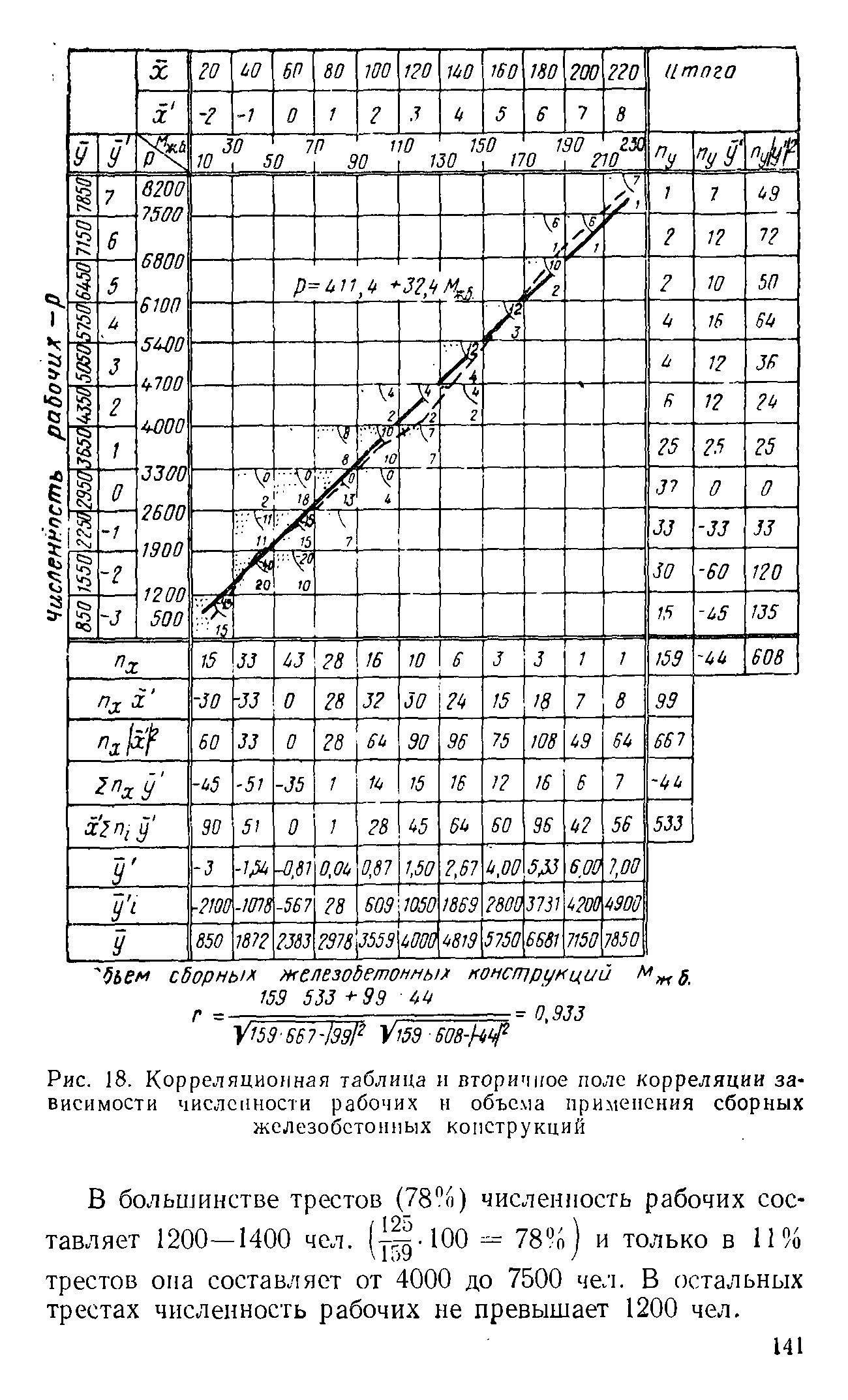 |
Такая зависимость графически изображается в виде экспериментальных точек, образующих поле рассеяния, или, как принято говорить, поле корреляции (рис.26). Следовательно, такие двумерные данные можно анализировать с использованием диаграммы рассеяния в координатах <ос - у , которая дает визуальное представление о взаимосвязи исследуемых совокупностей. [c.14]
Диаграмма рассеяния (поле корреляции). Поле корреляции — это графическое представление точек с координатами, определяемыми значениями двух переменных и зависимой), для всех наблюдений. [c.650]
Это графическое изображение точек с координатами, значениям двух переменных для случаев. Обычно значения зависимой переменной откладывают по вертикальной оси, в значения независимой — по горизонтальной. Поле корреляции используется при определении формы зависимости между переменными, График дает исследователю первое [c.651]
Метод, используемый для расчета параметров уравнения линейной регрессии, когда на основе поля корреляции минимизируются расстояния по вертикали всех точек поля от графика регрессии. [c.652]
Вариация данных анализируется с помощью полигона распределения, кумуляты (кривой меньше, чем ) и огивы (кривой больше, чем ). Все эти виды графиков рассматриваются в главе 5. Линейные графики используются в решении задач классификации данных (см. гл. 6). Применение линейных графиков в анализе динамики рассмотрено в главе 9, а использование их для анализа связей -в главе 8. В этих же главах рассмотрено использование точечных диаграмм (см., например, поле корреляции в гл. 8). [c.64]
В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора Xj остатки е,- имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастнчность. Наличие гетероскедастич-ности можно наглядно видеть из поля корреляции (рис. 3.5). [c.160]
Другая типичная исследовательская задача - оценка взаимосвязи между явлениями - решается с помощью хорошо разработанного в математической статистике аппарата теории корреляции. Для этого необходимо иметь выборки по сравниваемым явлениям, показанным на картах разной тематики (например, Д и В). Значения а и Ь, берут в одних и тех же /-х точках, т.е. строго скоординированно, и затем строят график поля корреляции. [c.222]
Смотреть страницы где упоминается термин Поле корреляции
: [c.303] [c.340] [c.28] [c.28] [c.32] [c.138] [c.143] [c.13] [c.15] [c.651] [c.651]Эконометрика (2001) -- [ c.37 , c.39 ]
