Диаграммы разброса

Теперь мы в состоянии сравнить ожидаемый доход по отдельной ценной бумаге с ожидаемым доходом на рыночный портфель. В нашем сравнении будет полезно учитывать доход, превышающий ставку по безрисковым ценным бумага. Рис. 5.3 иллюстрирует пример сравнения ожидаемого избыточного дохода по определенной акции с избыточным доходом на весь рыночный портфель. Жирная линия называется характеристической линией. Она показывает связь между избыточным доходом по акции и избыточным доходом на рыночный портфель. Эта связь может базироваться на данных о прошлых соотношениях, в этом случае избыточный доход по ценной бумаге и на рыночный портфель должен быть нанесен на график, а затем проведена линия, наилучшим образом аппроксимирующая имеющуюся информацию о динамике рассматриваемого соотношения в прошлом. Такая ситуация проиллюстрирована на диаграмме разброса значений, изображенной на рис. 5.3. Каждая точка представляет собой избыточный доход по акции и индексу S Р за один из 60 прошедших месяцев. Месячный доход должен в обоих случаях рассчитываться по схеме цена на конец периода минус цена на начало периода плюс дивиденды, деленные на цену на начало периода. Из этого дохода вычитается безрисковая месячная ставка, в результате чего получается избыточный доход.  [c.111]


Последняя из трех интересующих нас характеристик — это несистематический, или остаточный риск акции. Этот вид риска описывается разбросом оценок относительно характеристической линии акции. На рис. 5.3 он представлен относительным расстоянием до сплошной линии. Если бы все точки на диаграмме разброса лежали на характеристической линии, несистематический риск был бы равен 0. Весь риск был бы связан с общим рыночным риском. Если точки широко разбросаны вокруг характеристической линии — это показывает, что значительная часть риска связана с компанией-эмитентом акций. Чем больше разброс точек на рисунке, тем выше несистематический риск акции. Однако риск этого типа может быть сокращен посредством диверсификации акций в инвестиционном портфеле. Было доказано, что несистематический риск сокращается уменьшающимися темпами при увеличении числа различных акций в портфеле, постепенно приближаясь к нулевому значению. Таким образом, значительной доли несистематического риска акции можно избежать при сравнительно умеренной диверсификации вложений, когда число акций в портфеле колеблется от 15 до 20. Несистематический риск хорошо диверсифицированного портфеля приближается к нулю. Это может быть проиллюстрировано так, как показано на рис. 5.5. По мере увеличения числа случайно выбранных акций в портфеле суммарный риск портфеля сокращается за счет уменьшения несистематического риска. Однако темпы этого сокращения уменьшаются, что можно видеть на рисунке.  [c.114]


Минимаксный метод прост в использовании, но имеет недостаток, так как для оценки параметров выбираются две крайние точки, которые могут не соответствовать нормальным условиям работы, что может привести к некорректной оценке величин а и b в формуле. В рассматриваемом Случае 1 отрицательное значение а вызывает сомнения. В такой ситуации предпочтительнее опустить эти значения и выбрать две другие точки, которые лучше отражают реальную ситуацию. Для этого необходимо проверить диаграмму разброса.  [c.90]

Прежде чем реализовывать регрессионный подход с использованием метода наименьших квадратов, очень важно нанести данные на специальную диаграмму - так называемую диаграмму разброса (см. рис. 16.3). Это делается для того, чтобы убедиться в существовании линейной зависимости между значениями X и Y прошлых периодов.  [c.260]

Рисунок 16.3. Диаграмма разброса 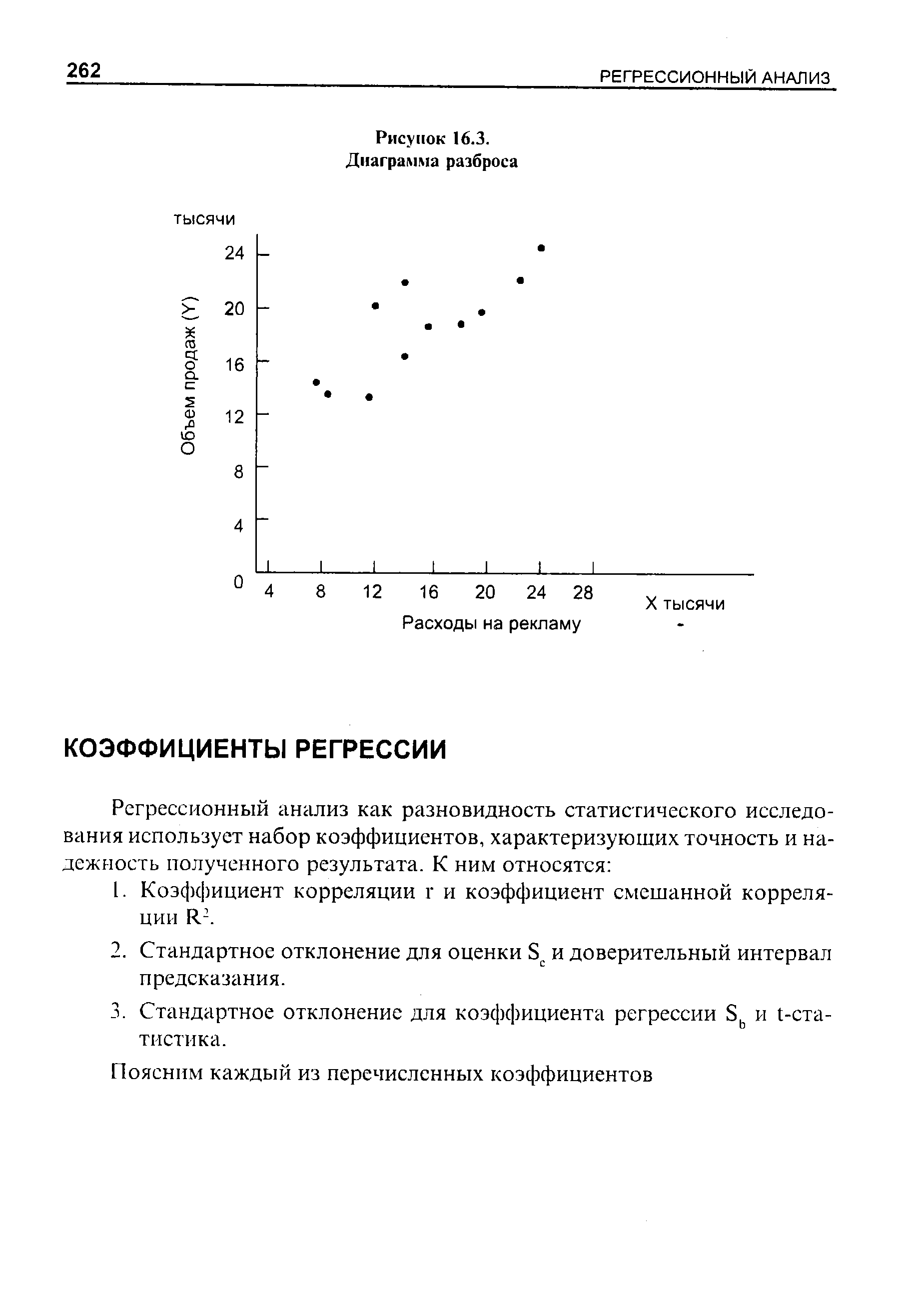Рисунок 16.3. Диаграмма разброса
R2 характеризует общее согласие (всего "леса" невязок на диаграмме разброса), в то время как t-значение характеризует отдельную независимую переменную (отдельное "дерево" невязок).  [c.267]

Диаграмма разброса (рассеивания) - это графическое представ-  [c.27]

Диаграмма разброса строится в таком порядке по оси абсцисс  [c.27]

Таким образом, диаграмма разброса позволяет визуально ус-  [c.29]

Элементарный статистический контроль использует карты Парето, причинно-следственный анализ, группировку данных по общим признакам, контрольные листы, гистограмму, диаграмму разброса, график и контрольную карту Шухарта.  [c.122]

Диаграмма разброса представляет собой график вида, приведенного на рис. 5.12-5.14. Диаграмма позволяет выявить корреляцию между двумя различными факторами.  [c.303]

Рис. 5.12. Диаграмма разброса взаимосвязи показателей практически нет Рис. 5.12. Диаграмма разброса взаимосвязи показателей практически нет
Рис. 5.13. Диаграмма разброса имеется прямая взаимосвязь показателей Рис. 5.13. Диаграмма разброса имеется прямая взаимосвязь показателей
Рис. 5.14. Диаграмма разброса имеется обратная взаимосвязь показателей 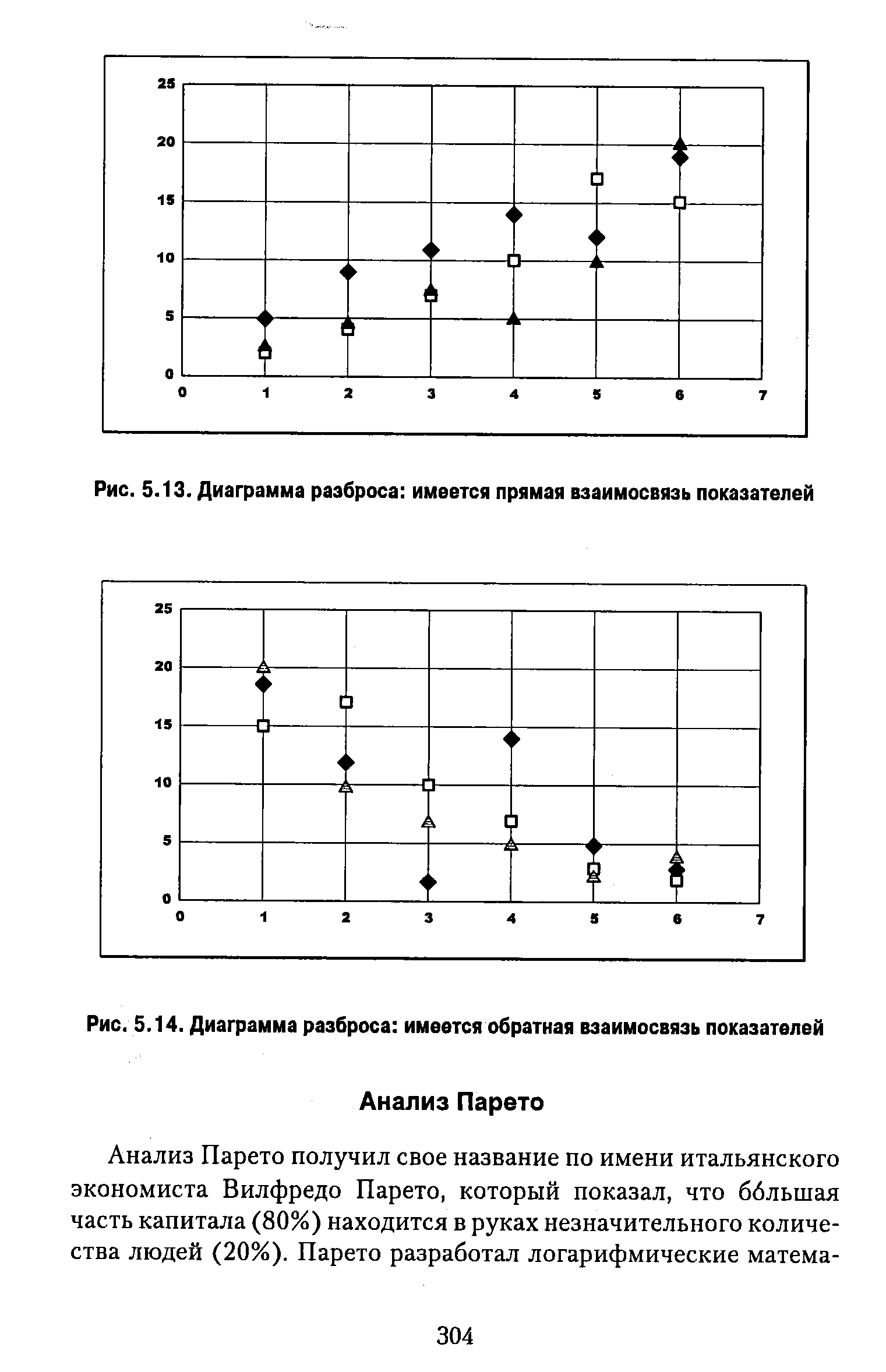Рис. 5.14. Диаграмма разброса имеется обратная взаимосвязь показателей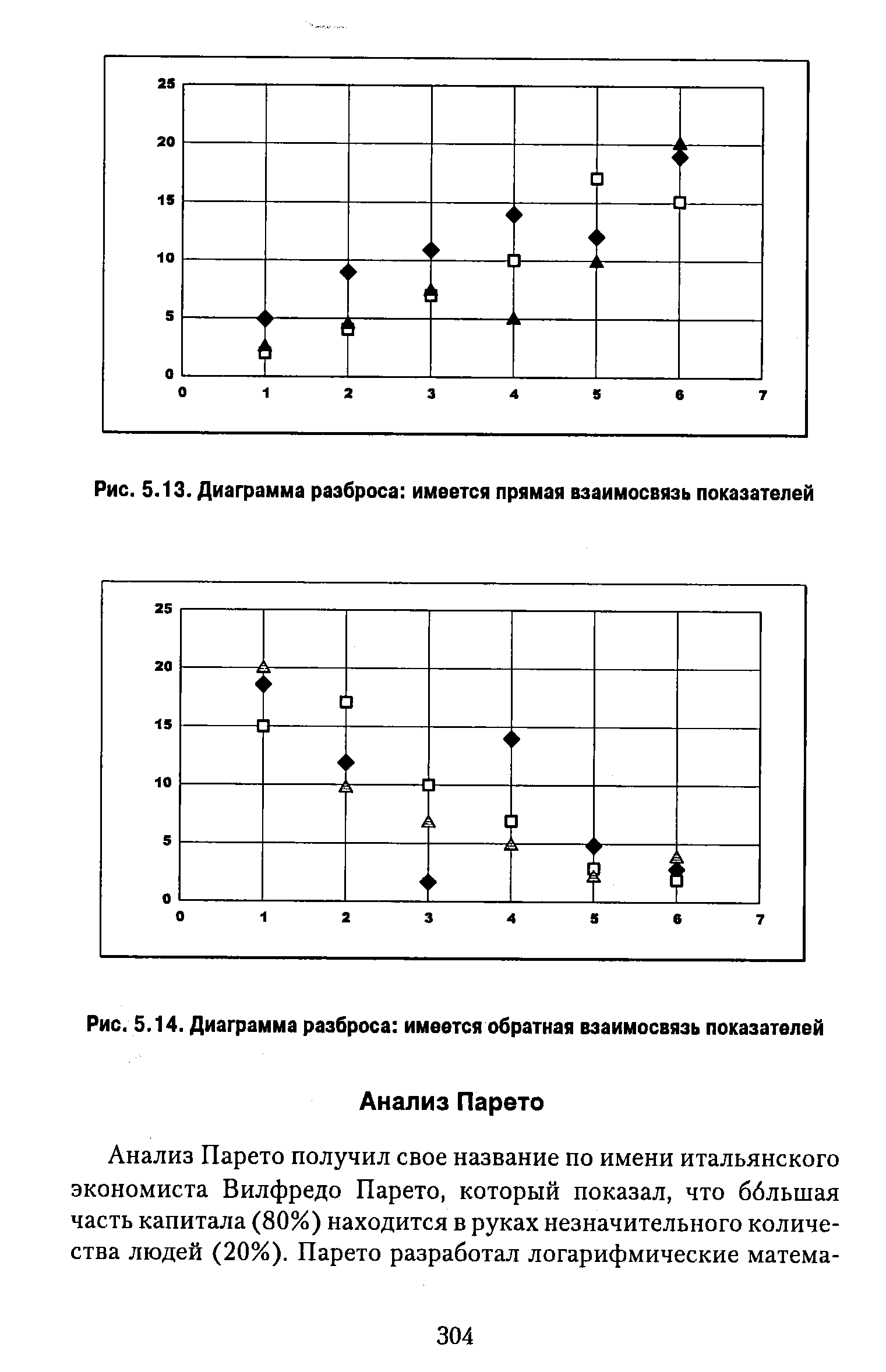

Стратификация является методической основой для других инструментов — таких, как анализ Парето или диаграммы разброса. Такое сочетание инструментов делает их более эффективными. На рис. 5.16 приведен пример анализа источника возникновения дефектов. Все дефекты (100%) классифицированы на 4 категории — по поставщикам, по операторам, по смене и по оборудованию.  [c.306]

Диаграммы разброса — это графики виды которых приведены на рис. 5.14—5.16. Диаграммы позволяют выявить корреляцию между двумя различными факторами.  [c.363]

Рис. 5.14. Диаграмма разброса при отсутствии взаимосвязи между показателями 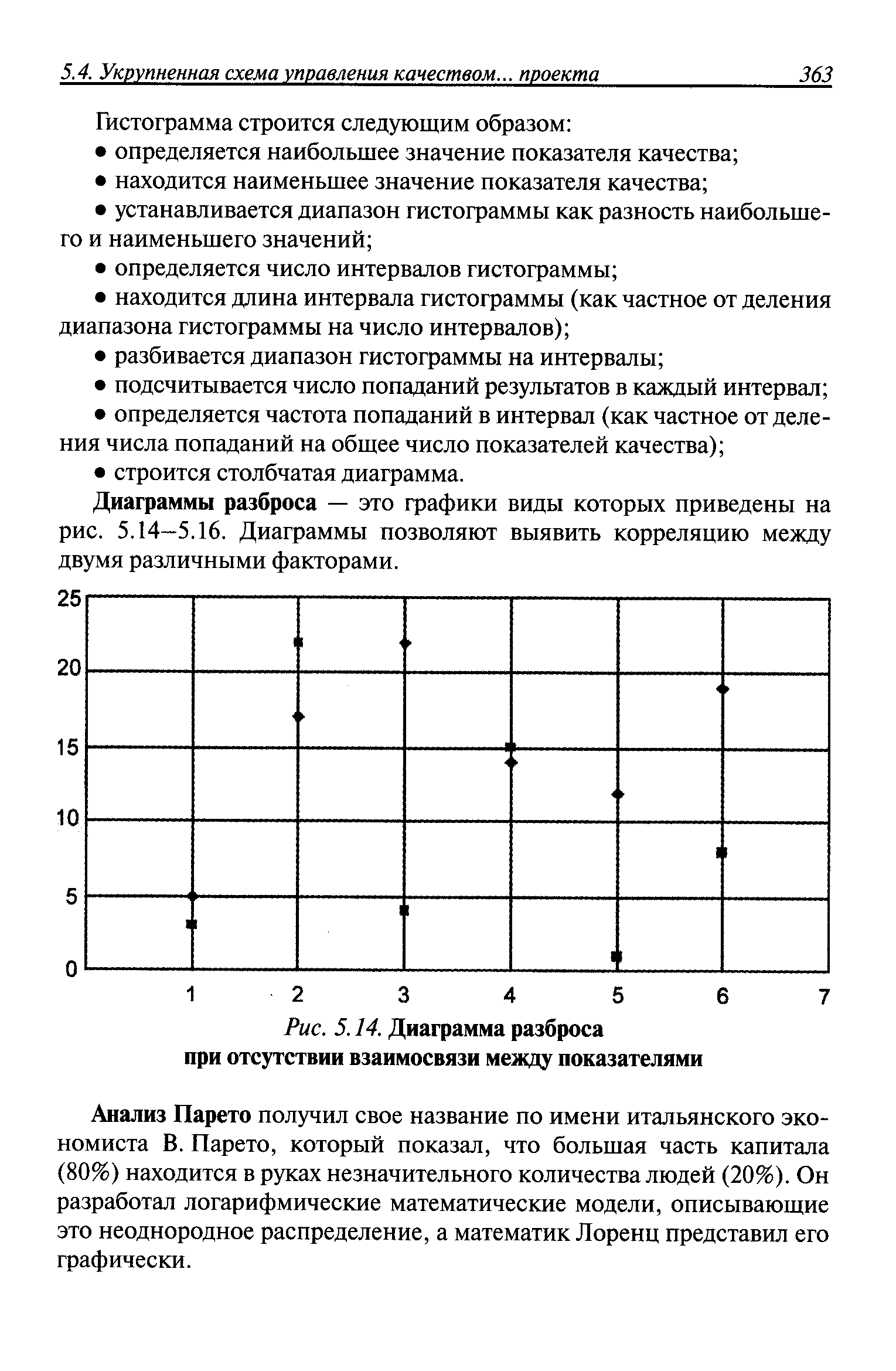Рис. 5.14. Диаграмма разброса при отсутствии <a href="/info/196664">взаимосвязи между</a> показателями
Рис. 5.15. Диаграмма разброса при прямой взаимосвязи показателей  [c.364]

Рис. 5.16. Диаграмма разброса при обратной взаимосвязи показателей  [c.364]

Диаграммы разброса. Они позволяют выявить корреляцию между двумя различными факторами. Диаграммы строятся следующим образом. По оси абсцисс откладываются значения фактора причины, например изменение телефонной плотности в квартирном секторе за ряд лет, а по оси ординат — значения фактора следствия, например количество междугородных телефонных разговоров с одного аппарата. Таким образом получается совокупность точек. Эту совокупность обводят сплошной линией. Если получается овал, то считается, что между исследуемыми факторами есть корреляция, если круг, то корреляция отсутствует.  [c.263]

B. Диаграммы разброса. Г. Диаграммы Парето.  [c.18]

Вы наверное заметили, что в методах, которые приводятся в учебнике РМВОК, диаграммы разброса не указаны. Учебник РМВОК не относит эти диаграммы к методам и приемам процесса контроля качества, однако на экзамене вы можете получить подобный вопрос.  [c.398]

В диаграмме разброса используются две переменные, одна из которых независимая и является входом, а вторая зависимая и является выходом. В диаграмме представлена зависимость между этими переменными в виде точек. Например, в виде подобной диаграммы вы можете сравнить возможности двух служащих для выполнения одного задания. Их опыт в выполнении подобных заданий в месяцах мы откладываем по оси X как независимую переменную, а оценку их работы как зависимую переменную — по оси Y. Образец подобной диаграммы представлен на рис. 10.3.  [c.399]

A. Статистическая выборка. Б. Диаграммы разброса.  [c.411]

B. Диаграмма производственного процесса. Г. Диаграмма разброса.  [c.412]

Г. В диаграмме разброса используются две переменные, зависимая и независимая, чтобы показать связь между двумя элементами в виде точек на графике.  [c.414]

B. Диаграмма причины и следствия. Г. Диаграмма разброса.  [c.482]

Вовлеченность в работу всех сотрудников базируется на овладении специальными знаниями в области качества путем обучения методам обеспечения качества и повышения квалификации персонала. Важным в этом процессе является овладение персоналом всеми инструментами контроля качества, которые обеспечивают необходимые статистические данные для их последующего анализа специалистами. Авторы TQM рекомендуют семь таких инструментов (контрольный листок возможных состояний и частоты их проявления, графическое представление статистического материала в виде гистограммы, диаграмма разброса между параметрами, диаграмма учета весомости причин — диаграмма Паре-то, причинно-следственная диаграмма Исикавы, контрольная карта хода процесса и метод стратификации).  [c.469]

В специальной литературе приводятся несколько вариантов набора инструментов качества. Например, в [7, 23] рассматривается семь инструментов качества метод расслоения информации по группам факторов, влияющих на качество процессов, графики, диаграммы Парето, причинно-следственные диаграммы (диаграмма Исикавы), гистограммы, диаграммы разброса, контрольные карты и контрольные листки. В этом же источнике приводятся семь дополнительных инструментов качества диаграммы сродства (сходства), диаграммы зависимостей, системные (древовидные) диаграммы, матричные диаграммы, сетевые графы, диаграммы планирования процессов, метод анализа матричных данных. В [23] приведены девять инструментов качества 1) построение схемы процесса 2) контрольный листок 3) мозговая атака 4) диаграмма Парето 5) причинно-следственная диаграмма (диаграмма Исикавы) 6) временной ряд 7) гистограмма 8) диаграмма рассеяния (корреляционное поле) 9) контрольная карта.  [c.470]