Показатель асимметрии (А) и его ошибка (та) рассчитываются по следующим формулам [c.143]
As называют коэффициентом асимметрии. Он может быть рассчитан как по сгруппированным, так и по несгруппированным данным. По данным табл. 5.6 показатель асимметрии составил [c.110]
Показатель Пирсона зависит от степени асимметричности в средней части ряда распределения, а показатель асимметрии, основанный на моменте третьего порядка, - от крайних значений признака. Таким образом, в нашем примере в средней части распределения асимметрия более значительна, что видно и по графику (рис. 5.1). Распределения с сильной правосторонней и левосторонней (положительной и отрицательной) асимметрией показаны на рис. 5.3. [c.110]
По значениям показателей асимметрии и эксцесса распределения можно судить о близости распределения к нормальному, что бывает существенно важно для оценки результатов корреляционного и регрессионного анализа, возможностей вероятностной оценки прогнозов (см. главы 7,8,9). Распределение можно считать нормальным, а точнее говоря - не отвергать гипотезу о сходстве фактичес- [c.112]
В-пятых, распределение признаков, включаемых в модель, должно быть близким к нормальному. Существуют различные статистические методы проверки нормальности распределения (самый простой — через показатели асимметрии и эксцесса). Выполнение этого требования в экономических исследованиях нередко сопряжено с существенными трудностями и не всегда возможно. [c.83]
Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт степени тесноты связи, не вскрывая ее причин. Кроме того, не существует общеупотребительного критерия проверки нормальности совместного распределения анализируемых переменных, поэтому обычно ограничиваются проверкой нормальности частных одномерных распределений. В условиях малых выборок подобная проверка может быть осуществлена с помощью показателей асимметрии и эксцесса, рассчитываемых через показатели центральных моментов третьего и четвертого порядков и среднее квадратическое отклонение. [c.119]
На рис. 1.18 приведены три типичных распределения. Когда данные симметричны, тогда значения арифметической средней, медианы и моды совпадают. Напротив, когда распределение положительно асимметрично, т. е. шлейф длиннее в правой части распределения, тогда арифметическая средняя является наибольшим значением, а мода — наименьшим. То же самое относится и к отрицательно асимметричному распределению, когда шлейф длиннее в левой части шкалы. Все это подводит к способу измерения формы (или асимметрии) данных. Нижеприведенные значения дают два сходных показателя асимметрии [c.47]
Показатель асимметрии 0,50263 Показатель эксцесса —0,29715 —01 [c.222]
Показатель асимметрии 0,52392 —01 Показатель эксцесса 1,2619 [c.224]
Показатель асимметрии 0,13040/ —01 Показатель эксцесса —0,15626 [c.225]
Число единиц в выборке, N Величина интервала, Н Показатель асимметрии ряда, гл Показатель эксцесса, Ех Дисперсия, а Среднее значение, X Критерий согласия, К [c.81]
Мы уже видели в Главе 13 связь между показателем Херста Н и спектральным показателем PS. (Теперь мы будем именовать спектральный показатель как PS, чтобы отличить его от показателя асимметрии Р). Уравнение (14.10) позволяет нам выразить отношение с fa [c.205]
Однако показателем асимметрии, который наиболее пригоден для применения в случае сгруппированных данных, является коэффициент асимметрии, основанный на расчете моментов распределения. Он определяется с помощью центрального момента третьего порядка и деления его на куб среднего квадратического отклонения, что можно представить следующей формулой [c.93]
В то время как показатели асимметрии характеризуют симметричность распределения частот, показатели эксцесса описывают [c.94]
Для симметричных распределений погрешностей медиана совпадает с их математическим ожиданием. Это обстоятельство служит иногда для проверки симметричности распределений. Однако более часто для проверки симметричности распределений используют показатель асимметрии (или скошенности") 5К теоретическое значение которого определяется формулой [c.63]
Следующее требование к исходной информации — подчинение ее закону нормального распределения. Для количественной оценки степени отклонения информации от нормального распределения служат отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке. [c.40]
Г3 = — - — показатель асимметрии, если Г3 (J, то распределение величины [c.2]
| Рис. 5.3. Асимметрия распределения Показатель эксцесса рассчитывается по формуле | 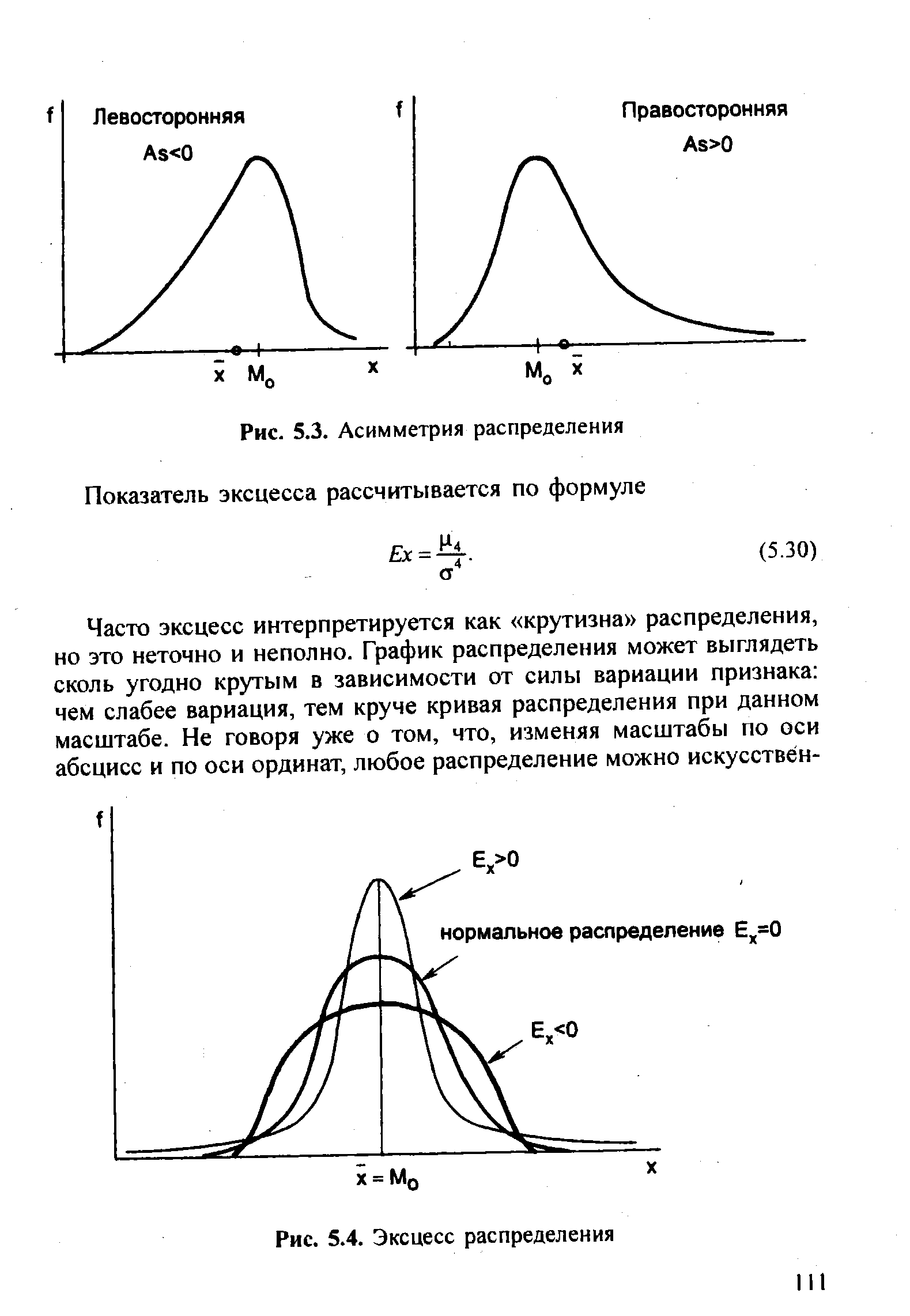 |
Т Определение. Асимметрия — это показатель формы (степени симметрии) распределения. А [c.48]
Показатель Среднее СКО Вариация Асимметрия Эксцесс [c.103]
Показатели формы распределения - коэффициент асимметрии. [c.21]
При изучении формы распределения случайной величины важно выяснить, симметрична ли относительно центра распределения кривая плотности вероятности. Показателем степени несимметричности этой кривой является безразмерная величина, называемая коэффициентом асимметрии. Коэффициент асимметрии обозначается как у или As. Рассмотрим на качественном уровне понятие асимметрии. [c.21]
В случае, если кривая плотности вероятности имеет крутой левый и пологий правый спад, говорят, что распределение имеет положительную асимметрию. В этом случае координаты показателей центра распределения располагаются на оси абсцисс, как правило, следующим образом мода < медиана < математическое ожидание. [c.21]
Если кривая плотности вероятности имеет пологий левый и крутой правый спад, распределение имеет отрицательную асимметрию. В этом случае для показателей центра распределения имеем математическое ожидание < медиана < мода. [c.21]
Если в качестве показателя центра распределения выбрано математическое ожидание, то коэффициент асимметрии рассчитывают, используя третий центральный момент распределения. [c.22]
Математическое ожидание Дисперсия Среднее квадрати-ческое отклонение 0,89069 -01 0,3SOf>OE-03 0.19509Я-01 Показатель асимметрии Показатель эксцесса Коэффициент вариации 0,22514 -0,82376 21,903 [c.221]
Распределение частот количественного признака. Гистограмма и кумулята. Функции распределения вероятностей и плотности распределения вероятности. Типы распределения. Средние величины. Средние степенные квадратические, арифметические, геометрические, гармонические. Мажорантность средних степенных. Средние хронологические. Средние относительные величины. Мода, медиана, квантили. Моменты. Дисперсия, показатель асимметрии, эксцесс, куртозис. [c.49]
В нормальном распределении показатель эксцесса Е = 0. Если Е > О, то данные густо сгруппированы около средней, образуя островершинность. Если Е < 0, то кривая распределения будет плосковершинной. Однако, когда отношения А/та и Е/те меньше 3, то асимметрия и эксцесс [c.143]
Идентификация случайных параметров модели осуществляется с использованием стандартных программ, входящих в состав математического обеспечения современных универсальных ЭВМ. Так, например, в математическом обеспечении ЕС ЭВМ имеется программа, осуществляющая расчет эмпирического распределения, ее сравнение с множеством теоретических законов распределения (нормальное, равномерное, Вейбулла, гамма, экспоненциальное и т. п.), проверку гипотезы о соответствии выбранного закона распределения эмпирическим данным. Проверка гипотезы осуществляется по критериям Пирсона, Романовского, Колмогорова—Смирнова. Программа обеспечивает расчет основных параметров выбранного закона распределения — математического ожидания, дисперсии, среднеквадратического отклонения, показателей эксцесса и асимметрии и коэффициента вариации. [c.96]
Вклад переменной RETLAG (доход за время с f-2 до t- 1) невелик, и этого следовало ожидать, поскольку изменения зависимой переменной описываются если не случайным блужданием, то, во всяком случае, мартингальным процессом (см. [177]). Существенная роль переменной LEVELLAG (предыдущий показатель индекса) подтверждает гипотезу о том, что уровень индекса является важным лидирующим показателем для ожидаемого дохода. То обстоятельство, что регрессия не квалифицирует эту переменную как значимую, может говорить о том, что в механизме влияния уровня индекса на доход имеется какая-то асимметрия, возможно, связанная с нелинейной обратной связью. Это наблюдение интуитивно придает дополнительный вес гипотезе встречных инвестиций, которую высказал Чан [62] и ряд других авторов. Поведение рынка, для которого характерны возвращения к средним значениям, если оно, действительно, имеет место, неявно опровергает гипотезу эффективного рынка. [c.153]
В конце концов цель процедур отбора — производить информацию, которую не позволяет выявить или плохо выявляет система цен3. Так, на рынке труда выбор одного из двух кандидатов, похожих между собой, если пользоваться языком рыночных показателей, основывается на отборе информации о предпочтениях индивидов и, следовательно, их способности интегрироваться в организацию. Но это означает также, что организация будет тем эффективнее, чем удачнее будет выбор ее участников. Процедуры обучения играют аналогичную роль4. Нобелевский лауреат Кеннет Эрроу (Arrow К. J.) показал, что производитель зависит от обучения, т. е. от способности организации передать информацию и внедрить дисциплину. Однако обучение связано не только с намерением уменьшить асимметрию информации, например между учителем и учеником лицом к лицу с действительностью (связанной с неблагоприятным отбором). [c.376]
Эта асимметрия информации имеет важные следствия для маркетинга, и прежде всего для брендинга. Название марки часто воспринимается потребителями как основной показатель качества продукта (M arthy and Shapiro, 1983). Поскольку потребители должны доплачивать за качественную марку (Nagle, 1984), специалисты по сбыту, способные создавать и поддерживать имидж высококачественной торговой марки, могут получить дополнительные прибыли. [c.110]
