Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице [c.32]
Если интеграл (12.2) при b — +00 имеет бесконечный предел или вовсе не имеет предела, то говорят, что несобственный интеграл (12.3) расходится. Если интеграл (12.2) при b — +00 имеет конечный предел, то говорят, что несобственный интеграл (12.3) сходится. [c.261]
Геометрический смысл несобственного интеграла (12.3) для неотрицательной на [а, +оо) функции /(ж) состоит в том, что он представляет собой площадь криволинейной фигуры, ограниченной данной линией у = /(ж), осью Ох и вертикалью х = а. [c.262]
Значит, искомый несобственный интеграл расходится. Геометрически это означает, что площадь области под гиперболой у = — [c.263]
Сходимость и расходимость несобственного интеграла f / (x) dx [c.263]
Определение 4. Пусть функция /(ж) непрерывна при а < х 6 и имеет точку разрыва при х — а. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой [c.266]
Аналогично определяется несобственный интеграл, когда /(ж) имеет разрыв только на конце х = b промежутка [а, 6). [c.266]
V Пример 5. Найти несобственный интеграл — dx. [c.266]
Искомый несобственный интеграл расходится. Геометрически это означает, что соответствующая криволинейная трапеция ( бесконечный шпиль ) имеет бесконечную площадь (рис. 12.17). А [c.266]
| Рис. 12.17. Геометрический смысл несобственного интеграла | 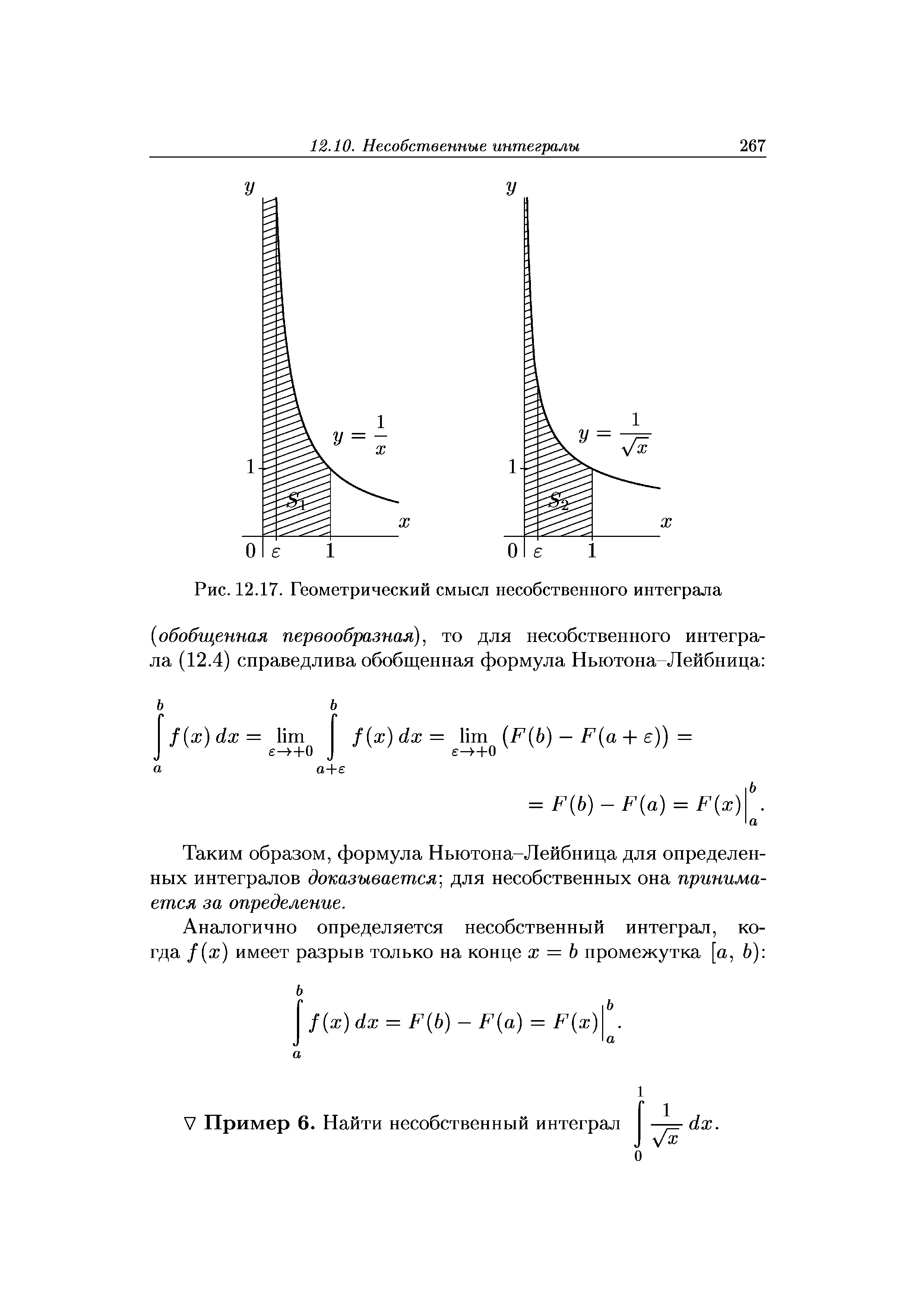 |
Вычисляем каждый несобственный интеграл в отдельности [c.43]
Несобственный интеграл. Сходимость и расходимость несобственных интегралов. Признак сравнения для несобственных интегралов. [c.15]
Исследование сходимости несобственного интеграла x"dx в зависимости от п. [c.15]
Если использовать рациональные преобразования, предложенные в [I], то несобственный интеграл для слабосингулярного ядра Ржаницына-Колтунова [c.208]
Можно обобщить данное выше определение и на случай бесконечных (по времени), точнее, нефинитных потоков, если понимать интеграл в (1 1.7) как несобственный. [c.421]
Поскольку поток нефинитный (бесконечный), то интеграл (11.7) будет несобственным [c.422]
При рассмотрении определенного интеграла как предела интегральных сумм предполагалось, что подынтегральная функция ограничена m конечном отрезке интегрирования. Данное ранее определение оп-редечетшого интеграла не имеет смысла npit невыполнении хотя бы одного из этих условий. Нельзя разбить бесконечный интервал на конечное число отрезков конечной дчины, при неограниченной функции интегральная сумма не имеет предела. Тем не менее, возможно обобщить понятие определенного интеграла и на эти случаи, с чем и связано понятие несобственною интеграла. [c.144]
| Рис. 7,5 Если этот предел я онечен, то несобственный интеграл | 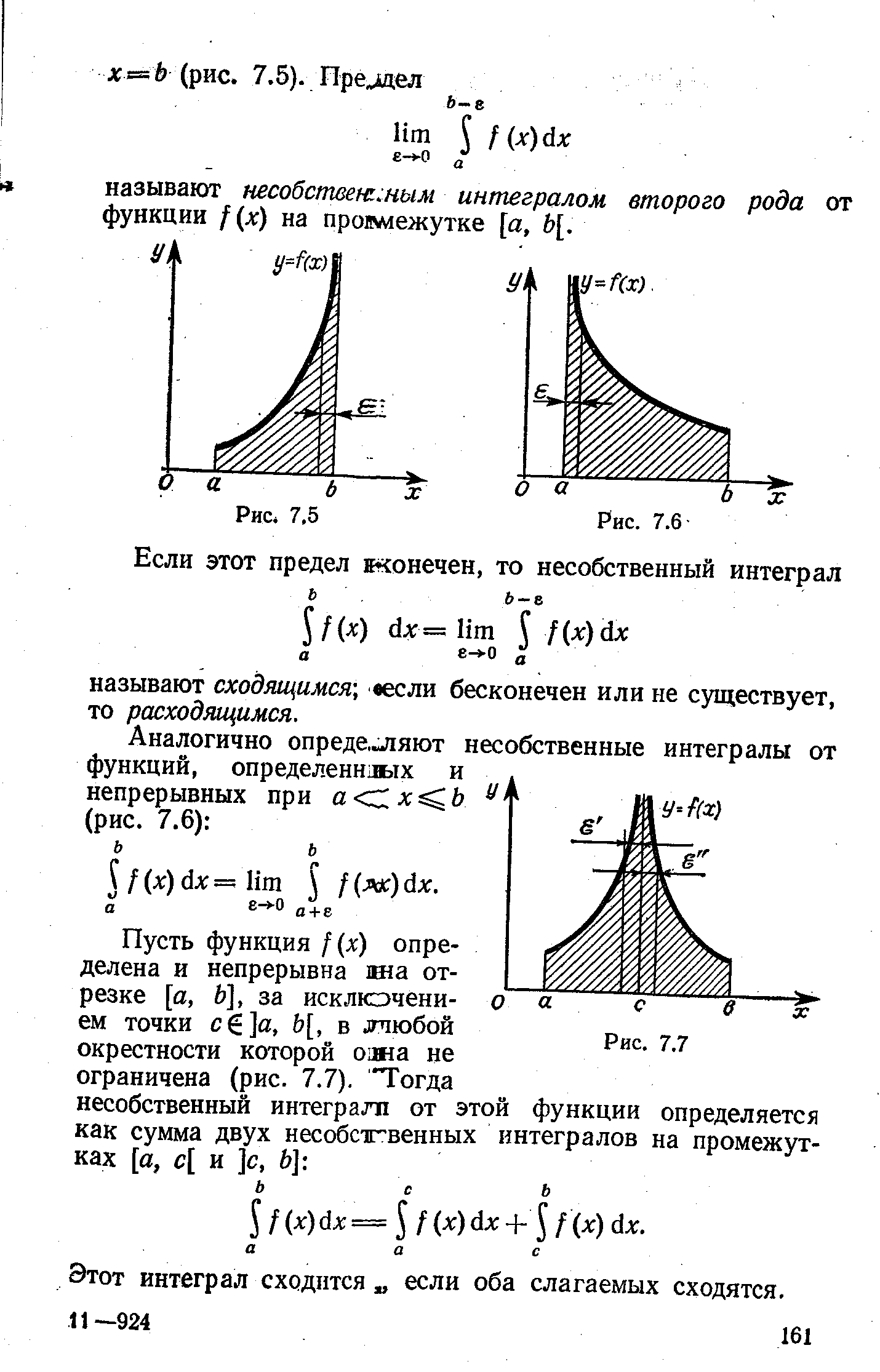 |
