Определенный интеграл

Операция вычисления определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования выполняется по стандартной программе, заложенной в память машины. В этой связи задача сводится лишь к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.  [c.134]


Последующее вычисление определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования выполняется при помощи ЭВМ по стандартной программе, в которой используется формула Симпсона, или вручную в соответствии с общими правилами интегрирования.  [c.138]

Отношение площади между линией равномерного распределения и линией фактического распределения ко всей площади под линией равномерного распределения, принятой за единицу, также является одним из показателей неравномерности распределения. Без вычисления ясно, что площадь под линией равномерного распределения равна половине площади квадрата, т. е. 0,5 в принятом масштабе, где и dH и dx изменяются от 0 до +1. Если точное выражение функции dx через dH неизвестно вычислить площадь под фактической кривой нельзя, а измерить на диаграмме тоже сложно. Зато мы можем легко вычислить площадь под приближенной функцией d x = (d H)3, которая выразится как определенный интеграл этой функции, если d H обозначить X  [c.451]


Пособие удовлетворяет требованиям новых государственных образовательных стандартов к минимуму содержания и уровню подготовки в области математики для социально-экономических направлений и специальностей и написано в соответствии с примерной программой дисциплины Математика , одобренной Научно-методическим советом по математике Министерства образования Российской Федерации. Пособие включает следующие девять разделов программы Введение в математический анализ , Основы математической логики , Дифференциальное исчисление функций одной переменной , Применение дифференциального исчисления для исследования функций и построения их графиков , Неопределенный интеграл , Определенный интеграл , Функции нескольких переменных , Обыкновенные дифференциальные уравнения , Системы обыкновенных дифференциальных уравнений . Кроме обязательного материала автор счел необходимым включить в пособие главу, посвященную разностным уравнениям, широко используемым в экономической теории.  [c.9]

Надо хорошо представлять все возможности и недостатки пакета символьных вычислений. При недостаточном ознакомлении с пакетом и методами решения пользователь может сделать неверный вывод. Поэтому в пособии показано как различия в методах влияют на скорость сходимости и круг решаемых задач (см. п. 12.8, в котором рассмотрены различия трех приближенных формул вычисления определенного интеграла).  [c.15]

Глава 12 Определенный интеграл  [c.220]

Понятие определенного интеграла  [c.223]

Понятие определенного интеграла 225  [c.225]

Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия. Неопределенный интеграл представляет функцию (а точнее семейство функций), а определенный интеграл — это число.  [c.226]


Из определения следует, что величина определенного интеграла не зависит от обозначения переменной интегрирования, т. е.  [c.226]

Понятие определенного интеграла распространяют и на случай а = 6 интеграл с равными пределами считается равным нулю  [c.227]

Если а < b и /(ж) меняет знак на отрезке [а, 6], то определенный интеграл равен алгебраической сумме площадей соответствующих криволинейных трапеций (рис. 12.3)  [c.228]

Определение интегральной суммы позволяет использовать понятие определенного интеграла в социально-экономической сфере. Его применение основано на том, что любой меняющийся социально-экономический процесс может быть интерпретирован как скачкообразный, скачки которого близки к нулю.  [c.229]

Учитывая определение определенного интеграла, окончательно получаем  [c.230]

Свойства определенного интеграла 231  [c.231]

Рассмотрим сначала свойства определенного интеграла, которые имеют аналоги в случае интеграла неопределенного.  [c.231]

По определению определенного интеграла первый из пределов  [c.232]

Перейдем теперь к свойствам определенного интеграла, которые не имеют аналогов в случае неопределенного интеграла.  [c.233]

При а < с < Ъ это равенство имеет простой геометрический смысл (см. рис. 12.4, а). Согласно геометрическому смыслу определенного интеграла  [c.233]

Рис. 12.4. Третье свойство определенного интеграла 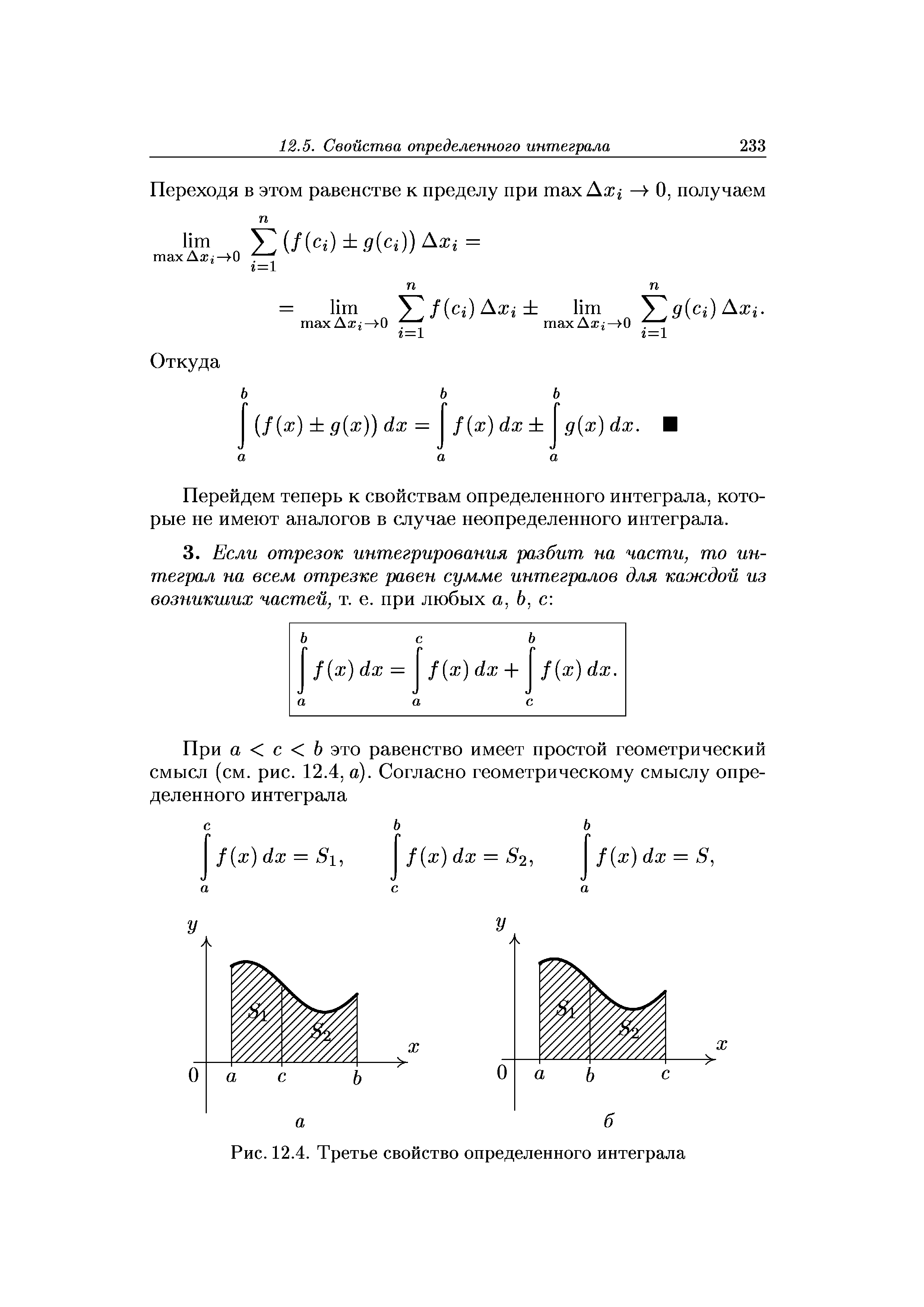Рис. 12.4. Третье свойство определенного интеграла
Действительно, в качестве такой первообразной всегда можно предъявить определенный интеграл с переменным верхним пределом Ф(ж), поскольку Ф (ж) = /(ж).  [c.238]

Теорема (формула Ньютона-Лейбница). Пусть функция у — /(ж) непрерывна на отрезке [а, 6] и F(x) — произвольная первообразная для /(ж) на [а, Ь]. Тогда определенный интеграл от функции /(ж) на [а, 6] равен разности значений первообразной F(x] для верхнего и нижнего предела интегрирования, т. е.  [c.238]

Формула Ньютона-Лейбница сводит вычисление определенного интеграла к отысканию неопределенного интеграла. Чтобы  [c.239]

Доказанную формулу называют формулой замены переменной под знаком определенного интеграла. При использовании этой формулы определенного интеграла  [c.241]

КОШЙ ( au hy) Огюстен Луи (1789-1857), французский математик, член Парижской Академии наук. Работал инженером в Шербуре, преподавал в Политехнической школе, Колеж де Франс и в Парижском университете (отказывался от должности в университете до тех пор, пока не была отменена присяга в лояльности правительству). Оставил свой след во многих областях математики. Его курсы анализа, основанные на систематическом использовании понятия предела, послужили образцом для большинства курсов позднейшего времени. В них он дал определение понятия непрерывности функции, четкое определение сходящихся рядов, определение интеграла как предела суммы и др.  [c.59]

Экономико-математический словарь Изд.5 (2003) -- [ c.125 ]