Если задан односторонний допуск, то вероятность его соблюдения выражает интеграл [c.152]
Сила трения, создаваемая в результате контакта ленты со шкивом вычисляем с помощью интеграла [c.95]
Пользуясь выражениями (4) и (5) находим интеграл [c.95]
Интегральный метод дает наиболее общий подход к решению задач факторного анализа по разложению общего прироста показателя по факторным приращениям. В основе интегрального метода лежит интеграл Эйлера — Лагранжа, устанавливающий связь между приращением функции и приращением факторных признаков. Для функции z = (x, у) имеем следующие формулы расчета факторных влияний. [c.275]
Учитывая эти две формулы, интеграл по отрезку I можно записать следующим образом [c.131]
Операция вычисления определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования выполняется по стандартной программе, заложенной в память машины. В этой связи задача сводится лишь к построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы. [c.134]
Формирование рабочих формул интегрального метода для кратных моделей. Подынтегральные выражения элементов структуры факторной системы для- кратных моделей строятся путем ввода под знак интеграла исходного значения, полученного на пересечении строк в зависимости от вида модели и элементов структуры факторной системы с последующей расшифровкой значений, приведенных справа и в низу матрицы исходных значений. [c.136]
Последующее вычисление определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования выполняется при помощи ЭВМ по стандартной программе, в которой используется формула Симпсона, или вручную в соответствии с общими правилами интегрирования. [c.138]
Тогда интеграл по траектории преобразуется в обычный интеграл, вычисляемый на отрезке [О, 1] по формуле [c.11]
| Рис. 1.3. График изменения фактора по ломаной линии Примечание. Рассмотрите интеграл |  |
| Таблица 6.1 Значения интеграла вероятностей — функции Лапласа | 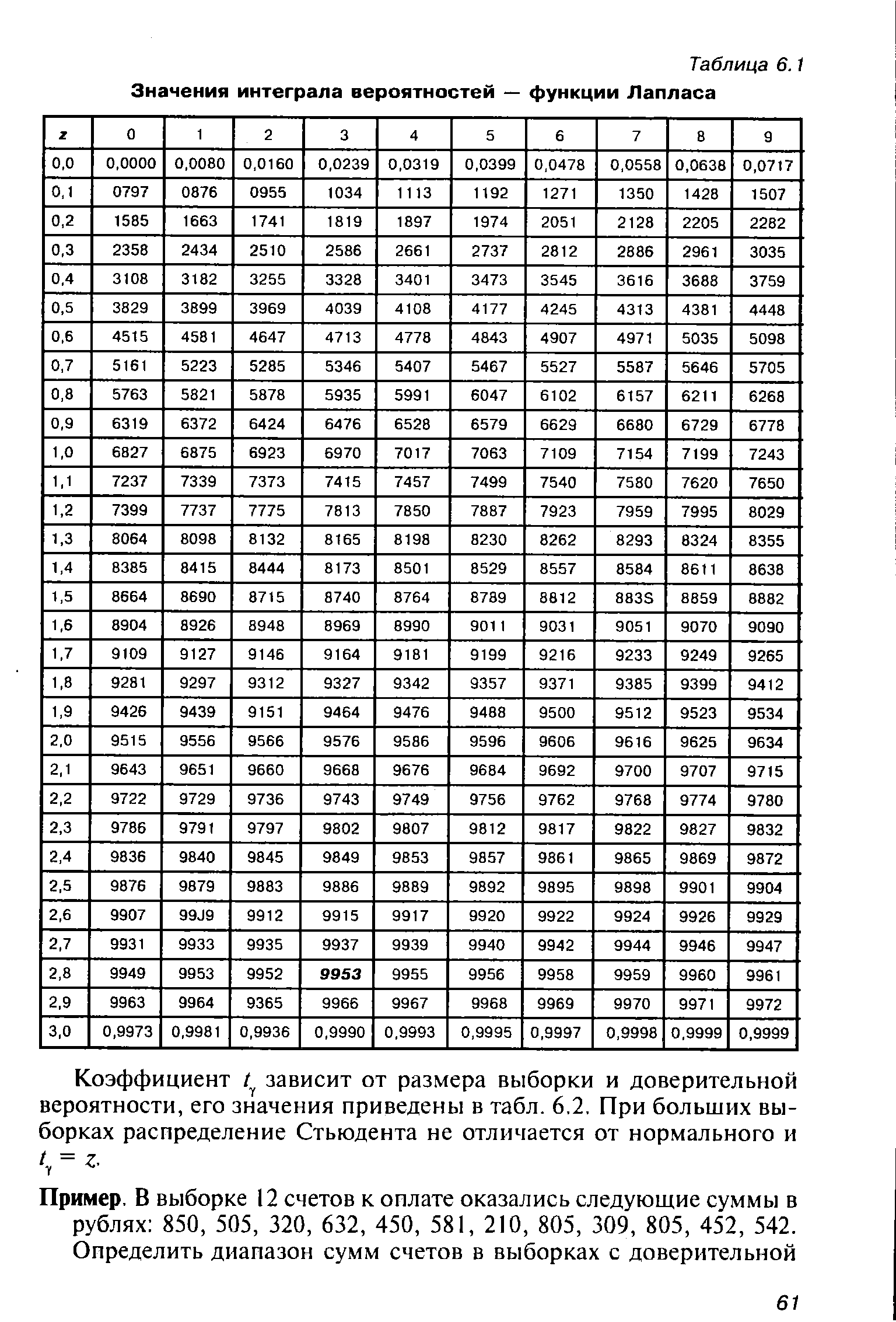 |
На пересечении строк и граф таблицы находится значение вероятности F(t), соответствующее данному значению /. Для краткости записи в таблице приводятся только десятичные знаки вероятности, следовательно, к табличному значению F(t) надо приписывать ноль целых. Например, чтобы определить, какая вероятность соответствует /= 1,96, надо взять строку 1,9 и графу 6 и на их пересечении прочитать значение вероятности, добавив перед первым знаком ноль целых. Если / = 1,96, то F(f)= 0,9500. По мере увеличения t (уже при / = 3) значение интеграла вероятностей приближается к единице. Чем шире пределы t, тем большая площадь под кривой охватывается ординатами, восстановленными из соответствующих значений /. Поскольку вероятность — это отношение части площади под кривой, заключенной между ординатами, ко всей площади, соответственно возрастает и вероятность. [c.168]
Нормированное отклонение / может быть установлено по таблице Значение интеграла вероятностей . Для этого необходимо принять определенный уровень вероятности суждения о точности данной выборки. [c.168]
Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности. Но уже при п < 100 получается несоответствие между табличными данными и вероятностью предела при п < 30 погрешность становится значительной. Несоответствие вызывается главным образом характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, так как распределение отклонений выборочного показателя от генеральной характеристики при большой выборке всегда оказывается нормальным. [c.190]
Если бы мы использовали для расчета доверительных границ генерального параметра таблицу интеграла вероятностей, то / было бы равно 1,96 и Ар - 0,31, т. е. доверительный интервал был бы несколько уже. [c.192]
Первая задача чаще всего решается при неизвестной генеральной дисперсии. Испытуемая гипотеза Н0 ц = ца, альтернативная гипотеза Н ц Ф ц0. Испытание гипотезы проводят с помощью /- критерия. При большом числе наблюдений критическое значение критерия определяется по таблице интеграла вероятностей, при малом - по таблице распределения Стьюдента с заданным уровнем значимости и числом степеней свободы, п - 1. [c.208]
Отношение площади между линией равномерного распределения и линией фактического распределения ко всей площади под линией равномерного распределения, принятой за единицу, также является одним из показателей неравномерности распределения. Без вычисления ясно, что площадь под линией равномерного распределения равна половине площади квадрата, т. е. 0,5 в принятом масштабе, где и dH и dx изменяются от 0 до +1. Если точное выражение функции dx через dH неизвестно вычислить площадь под фактической кривой нельзя, а измерить на диаграмме тоже сложно. Зато мы можем легко вычислить площадь под приближенной функцией d x = (d H)3, которая выразится как определенный интеграл этой функции, если d H обозначить X [c.451]
Из формулы баланса видно, что первый двойной интеграл в левой части формулы отражает стоимость актива, второй — величину текущих расходов в правой части двойной интеграл отражает объем пассива, а последний интеграл характеризует величину полученных фирмой доходов. [c.420]
Значения этого интеграла для различных значений коэффициента доверия / вычислены и приводятся в специальных математических таблицах. В частности, при [c.132]
При выездной налоговой проверке АО Интеграл установлено, что организацией при исчислении налогооблагаемой прибыли на себестоимость реализованной продукции (работ, услуг) отнесены затраты на ремонт здания, произведенный хозяйственным способом. [c.223]
В результате выездной налоговой проверки налогооблагаемая прибыль АО Интеграл за соответствующий период увеличена на сумму неправомерно отнесенных на себестоимость продукции (работ, услуг) затрат на капитальный ремонт здания. Доначислена сумма налога на прибыль и начислены пени. Организация привлечена к ответственности за совершение налогового правонарушения, предусмотренного п. 1 ст. 122 НК РФ, в виде штрафа в размере 20% суммы доначисленного налога. [c.224]
Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице [c.32]
Идентифицируемость модели 22 Интеграл вероятностей Лапласа 35 Интервальная оценка параметра 44 [c.300]
В качестве траектории L, по которой берется интеграл, чаще всего берется прямая, т.е. считается, что факторы изменяются линейно. Для двухфакторной модели [c.67]
Пользуясь готовыми таблицами значения интеграла вероятности, отыскиваем значение Ф (0,83) Р = Ф (0,83) =0,797. [c.143]
Таким образом, нет очевидных доказательств, что у специализированной компании уровень вертикальной интегра-выше, чем у [c.124]
Совершенствование товара Горизонтальная интегра- Конгломератная диверси- [c.582]
Тем не менее существует опасность, что эти интегра-тивные способности могут превратить Японию в этакого мастера на все руки , что помешает созданию новой большой оригинальной технологии. Данную проблему следует учитывать при определении перспективных направлений развития современной техники. [c.57]
Формы, структура и содержание договоров на консультационные услуги. Принципы организации консультант-клиентских отношений. Характеристика экспертного, диагностического, обучающего и интегра-тивного консультирования, организация выполнения консультационных работ. Содержание завершающего консультационного отчета. [c.308]
Если использовать рациональные преобразования, предложенные в [I], то несобственный интеграл для слабосингулярного ядра Ржаницына-Колтунова [c.208]
В совокупностях достаточно большого объема вместо таблицы распределения Стъюдента можно пользоваться таблицей интеграла вероятностей. [c.324]
Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить / и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < п < 100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц). [c.190]
Расчет риска продавца. Как уже сказано выше, риск продавца заключается в том, что отпускная цена на товар окажется ниже закупочной. Для расчета этого риска необходимо определить зависимость вероятности от отпускной цены на товар, для чего oieflyef вычислить интеграл (17.6). [c.456]
Политика контроля нефтедобычи, введенная в действие в США, состояла из серии штатных и федеральных законодательных актов, рекомендаций комиссий экономистов, интегри]юванных нефтяных компаний и Бюро недр министерства внутренних дел. Взятые в совокупности, эти акты представляли превосходный образец монополистического контроля над добычей нефти, распределением ее между компаниями по переработке нефти и, в конечном счёте, - продажей нефтепродуктов по цене, навязываемой потребителю. Политика государства, таким образом, способствовала формированию олигополистического рынка. [c.43]
В качестве методологической основы используются методы полумарковских процессов и теории операционного исчисления. Данные методы позволяют свести решение, систем интегро-дифференциальных уравнений, описывающих эксплуатацию объектов связи, к решению систем алгебраических уравнений с последующим определением оригиналов полученных выражений для основных показателей надежности при помощи известных методов обращения. В случае, когда нахождение оригинала в явном виде затруднено, применяется усовершенствованный алгоритм численного обращения двумерного преобразователя Лапласа, в котором для оценки оригинала используются полиномы Лагерра. Получено дальнейшее развитие подходов к формализации процесса эксплуатации технических объектов средств связи в виде аналитических выражений для основных показателей надежности, [c.167]
