Свойства определенного интеграла [c.231]
Рассмотрим сначала свойства определенного интеграла, которые имеют аналоги в случае интеграла неопределенного. [c.231]
Перейдем теперь к свойствам определенного интеграла, которые не имеют аналогов в случае неопределенного интеграла. [c.233]
| Рис. 12.4. Третье свойство определенного интеграла | 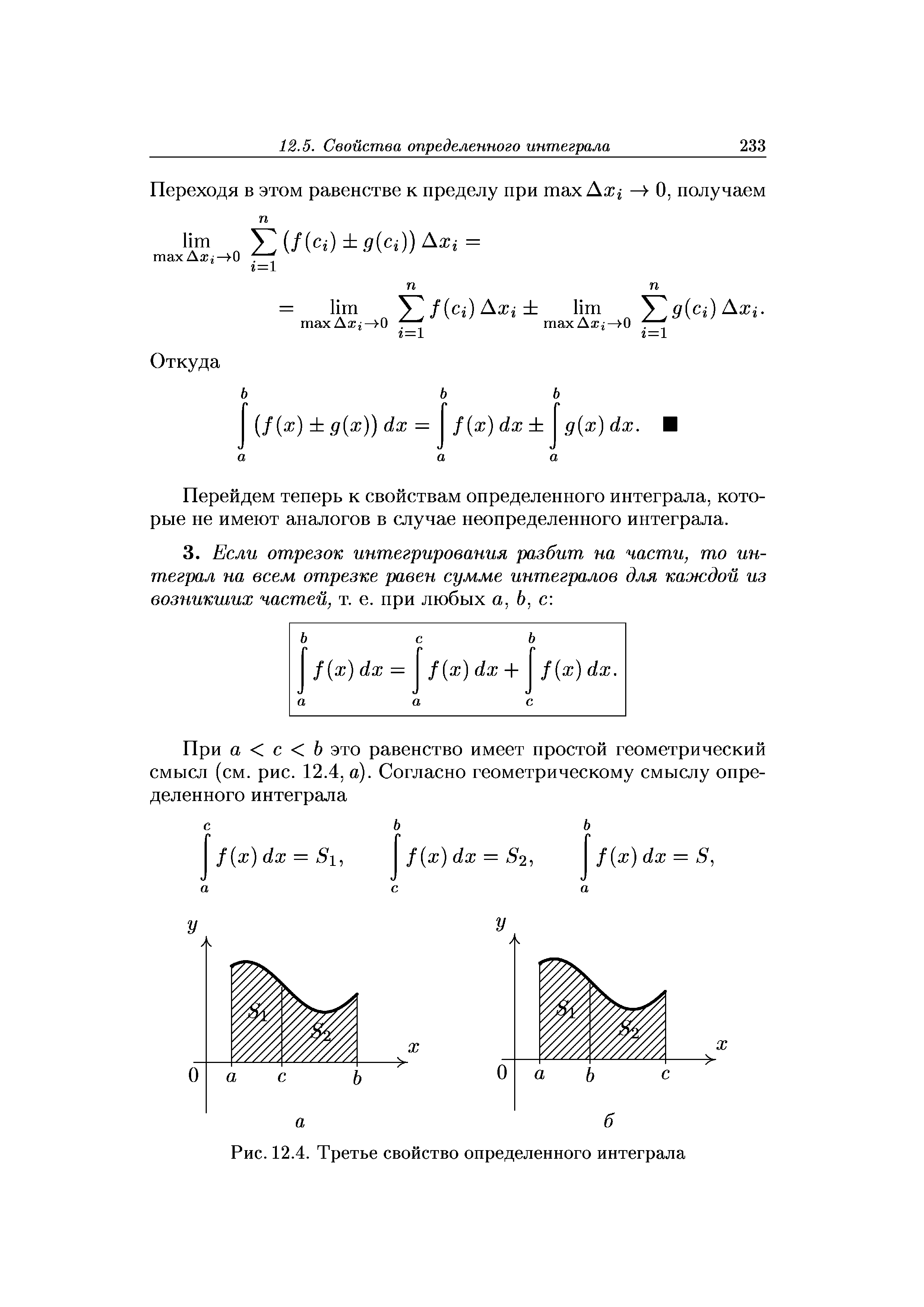 |
Основные свойства определенного интеграла. . . . 136 [c.6]
Основные свойства неопределенного интеграла. Пусть функция Р(х) является первообразной для функции Дх) на некотором промежутке X, т.е. F(x) =Л )- Тогда по определению f(x)dx = F(x) + С. Непосредственно из равенств (1) и (5) следуют свойства [c.57]
Использование предельных теорем. В некоторых случаях для имитации определенных законов распределения используют предельные теоремы теории вероятностей. Так, например, для получения нормального закона распределения используется свойство сходимости независимых величин к нормальному распределению. Метод обратной функции в этом случае оказывается неэффективным, так как получаемый при этом интеграл [c.206]
Замечание 1. Подчеркнем, что при определении таких интегралов от элементарных функций вовсе нет необходимости предполагать, что В = (Bt)t o - броуновское движение. В качестве процесса, по которому производится интегрирование, может выступать любой процесс. Однако специфика рассматриваемого сейчас броуновского движения становится существенной, если стремиться к тому, чтобы определить "стохастический интеграл" с простыми свойствами для более широкого запаса функций / — f(t,w), а не только для элементарных и их линейных комбинаций -простых функций. [c.308]
Предостережем читателя от автоматического переноса этого свойства на случай общих целочисленных случайных мер, например, мер скачков случайных процессов с непрерывным временем может случиться, что интеграл w (ц — v) определен, в то время как w // и w v равны +оо и, следовательно, их разность не имеет смысла см., подробнее, [250 гл. Ш].) [c.98]
Напомним еще раз, что в случае (скалярных) семимартингалов стохастический интеграл определен для всех локально ограниченных предсказуемых функций ( 5а, гл. III). При этом оказывается важным, в том числе и для расчетов в финансовой математике, то свойство стохастических интегралов по локальным мартингалам, что для таких функций эти интегралы являются также локальными мартингалами. [c.308]
Предположим, что Р - мартингальная мера, эквивалентная мере Р. Как говорилось в замечании 1 в 1а, свойство интегрируемости тг по X инвариантно относительно замены меры Р на ей эквивалентную меру Р. Тем самым, если тг Пэ (X), то векторный стохастический интеграл в (3) определен и по мере Р. [c.320]
Как следует из изложения в 1а, стохастический интеграл в (17) определен, если 7 L(S). В рассматриваемой сейчас модели (5) естественно условия интегрируемости 7 no S выражать непосредственно в терминах свойств процессов (jut)t T и (ot)t
Стандартным приемом локализации данное определение стохастического интеграла для тг L2 (М) распространяется затем и на предсказуемые процессы тг Lio (M), т.е. на те процессы, для которых выполнено свойство (14) с q — 2. [c.303]
Смотреть страницы где упоминается термин Свойства определенного интеграла
: [c.511]Смотреть главы в:
Математика для социологов и экономистов Учебное пособие -> Свойства определенного интеграла
