| Рис. 12.3. Геометрический смысл интеграла | 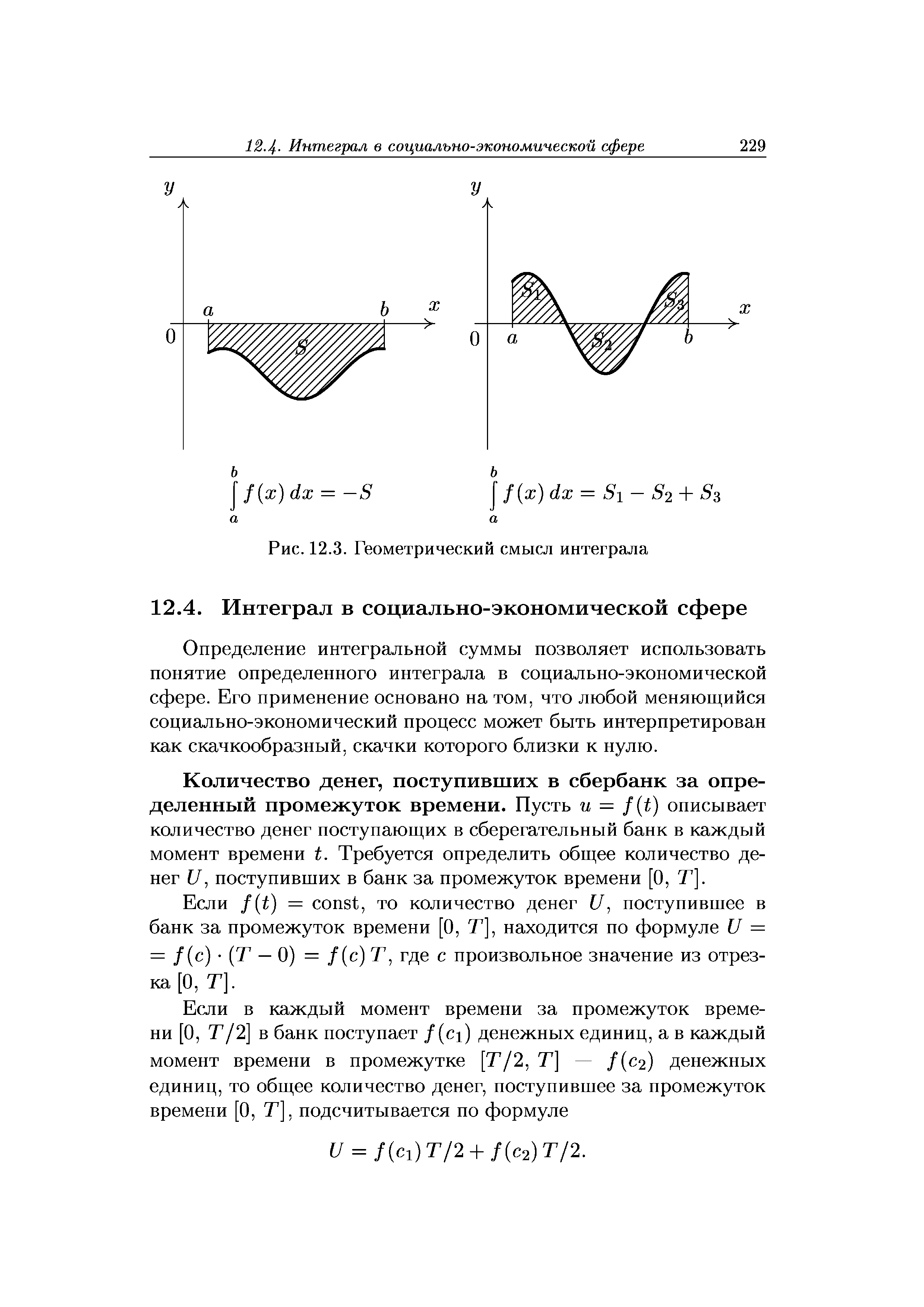 |
Пусть/(ж) 0 на отрезке [а, 6]. Тогда значение функции Ф (ж) в точке х равно площади S(x) под кривой у = /(ж) на отрезке [а, х] (см. рис. 12.5, б). В этом состоит геометрический смысл интеграла с переменным верхним пределом. [c.237]
При а < с < Ъ это равенство имеет простой геометрический смысл (см. рис. 12.4, а). Согласно геометрическому смыслу определенного интеграла [c.233]
Геометрический смысл несобственного интеграла (12.3) для неотрицательной на [а, +оо) функции /(ж) состоит в том, что он представляет собой площадь криволинейной фигуры, ограниченной данной линией у = /(ж), осью Ох и вертикалью х = а. [c.262]
| Рис. 12.17. Геометрический смысл несобственного интеграла | 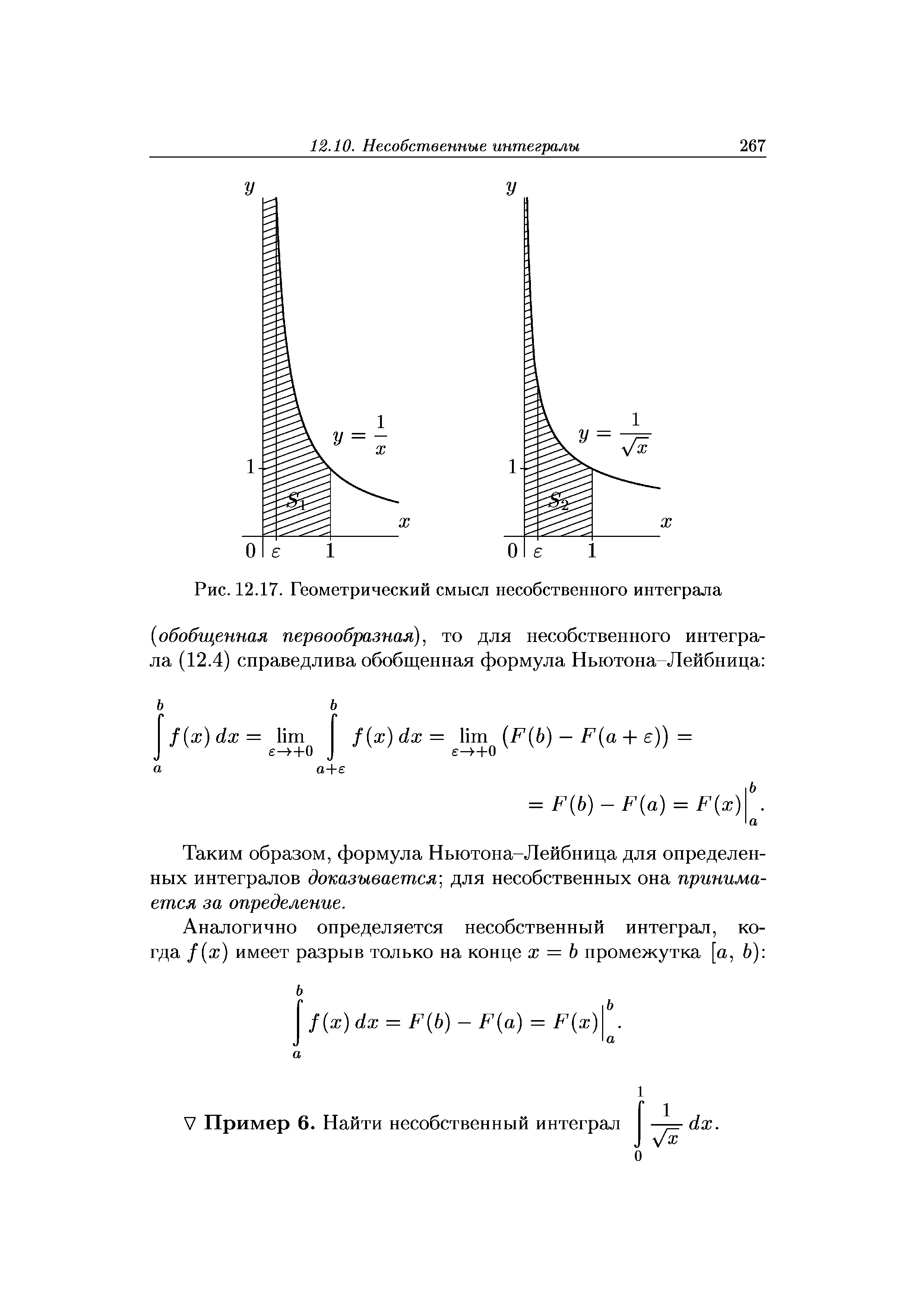 |
Смотреть главы в:
Математика для социологов и экономистов Учебное пособие -> Геометрический смысл интеграла
