Каждое из приведенных выше преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наделены и постоянные числа, входящие в приведенные формулы). [c.119]
Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, т.е. найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи и с описанными выше частными случаями разбивают на несколько этапов. [c.122]
Геометрический смысл условия (1.5) ясен из рис. 1.5. [c.10]
Геометрический смысл этой теоремы проиллюстрирован на рис. 2.2 [c.47]
Геометрический смысл формулы [c.51]
Рассмотрим геометрический смысл условий (11.3) и (11.4) [c.75]
Мы можем измерить степень абсолютной чувствительности переменной у к изменениям переменной х, если определим соотношение Ay/Ах. Недостаток такого определения чувствительности состоит в том, что она зависит не только от "начальной" точки XQ, относительно которой рассматривается изменение аргумента, но и от самой величины интервала Dx, на котором определяется скорость. Для устранения этого недостатка вводится понятие производной (скорости изменения функции в точке). При определении скорости изменения функции в точке сближают точки XQ и xj, устремляя интервал Дх к нулю. Скорость изменения функции f(x) в точке XQ и называют производной функции f(x) в точке х Геометрический смысл скорости изменения функции в точке XQ в том, что она определяется углом наклона касательной к графику функции в точке XQ. Производная — это тангенс угла наклона касательной к графику функции. [c.84]
Геометрический смысл теоремы 4.1 лучше всего раскрывается в случае, когда критерии линейные. Пусть т = 2, п = 2, Мх) = (с1, х), /2(х) = (с2,х), где с с х е R2 (рис. 4.1). [c.96]
Предельная склонность к потреблению (МРС), как отмечалось выше, отражает размер дополнительного потребления, вызванного дополнительным доходом. На графике это выражается в наклоне кривой потребления крутой наклон означает высокую МРС, а плавни наклон — низкую МРС. На рис. 1 виден маленький треугольник, обозначенный пунктирными стрелками, при возрастании дохода от 4000 до 5000 долл. Этот треугольник наглядно показывает геометрический смысл категории предельной склонности к потреблению. Допустим, при возрастании дохода с 4000 до 5000 долл. на потребление расходуется 850 долл. Следовательно, МРС будет составлять 850 долл./1000 долл. =0,85 долл. Приведем укрупненное изображение МРС (рис. 3), равной 0,85, т.е. маленького треугольника из рис. 1. [c.236]
Рассмотрим геометрический смысл предела функции в точке. Построим график функции у = /(ж), точки ж = а, у = Ь. Выберем е > 0 и построим прямые у = b + е, у — b — е. Число 6 является пределом функции /(ж) в точке ж = а, если найдется J-окрестность точки а такая, что часть графика функции /(ж), для которой ж G (а — 6, a) U (а, а + <5), попадает внутрь полосы, ограниченной прямыми у = b — е и у = b + е. [c.58]
Геометрический смысл производной. Для функции у = f(x] ее производная у1 — f (x] для каждого значения х равна угловому коэффициенту касательной к графику функции в соответствующей точке. [c.108]
Будем перемещать секущую А В параллельно начальному положению до тех пор, пока она не превратиться в касательную к графику функции у = f(x) в некоторой точке (7(с, /(с)), где а < с < b (здесь опускается доказательство того факта, что такое предельное положение существует). Согласно построению и геометрическому смыслу производной tg а равен тангенсу угла наклона касательной / (с), поэтому [c.129]
Геометрический смысл теоремы. Если в некотором промежутке касательная к графику функции у = /(ж) образует с осью Ох острый угол a (tga > 0), то функция строго возрастает в этом промежутке. Если касательная к графику функции у — = /(ж) образует с осью Ох тупой угол a (tga < 0), то функция строго убывает (рис. 9.1). [c.141]
| Рис. 10.1. Геометрический смысл эластичности |  |
Напомним, геометрический смысл производной f (x) — это тангенс угла наклона касательной к графику функции у = f(x] в точке С(хС УС], ус = f(x . Геометрический смысл эластичности функции f(x) в точке хс связан с разбиением данной касательной на отрезки точками А, В и С, где А(ха, 0) — точка пересечения касательной с осью Ох, -6(0, г/ ) — точка пересечения касательной с осью Оу (рис. 10.1). [c.194]
Геометрический смысл интеграла [c.228]
| Рис. 12.3. Геометрический смысл интеграла | 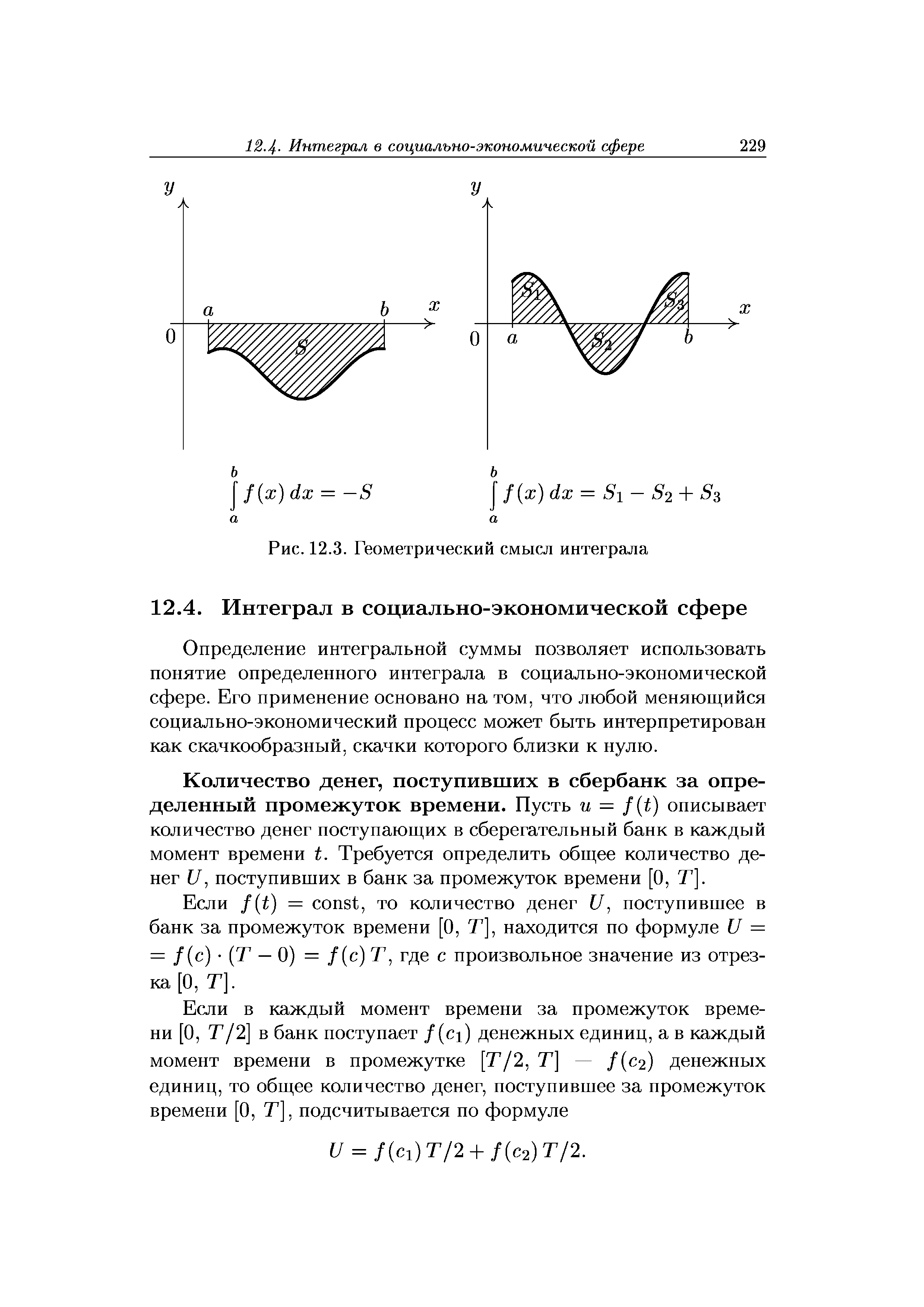 |
Геометрический смысл теоремы о среднем. Пусть [c.236]
Пусть/(ж) 0 на отрезке [а, 6]. Тогда значение функции Ф (ж) в точке х равно площади S(x) под кривой у = /(ж) на отрезке [а, х] (см. рис. 12.5, б). В этом состоит геометрический смысл интеграла с переменным верхним пределом. [c.237]
Геометрический смысл несобственного интеграла (12.3) для неотрицательной на [а, +оо) функции /(ж) состоит в том, что он представляет собой площадь криволинейной фигуры, ограниченной данной линией у = /(ж), осью Ох и вертикалью х = а. [c.262]
| Рис. 12.17. Геометрический смысл несобственного интеграла | 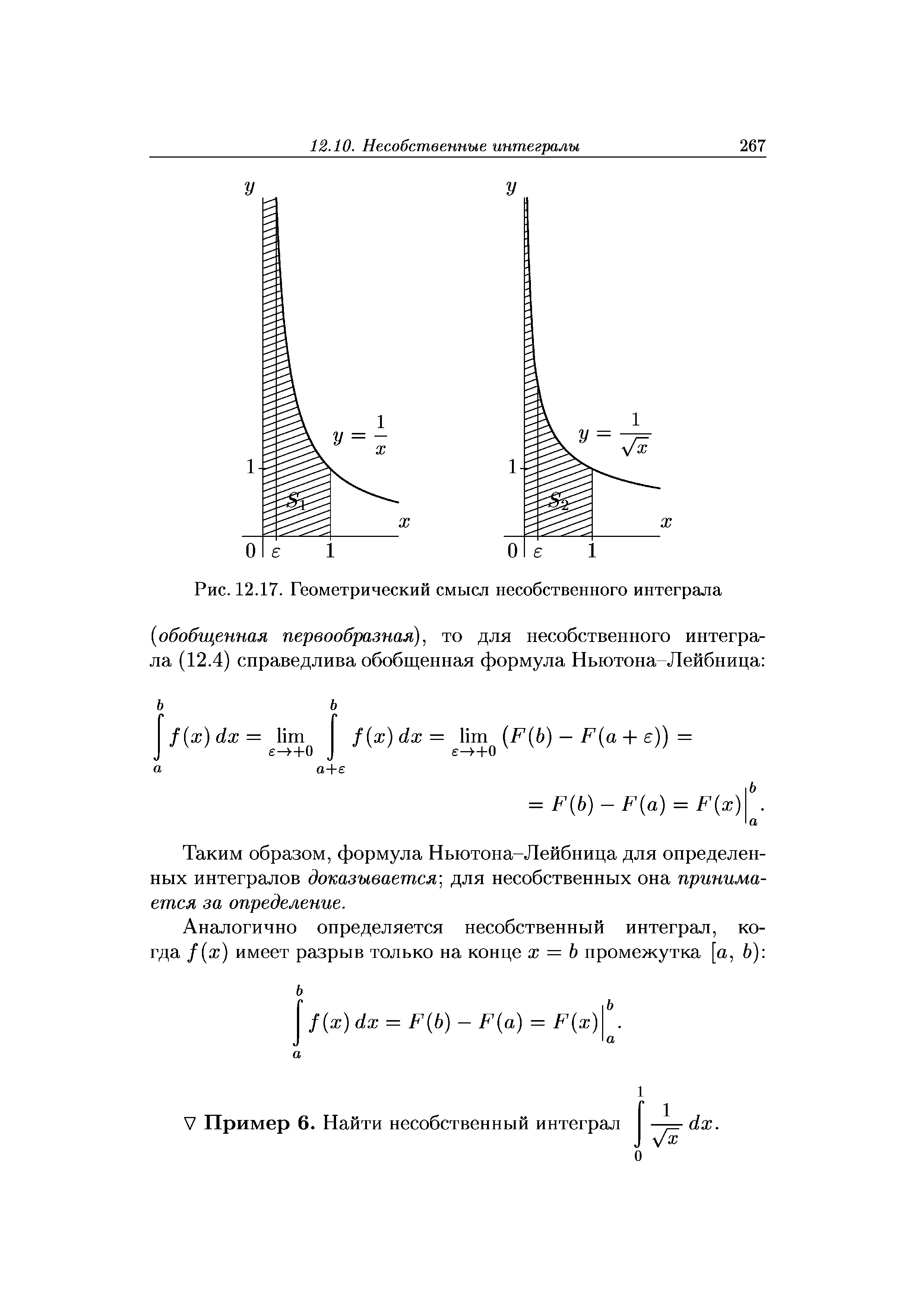 |
Теорема 2 (геометрический смысл необходимых условий экстремума). В стационарной точке касательная плоскость к поверхности z — /(ж, у] параллельна плоскости хОу. [c.307]
Из этого определения и геометрического смысла производной следует, что интегральная кривая уравнения (17.3) полностью лежит в области, в которой определена функция /, и что интегральная кривая в каждой своей точке М(х, у) имеет касательную, угловой коэффициент которой равен значению функции / в этой точке М. [c.360]
Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши (17.3), (17.4) означает найти интегральную кривую уравнения (17.3), которая проходит через данную точку Мо(жо, [c.360]
Геометрический смысл этой теоремы заключается в том, что при выполнении условий теоремы через заданную точку (жо, у о) на координатной плоскости проходит единственная интегральная кривая с заданным угловым коэффициентом уо ее касательной. [c.370]
Геометрический смысл градиента 295 [c.457]
Для выяснения геометрического смысла теоремы Лагранжа заметим, что левая часть (8АЛ) есть угловой коэффициент секущей, проходящей через точки А (а, /(а)) и В ( ,/( )) кривой у = f(x), a правая часть есть угловой коэффициент касательной к той же кривой в точке С ( , /(О)- Теорема Лагранжа о среднем значении функции утверждает, что на кривой у = f(x) между точками А я В всегда найдется такая точка С, касательная к которой параллельна секущей АВ (рис. 8А.1). [c.344]
Доказательство. Выясним геометрический смысл величины d, которую здесь будем обозначать точнее d (х), x( Q. Рассмотрим прямую, соединяющую (в гиперплоскости G, проходящей через х ортогонально g) начало координат с точкой XG, она имеет вид Чхд. Найдем в Q точку у из условия т т(у, %в) про- [c.446]
Рис. 80, а) поясняет геометрический смысл величины d (х). Наконец, рис. 80, Ъ) поясняет, почему при больших размерах Q ситуация d (х) d требует очень точного приближения точки х к точке минимума х величины x g, xf Q. [c.448]
Терминология для сумм, используемых в столбце источник-изменчивости , в разных работах разная. Так, вместо термина между градациями употребляют термины между совокупностями , между способами обработки вместо термина ошибка говорят о сумме квадратов внутри групп , внутри совокупностей , остаточной сумме квадратов. 13.2.2. Геометрический смысл ДА. Хотя общие вопросы проверки гипотез в случае линейной регрессии уже рассмотрены в гл. 7, представляется интересным конкретизировать их в случае однофакторной модели ДА. Положим [c.377]
Если величины доходности ценных бумаг отобразить в виде точек на числовой оси, а вероятности каждого из значений интерпретировать как вес каждой из точек, то в геометрическом смысле математическое ожидание будет представлять собой центр тяжести всей такой системы. [c.247]
Равенство (3.26) имеет простой геометрический смысл. Построим в Rn+i график функции f(x) у =f(x) и график линейной функции у = х х (рис. 14). Величина —/ ( ) есть минимальное расстояние между ними по вертикали. [c.96]
Соотношение (5.11) имеет простой геометрический смысл. Оно означает, что в первом приближении поперечное сечение стержня после деформации остается перпендикулярным к деформированному положению средней линии стержня. [c.138]
Для ответа на первый вопрос мы рассмотрим определение и геометрический смысл производной, формулы для нахождения производных нескольких простейших (элементарных) функций и правила дифференцирования, позволяющие находить производные от любых комбинаций элементарных функций. [c.48]
| Рис. 1.18. Гауссовая кривая нормального распределения (геометрический смысл среднего значения и среднего отклонения (i = liirn/). |  |
Выясним геометрический смысл условия (2.51). Для этого воспользуемся представлением ортогональных матриц (1.3.26). Из (1.3.26) следует, что Хд= 1 + 2 os9, где в — угол поворота вокруг оси вращения. Согласно (2.51) ose > 0, и неравенство (2.51) означает, что однозначное решение уравнений (2.47) можно выделить условием материальные волокна поворачиваются на углы, не превосходящие л/2. [c.172]
Геометрический смысл скорости изменения функции на интервале (х0 х) (средней скорости) в том, что она численно равна тангенсу угла наклона отрезка, соединяющего две точки графика функции, соответствующих значениям аргумента х0 и х, т.е. тангенсу угла а в треугольнике M0MN( M. рис. 3.16). [c.50]
Смотреть страницы где упоминается термин Геометрический смысл ДА
: [c.293] [c.189] [c.403] [c.406] [c.427]Смотреть главы в:
Прикладная статистика Исследование зависимостей -> Геометрический смысл ДА
