В аффинных преобразованиях плоскости особую роль играют несколько важных частных случаев, имеющих хорошо прослеживаемые геометрические характеристики. При исследовании геометрического смысла числовых коэффициентов в формулах ( ) для этих случаев удобно считать, что заданная система координат является прямоугольной декартовой. [c.118]
| Таблица 17.2 Геометрическая характеристика стальных труб и их масса | 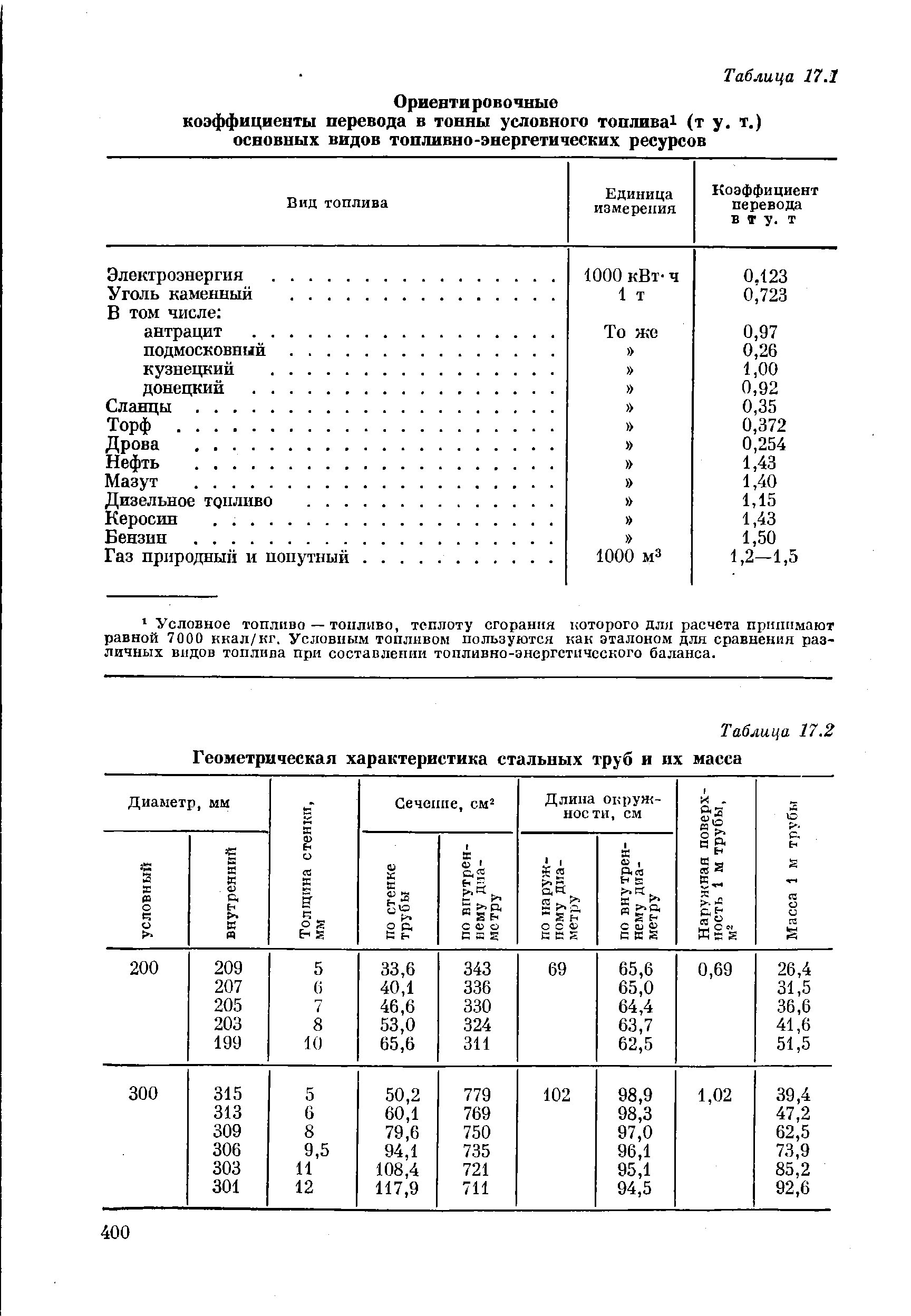 |
По каждой машине в базе данных хранятся следующие данные характеристика изделия (наименование, шифр (модель, марка), геометрические характеристики, производитель, потребитель, условия эксплуатации, перечень узлов и агрегатов, данные по отказам данные по определению потребности и управлению запасами запасных частей (место, сроки доставки и спрос). [c.227]
| Рис. 2. Геометрические характеристики эластичности варианты положения касательной к графику функции. | 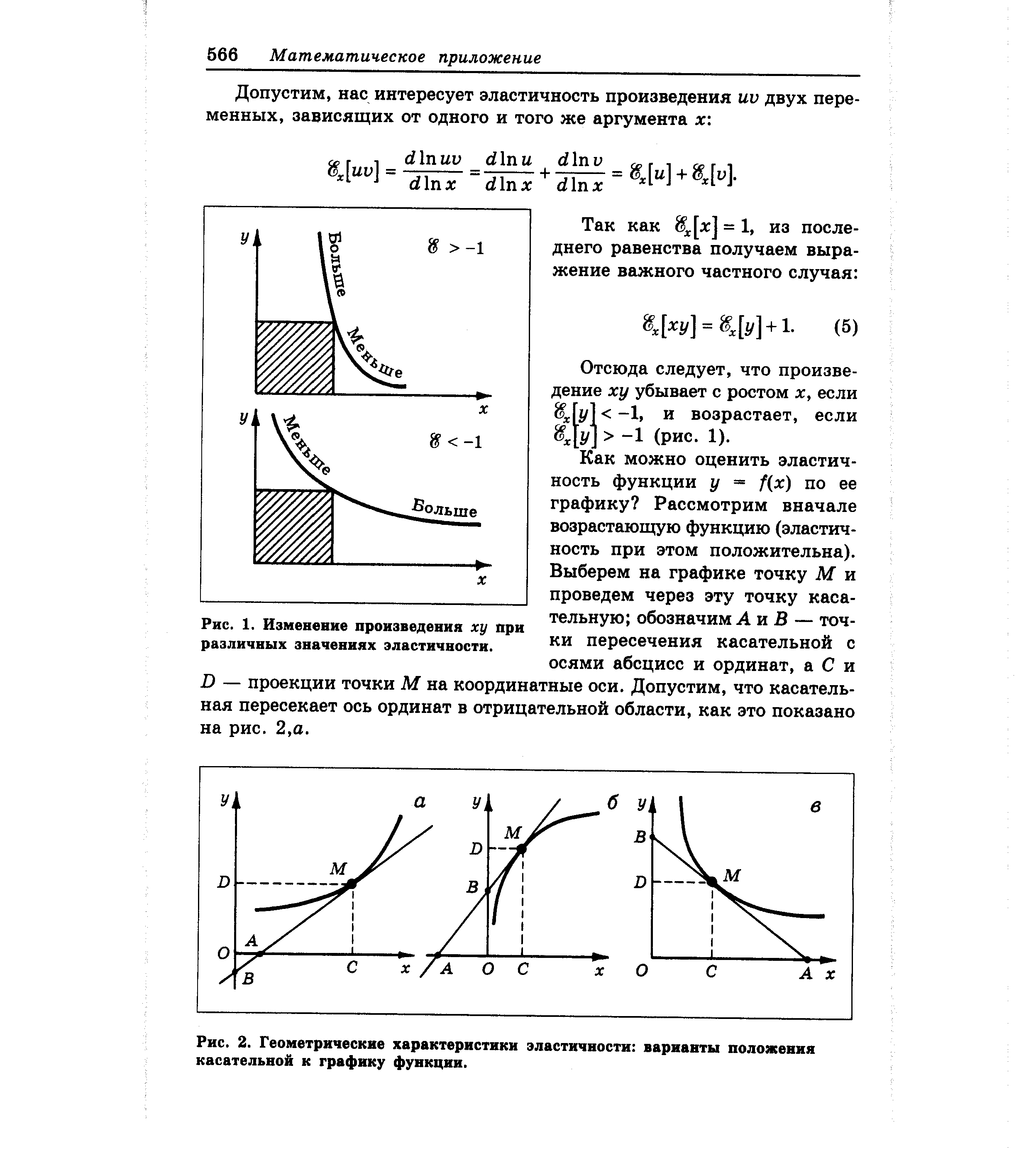 |
Смоляк С. А. Оптимальное восстановление функций и связанные с ним геометрические характеристики множеств. — В кн. Тр. 3 зимней школы по математическому программированию и смежным вопросам. — М. ЦЭМИ АН СССР, 1970, вып. 3, с. 509 — 557. [c.465]
В качестве исходной можно принять следующую систему уравнений и неравенств сегмента (вытекающую из геометрических характеристик планов форм документов) [c.104]
Влияние шага письма и шага строк, наносимых печатающими устройствами. Значения этих двух параметров наиболее часто встречаются в выражениях, определяющих затраты на отдельных операциях работы с документами (см. рис. 3.1). В большинстве случаев функциональная связь затрат с рассматриваемыми параметрами определена из геометрических характеристик формы документов и явно отражена в приведенных в п. 3.3 аналитических выражениях. Исключением являются затраты на чтение документов и перенос данных на машинный носитель. В выражениях (3.48) и (3.58) содержатся величины скорости чтения и переноса данных, но связь их с шагом письма и шагом строк теоретически не раскрыта, хотя она несомненно существует. [c.124]
Средняя скорость чтения машинописного текста в рассмотренном диапазоне изменения его геометрических характеристик равна 28,0 зн./с. [c.126]
Ряд геометрических характеристик объектов (длину улицы, расстояние между городами, площадь лесного массива) можно измерять непосредственно на экране, пользуясь средствами ГИС. [c.81]
Впервые принцип максимального расхода использован в работе [2] при условии, что для расчета центробежной форсунки гидравлические потери внутри форсунки отсутствуют, а момент количества движения, сообщенный жидкости на входе в камеру закручивания, остается неизменным до выхода ее из форсунки. При этих допущениях получены зависимости, необходимые для определения производительности форсунки G, коэффициента расхода ц, и геометрической характеристики А. В дальнейшем эта методика была уточнена и дополнена с учетом вязкости жидкости и потерь на трение о стенки форсунки [82]. [c.83]
На рис. 4.11,6 показана центробежная форсунка, у которой для уменьшения угла раскрытия факела выходной канал выполнен в форме сопла Л аваля, а расширяющаяся часть — по кривой с углом раскрытия, уменьшающимся в направлении движения жидкости. При этом в распыленном факеле происходит перераспределение между осевой, окружной и радиальной составляющими скорости таким образом, что угол раскрытия факела уменьшается независимо от геометрической характеристики форсунки. На рис. 4.11,6 показана форсунка, у которой камера закручивания выполнена в отдельном узле. [c.85]
Совместным решением уравнений (4.38) и (4.42). находим искомое значение коэффициента расхода жидкости р,, который представляем в виде зависимости от геометрической характеристики А и комплекса В (рис. 4.23). На графике пунктиром проведена кривая зависимости i=f(A) для истечения холодной жидкости, которую кривые р/ при различных значениях В пересекают в некоторых точках. Это обусловлено тем, что автор [164] принял зависимость, полученную в работе [2] на основе принципа максимального расхода, который недостаточно полно учитывает конструктивные особенности центробежной форсунки. Поэтому в действительности граница будет определяться не одной характеристикой, а областью характеристик. [c.99]
Указанная особенность связана с тем i[164], что в случае, когда геометрические характеристики велики, а значение комп- [c.99]
| Рис. 4.23. Зависимость коэффициента расхода от геометрической - характеристики форсунки для различных значений комплекса В. |  |
Геометрическую характеристику представим формулой [c.101]
Для центробежных форсунок со шнеком формула (4.43) пригодна только в интервале значений А, при которых площадью, определяющей расход жидкости, является суммарная площадь каналов шнека. Предельное значение геометрической характеристики А, ограничивающее применение (4.43), выражается неравенством [c.101]
Для проверки предлагаемого метода расчета истечения кипящей жидкости через центробежную форсунку с тангенциальным входом и со шнеком в работе [164] использованы данные [115]. Размеры проточной части форсунок с тангенциальным входом составляли диаметр и длина сопла—6 и 30 мм, диаметр и длина камеры закручивания—-27 и 30 мм, диаметр, тангенциального отверстия 10 мм, число отверстий — 2. Шнековая форсунка имела следующие размеры диаметр сопла —2,2 мм, высота и диаметр шнека—16 и 6 мм, число заходов — 3, геометрическая характеристика 0,82. [c.101]
Сопоставление. результатов расчета угла раскрытия факела и коэффициента расхода жидкости в зависимости от геометрической характеристики А (А) для центробежной форсунки, рассчитанной по обеим теориям, представлено на рис. 5.6. [c.120]
Как следует из графиков, коэффициенты расхода-отличаются между собой не более чем на 20% при А=0,33 (А = 0,66). С ростом геометрической характеристики А (или А ) это расхождение уменьшается, и при А = 2 не превышает 10%. Необходимо отметить, что подробные эксперимент-альные исследования центробежных форсунок в этом интервале значений А не проводились. В интервале значении, в котором работает подавляющее большинство центробежных форсунок (на графике заштрихован), т. е. при А >2, отклонение коэффициента расхода составляет всего 4%. Аналогичные изменения по мере роста А наблюдаются и для угла раскрытия факела для большинства центробежных форсунок отклонение р не превышает 10%. [c.120]
Из сравнения прямых 10—14, рассчитанных по этой формуле, и экспериментальных данных видно, что формула описывает значения коэффициентов расхода лишь в определенном интервале геометрической характеристики, не охватывая весь диапазон возможного ее изменения. [c.186]
Остановимся более подробно на результатах исследований магнитострикционной форсунки, приведенных в работе [107]. В опытах расход жидкости изменялся в интервале 0,05—5 кг/ч при давлении в жидкостной линии не более 5 кПа. Результаты исследований показали, что производительность форсунки зависит от амплитуды колебаний рабочего элемента, вязкости и поверхностного натяжения распыливаемой жидкости, способа ее подачи-на рабочую поверхность и ряда геометрических характеристик (диаметра сопла форсунки, площади смачиваемой поверхности и др.). [c.203]
Геометрическая характеристика центробежно-струйных форсунок [c.249]
Все виды моделей можно разделить на две большие группы материальные и абстрактные модели. Материальные модели воспроизводят геометрические, физические и другие функциональные характеристики изучаемого объекта. Абстрактные, или идеальные модели основываются на идеальной, мыслимой аналогии с объектом. Абстрактные модели широко применяются в экономических исследованиях. Их можно разбить на две подгруппы знаковые и интуитивные модели. [c.23]
Просуммировав потери по формулам (5.22) — (5.25) и приравняв давления, получим с,ле.%учялучь ЪЪЪЧАЯМ Х-ГЪ для определения геометрической характеристики с учетом потерь в кана- [c.114]
Как отмечалось, в число исходных данных должны быть включены и дисперсные характеристики. Для вывода расчетных уравнений известные экспериментальные данные, а также данные, полученные авторами, обработаны в виде критериаль-ных уравнений, в которых в качестве геометрического критерия подобия принята геометрическая характеристика центробежно-струйных форсунок А [c.129]
Обобщения, представленные в виде зависимостей (7.3) и (7.4), справедливы для распылителей с различными геометрическими характеристиками, работающих с подводом и без подвода рас-пыливающего воздуха, при следующих параметрах Рж=(3— —30) 102 кПа Рг= (0,5—6) 102 кПа = 0,15—0,54. Однако следует отметить, что показатель степени при скорости w у различных авторов находится в пределах п = 0,34—0,7. [c.162]
Гидравлические характеристики форсунки. На рис. 8.7 приведены зависимости коэффициента расхода от геометрической характеристики завихрителя. Цифрами /—6 обозначены зависимости, объединяющие завихрители с постоянным параметром d3/R 7—9 — зависимости, объединяющие завихрители с постоянным параметром R/R , 10—14 — зависимости, построенные по формуле для расчета среднего диаметра капель. [c.186]
| Рис. 8.7. Зависимость коэффициента расхода от геометрической характеристики завихрителя |  |
| Рис. 8.8. Зависимость порогового значения числа Ren от геометрической характеристики завихрителя. |  |
