Поскольку дискриминантная функция зависит лишь от линейной комбинации входов, нейрон является линейным дискриминатором. В некоторых простейших ситуациях линейный дискриминатор - наилучший из возможных, а именно - в случае когда вероятности принадлежности входных векторов к классу k задаются гауссовыми распределениями [c.51]
Здесь мы ввели коэффициент а = (х Д, - у < 1. Например, для Гауссова распределения [c.158]
Определение коэффициента угрозы краха. Симуляция с использованием компьютерной программы идет следующим образом. Во-первых, мы выбираем дискретизацию времени с шагом St. Затем, зная величину случайных блужданий W(t-St) и цену B(t-8t) в предшествующее время t-dt, мы выводим W(t), прибавляя приращение, взятое из центрированного гауссова распределения с вариацией St. Отсюда мы выводим цену B(t), взяв величину, обратную (W -W(t))a, где - положительный показатель степени, определенный в модели. Затем мы выражаем, при условиях отсутствия арбитража и рациональных ожиданиях, вероятность h(t) возникновения краха во время следующего временного этапа, где h(t) - коэффициент угрозы краха. Мы сравниваем данную вероятность со случайным числом гаи, равномерно выбранным в интервале [0,1] и запускаем механизм краха, если ran < h(t)St. В данном случае цена B(t) меняется на B(t)(l-K), где к взято из предварительно выбранного распределения. Например, спад к при крахе может быть зафиксирован на уровне, скажем, 20%. Слишком прямолинейно сводить это к арбитражному распределению скачков. После краха динамика продолжается с бесконечно малым приращением, как и раньше, начиная с этого нового значения для времени t, после соответствующего переноса W(t), чтобы обеспечить непрерывность цен. Если ran > h(t)St, краха не происходит и динамика повторится на следующем временном шаге. [c.171]
Для каждого агрегата или технологической линии, электропотребление которых фиксируется по счетчикам, удельные расходы на единицу продукции могут быть рассчитаны за каждые сутки (или технологическую операцию) и за год (месяц, квартал). Эти показатели имеют гауссово распределение, которое [c.109]
Сделайте первое приближение Z к u(o,F), взяв взвешенное среднее значение F квантилей распределений Коши и гауссовых распределений. [c.277]
Мы выяснили в гл. 5, что для данных с нормальным, или Гауссовым, распределением разность между переменной и ее средней, деленная на оценку ее среднего квадратического отклонения, имеет /-распределение. Таким образом, оценки, деленные на стандартные ошибки, как рассчитано ранее, имеют г-распре-деление с п—2 степенями свободы. Опираясь на эту информацию, можно определить доверительные интервалы вокруг точечных оценок коэффициентов. [c.274]
Нормальное распределение. Нормальное, или гауссово распределение, - это, несомненно, одно из наиболее важных и часто используемых видов непрерывных распределений. Оно симметрично относительно математического ожидания. Сначала остановимся на практическом смысле этого распределения применительно к экономическим задачам и сформулируем центральную предельную теорему теории вероятностей в следующей практической интерпретации. [c.28]
Понятно, что само по себе снижение капитализации в контексте более широких объективных причин, таких как всеобщий спад на рынке, крупные скандалы, не относящиеся к данной компании, но формирующие преобладающее настроение рынка, и пр., не может служить основанием требовать возмещения ущерба. Поэтому исключительно важно для доказательной базы, чтобы экспертная оценка недобросовестности публикаций, повлекших падение капитализации, была выполнена на высоком научном уровне. К примеру, недостаточно ограничиться сопоставлением наблюдаемой капитализации и реконструкцией по тренду, если в качестве тренда выступает коридор, заданный нормальным (Гауссовым) распределением доходности, если при этом не учитывается сложная комбинированная природа тренда, включающего в себя дополнительные случайные процессы. [c.417]
На рисунке хорошо видны как высокий пик в окрестности среднего значения доходности, так и толстые хвосты функции плотности распределения. С точки зрения гауссова распределения вероятность появления событий, значительно уклоняющихся от средних значений, — так называемых выбросов — экспоненциально уменьшается и практически равна нулю на всех масштабах. Тем не менее рынки демонстрируют нам такие события на всех масштабах, и не учитывать их — значит существенно недооценивать риски. [c.203]
Выбор показателя I) зависит от вероятности, с которой мы желаем определить границы доверительного интервала. Так, например, в случае гауссова распределения величины выбор D=l соответствует тому, что цены закрытия окажутся внутри интервала от Р (Т) до Pt(T) с вероятностью 68%. Это достаточно небольшая вероятность, и котировки часто будут выходить за построенные таким образом границы. Для вероятности 95% необходимо выбрать D= 1, 65. Наконец, если мы желаем найти границы, за которые цены не выйдут с вероятностью 99%, следует выбрать D= 2,33. [c.489]
В качестве альтернативы методу СОК с гибридным обучением мы могли бы окрасить плоскости признаков таким образом, чтобы цвет каждого элемента карты определялся свойствами отображаемых на него векторов данных. Однако этот путь привел бы к возникновению случайных цветовых вариаций по причине статистических помех. При использовании описанного выше подхода с гибридным обучением этого не происходит, поскольку функция гауссова распределения позволяет сгладить эти случайные вариации. [c.107]
Обычно принимают, что для активного развитого фондового рын справедливо так называемое нормальное (гауссово) распределение шк ности вероятности доходности [c.68]
Ключевым понятием при измерениях становится термин "допустимые отклонения". Существуют различные методики установления значений для допустимых отклонений. Все эти методики используют аппарат математической статистики и теории вероятностей. Наиболее часто применяется так называемое гауссово распределение вероятностей, для которого среднеквадратичное отклонение обозначается греческой буквой сигма — а. Соответственно, модели бизнес - контроля часто называются За, 6о. [c.71]
Кривую нормального закона распределения называют нормальной или гауссовой кривой (рис. 2.4). [c.34]
Чем дальше, тем сильнее в такой ситуации люди будут стремиться получить такую счетную единицу, изменение ценности которой было бы более тесно увязано с общей тенденцией, и даже, быть может, вынуждены будут использовать в качестве счетной единицы что-то такое, что нельзя использовать в качестве средства обмена. (Кривая, представляющая дисперсию изменений цен в виде доли всех продаж, произведенных за определенный период по возросшим или снизившимся по сравнению с предыдущим периодом ценам, будучи построена по логарифмической шкале, должна, конечно, иметь одну и ту же форму, независимо от того, используем мы в качестве измерителя цен деньги или какой-нибудь товар. Если мы используем в качестве стандарта товар, цена которого упала больше, чем цена любого другого, все изменения цен будут выглядеть как повышения, однако рост относительной цены одного товара по сравнению с другим будет оставаться одним и тем же, скажем, 50 процентов, какую бы систему мер, мы ни выбрали. Мы, вероятно, получим кривую в виде нормальной (гауссовой) кривой распределения ошибок. Случайные отклонения от нее в ту или другую сторону, насколько мы способны предсказать, будут взаимно погашаться, и количество их будет уменьшаться с ростом величины отклонения. (Большинство ценовых изменений будет вызываться смещением спроса с соответствующим падением некоторых цен и повышением других относительно мелкие смещения такого рода будут, вероятно, более частыми, чем крупные.) Общий уровень цен, выраженный в деньгах со стабильной в данном смысле ценностью и представленный данной кривой, не должен в этом случае меняться, а объемы сделок, совершаемых по ценам, возросшим или упавшим на некоторый процент, должны уравновешивать друг друга. Это минимизирует ошибки - не обязательно отдельных индивидуумов, но всего общества в целом. И хотя никакое индексное число, обычно исчисляемое для этих целей, не поможет полностью подтвердить то, что мы предположили, достаточно точное приближение к измерению такого эффекта вполне достижимо.) [c.61]
Фрактальная размерность временного ряда важна, потому что она признает, что процесс может быть где-то между детерминистическим (линия с фрактальной размерностью 1) и случайным (фрактальная размерность 1,50). Фактически, фрактальная размерность линии может находиться в пределах от 1 до 2. При значениях 1,50 < d < 2 временной ряд более зазубрен, чем случайная последовательность, или имеет больше инверсий. Само собой разумеется, статистика временного ряда с фрактальными размерностями, отличными от 1,50, сильно отличалась бы от гауссовой статистики и не обязательно находилась бы в пределах нормального распределения. [c.26]
Когда инвестиционный горизонт становится однородным, рынок входит "в свободное падение" то есть, в последовательности ценообразования появляются разрывы. В гауссовой окружающей среде большое изменение является суммой многочисленных небольших изменений. Однако во время паники и панических бегств рынок часто перескакивает через цены. Разрывы вызывают большие изменения, и в частотном распределении прибылей появляются жирные хвосты. Эти разрывы, в свою очередь, являются результатом недостатка ликвидности, вызванного появлением однородного инвестиционного горизонта для участников рынка. [c.56]
Стандартная гауссова статистика лучше всего работает на основе весьма ограничивающих предположений. Центральная предельная теорема (или Закон больших чисел) утверждает, что по мере проведения все большего числа испытаний, предельное распределение случайной системы будет нормальным распределением, или колоколообразной кривой. Измеряемые события должны быть "независимы и идентично распределены" (IID). То есть события не должны влиять друг на друга, и они все должны иметь одинаковую вероятность наступления. Долгое время предполагалось, что большинство крупных, комплексных систем должны моделироваться таким образом. Предположение о нормальности, или почти нормальности, обычно делалось при исследовании крупной, комплексной системы, так чтобы мог быть применен стандартный статистический анализ. [c.61]
Проверка гипотезы постулирует наиболее вероятный результат в качестве возможного ответа. Если мы не понимаем механики определенного процесса, например, фондового рынка, то статистическая структура, которая является независимой и идентично распределенной (IID) и характеризуется случайными блужданиями - наше лучшее первое предположение. Структура является гауссовой, и ее распределение плотности вероятности является нормальным распределением, или колоколообразной кривой. Это первоначальное предположение называют нулевой [c.73]
Мы начнем с ряда псевдослучайных чисел, содержащего 5 000 значений (нормально распределенных с нулевым средним и стандартным отклонением равным единице), которые дважды перемешиваются. Мы вычисляем значения R/S для всех п, которые являются ровно делимыми на 5 000 то есть каждое значение R/Sn будет всегда включать начальное и конечное значение полного временного ряда. Затем мы повторяем этот процесс 300 раз, так чтобы у нас было 300 значений R/Sn для каждого п. Среднее этих R/Sn - ожидаемое значение E(R/Sn) для системы гауссовых случайных чисел. Рассчитываются дисперсии, и конечные значения сравниваются со значениями, полученными с использованием уравнений (5.1), (5.2) и (5.3). Результаты показаны в таблице 5.1 и графически изображены на рисунке 5.1. [c.75]
Что, если независимый процесс отличается от гауссова процесса Как мы видели в таблице 5.2, независимое распределение с толстыми хвостами и высоким пиком действительно обнаруживает средние значения, как они были предсказаны в уравнении (5.6). Тем не менее, дисперсия все-таки отличается. К сожалению, дисперсия для распределений, которые не являются нормально распределенными, отличается на индивидуальном основании. Поэтому наш доверительный интервал [c.80]
Первоначально стандартное отклонение использовалось потому, что оно измеряло дисперсию процента изменения цен (или прибылей) распределения вероятностей. Распределение вероятностей оценивалось на основании ненормализованных эмпирических данных. Чем больше стандартное отклонение, тем выше вероятность большого изменения цены - и тем рискованнее акция. Кроме того, полагалось (по причинам, обсуждавшимся ранее), что выборка прибылей осуществлялась из нормального распределения. Вероятности могли быть оценены на основании гауссовой нормы. Также предполагалось, что дисперсия была конечна следовательно, стандартное отклонение стремилось бы к значению, которое было стандартным отклонением совокупности. Стандартное отклонение было, конечно, выше, если временной ряд цен был более изрезан, поэтому стандартное отклонение стало известным как мера волатильности акций. Тот факт, что акция, склонная к сильным колебаниям, будет более волатильной и более рискованной, чем менее волатильная акция, казался исключительно разумным. На рисунке 10.1 показано пересчитанное на год стандартное отклонение 22-дневных прибылей для индекса S P 500 со 2 января 1945 г. по 1 августа 1990 г. [c.143]
Мы неоднократно говорили о том, что нормальное распределение не подходит для описания рыночных прибылей. До настоящего времени мы конкретно не говорили, что должно его заменить. Мы сделаем предположение, которое не поправится многим читателям. Во-первых, мы должны повторно исследовать причины широкого признания гауссовой гипотезы (рынки - случайные блуждания, которые хороню описываются с помощью нормальною распределения). [c.191]
Одно из них было предложено в 1985 году Кинцелем, который основывал свои рассуждения на реальном наблюдении, согласно которому у ребенка в первые несколько лет жизни отмирает большое число синапсов, хотя именно в это время он учится и усваивает огромное количество информации (Kinzel, 1985). Подобное явление подсказало Кинцелю следующий метод обучения. Возьмем полностью неорганизованную сеть нейронов
При использовании вероятностных моделей риска распространены два характерных заблуждения. Во-первых, если величина ущерба зависит от множества причин, то она должна иметь нормальное распределение. Это ошибочное мнение, так как все зависит от способа их взаимодействия. Если причины действуют аддитивно (суммарно), то согласно Центральной предельной теореме теории вероятностей величина ущерба действительно имеет приблизительно нормальное (гауссово) распределение. Если же причины действуют мультипликативно, то в силу той же теоремы следует приближать распределение величины ущерба X с помощью логарифмически нормального распределения. Если же основное влияние оказывает слабое звено , то согласно теоремам, доказанным академиком Б. В. Гнеденко, величину ущерба Xследует описывать с помощью распределения из семейства Вейбулла—Гнеденко. [c.276]
Ошибка показывает, на сколько мы можем ошибиться при планировании. Обычно ошибки подчиняются стандартному Гауссовому распределению. А это означает, что с вероятностью [c.41]
Как сказал Федер (Feder, 1988) "Положение X(t) находится, если дано положение X(to), посредством выбора случайного числа е из гауссова распределения, умножая его на приращение времени t - t of1 и прибавляя результат к данному положению X(t<))". [c.179]
Пока на рынке присутствуют покупатели и продавцы, будут существовать спрос и предложение на конкретную ценную бумагу. Всегда найдутся желающие купить по цене, которая кому-то кажется разумной, и всегда найдутся желающие продать. Баланс спроса и предложения определяет цену в каждый конкретный момент времени. Этот баланс подвержен внешним влияниям. Положительные и отрицательные новости и события изменяют представления игроков о стоимости ценной бумаги и сдвигают баланс в ту или иную сторону. Поскольку каждый инвестор действует по собственным побуждениям, на которые влияет множество внешних и внутренних факторов, цены меняются на первый взгляд достаточно хаотично. Некоторые исследователи фондового рынка утверждают, что движение цен на небольших временных интервалах походит на траекторию блужданий броуновской частицы. Иными словами, отклонение цены от первоначального значения есть случайная величина, подчиняющаяся гауссовому распределению со среднеквадратичным отклонением, прямо пропорциональным корню квадратному из времени. Мы еще вернемся к этой теме в частях VI и VII, где будут рассматриваться особенности торговли на коротких временных интервалах. Что же касается больших интервалов времени, то здесь нет места хаосу. Об этом уже говорилось в гл. 19 и 21. Более того, сам предмет настоящей главы — тренды ценных бумаг — достаточно красноречиво опровергает представления сторонников теории хаоса. [c.240]
Помимо гауссового распределения в аналитике, особенно при определении следовых количеств, некоторую роль играет и логарифмическое нормальное распределение. Асимметрия этого распределения вносит две особенности [c.41]
Предположение гауссовости распределений Law(/ii,. . ., Л ) величин hi, . . . , Л является, конечно, наиболее привлекательным и с точки зрения теоретического анализа, и с точки зрения хорошо развитой "статистики нормального распределения Но, как отмечалось выше, приходится констатировать (и считаться с этим), что статистическая обработка данных многих финансовых рядов показывает, что предположение гауссовости не всегда адекватно отражает истинную картину поведения цен. [c.129]
Важно подчеркнуть, что сумма, стоящая в (2), есть сумма случайного числа случайных величин, распределение которой может быть достаточно сложным, даже когда отдельные составляющие и случайное число членов имеют сравнительно простые распределения. Это обстоятельство может рассматриваться как некоторое формальное объяснение того, что, как будет доказано далее, распределение величин h не может считаться гауссовским. Правда, мы увидим, что при увеличении А, влекущем за собой увеличение числа членов в сумме в (2), гипотеза о гауссовости распределений величин /4 становится более правдоподобной - начинает "сказываться" феномен справедливости центральной предельной теоремы при суммировании большого числа слагаемых. [c.395]
Многочисленные исследования показывают, что доходности действительно не подчиняются гауссовому распределению, а описываются так называемыми распределениями с толстыми хвостами и высокими пиками. Общий класс этих распределений называется распределениями Псрето — Леей. Эти распределения реализуются на любых масштабах. Высокий пик распределения свидетельствует о наличии памяти- на рынке (и, следовательно, говорит о применимости технического анализа, см. часть IV). С другой стороны, толстые хвосты распредел ими определяют высокую вероятность появления на рынке событий от 4о" до бет, т.е. событий, отклоняющихся от средних на величину от 4 до б среднеквадратичных отклонении. Эти события легко могут быть найдены на любом масштабе. Так называемые крахи (или катастрофы, а также спекулятивные пузыри) на дневных или недельных графиках представляют собой именно такие события. Существенные провалы и всплески котировок, вызванные спекулятивным сбросом или скупкой бумаг (как говорят трейдеры, проливами и выносками ), достаточно часто встречаются на внутридневных графиках и на своем масштабе также являются событиями с большими сигма. На рис. 19.4 показано реальное распределение дневных доходностей индекса РТС и аппроксимирующее его нормальное распределение. [c.202]
Это свойство непосредственно касается возможности определять с помощью границ Боллинджера границы зоны риска (см. гл. 19). Если бы цены, на основании которых вычисляются границы Боллипджера, подчинялись гауссовому распределению, то коэффициент смещения d определял бы границы доверительного интервала, внутри которого должны были бы находится котировки с той пли пион вероятностью. В частности, при d= 2 цены должны были бы находиться внутри границ Боллинджера с вероятностью 95.4%. Однако цены не подчиняются нормальному распределению. Ьолее того, нормальному распределению не подчиняются даже доходности, что не позволяет аппроксимировать распределение цеп логнормальным законом. Исследования рынков на разных временных интервалах показывают, что поиск вида распределения представляет нетривиальную задачу, которая должна решаться заново для каждого вида финансового актива. [c.294]
Если качество данных является неожиданно низким, интерпретатор совместно с обработчиком должен оценить набор данных, чтобы решить, как повысить отношение сигнал/помеха. Существует множество вариантов. Самый простой способ повышения величины S/N - это увеличение бинов. В традиционной 3-D съемке, это обычно означает, что бин должен быть увеличен в два или в четыре раза. В последнем случае, кратность возрастает вчетверо, а отношение сигнал/помеха - вдвое (рис.10.21). Если многие выносы являются избыточными, или если состав выносов плохой, увеличение S/N может оказаться не таким большим, как ожидалось. Отметим, что линейные помехи, связанные с источником, не подчиняются гауссову распределению, и, следовательно, величина S/N для этих конкретных помех не возрастет с увеличением кратности. [c.209]
Исходя из этого, поиск нейрона-победителя будет осуществляться с использованием только той части вектора, которая содержит финансовые показатели, взятые из финансовых отчетов, в то время как для обновления весов элементов карты будет использоваться весь вектор целиком. Для обновления весов мы воспользовались гауссовым распределением меры соседства, так как в сравнении с другими известными методами оно дает более гладкое отображение — так называемое пузырьковое распределение меры соседства (bubble neighborhood), облегчающее визуальное исследование. [c.107]
| Рис. 3.10. Нормальное (гауссово) распределение вероятности значений доходности в пределах а находится 68,3% измеренъ (наблюдений) доходности ценных бумаг | 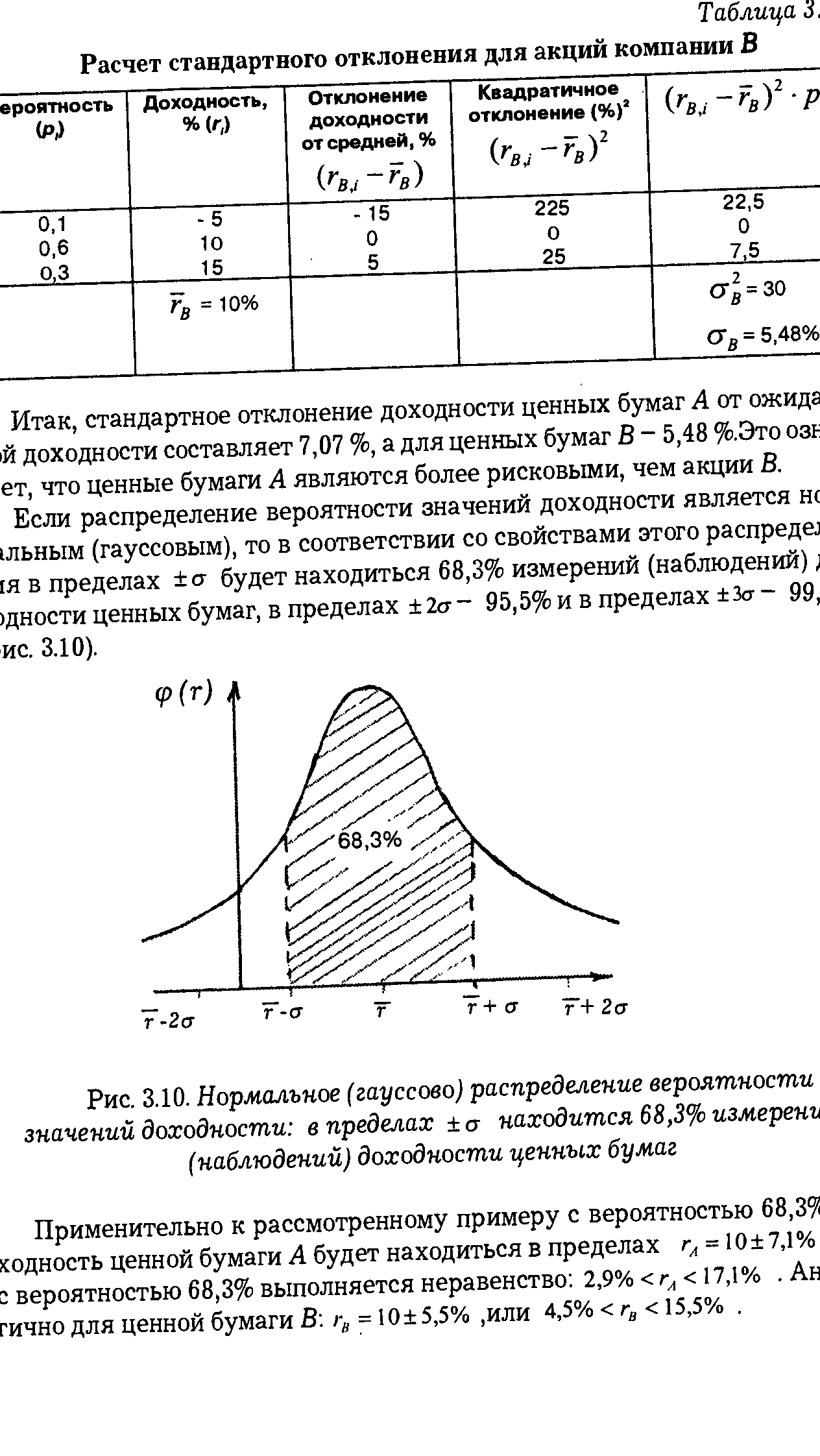 |
Стандартный статистический анализ начинается с выдвижения предположения о том, что изучаемая система является, прежде всего, случайной то есть причинный процесс, создавший временной ряд, имеет много составных частей или степеней свободы, и взаимодействие этих компонентов настолько комплексно, что детерминистичное объяснение невозможно. Только вероятности могут помочь нам понять процесс и использовать его в своих интересах. Лежащая в основе философия подразумевает, что случайность и детерминизм не могут сосуществовать. В Главе 1 мы рассматривали нелинейные стохастические и детерминированные системы, которые представляли собой комбинации случайности и детерминизма, например, игру хаоса. К сожалению, как мы видели в Главе 2, эти системы недостаточно хорошо описываются стандартной гауссовой статистикой. До сих пор мы исследовали эти нелинейные процессы, используя численные эксперименты в зависимости от конкретного случая. Для изучения статистики этих систем и создания более общей аналитической структуры нам нужна теория вероятности, которая является непараметрической. То есть нам нужна статистика, которая не делает предварительных предположений о форме распределения вероятностей, которое мы изучаем. [c.61]
Кроме того, существует возможность того, что результаты вызваны смещением, происходящим в генераторе псевдослучайных чисел, которое не уменьшается при двойном перемешивании. Возможно, объем выборки 300 все еще недостаточен. Для проверки смещения выборки использовался независимый ряд чисел. Этот ряд составляли 500 ежемесячных изменений индекса S P 500, нормализованных к нулевому среднему и единичной дисперсии. Перед началом эксперимента эти числа перемешивались 10 раз. Затем они беспорядочно перемешивались 300 раз, и вычислялись значения R/S, как и прежде. Результаты приведены в таблице 5.2. Они фактически неотличимы от гауссова генерированного ряда. Результаты еще более замечательны, когда мы полагаем, что рыночные прибыли не являются обычно распределенными они имеют толстые хвосты и высокий пик в среднем значении, даже после перемешивания. Судя по этим результатам, мы можем сказать, что в формуле Эниса и Ллойда чего-то не хватает для значений п меньше 20. Чего в ней не хватает - неизвестно. Тем не менее, опытным путем я смог вывести поправку к формуле Эниса и Ллойда. Эта поправка умножает (5.4) и (5.5) с поправочным коэффициентом и дает [c.78]
Черный шум также характеризуется разрывами в проекции прямой времени на ней существуют резкие прерывистые движения вверх и вниз. Эти прерывистые катастрофы приводят к появлению высоких пиков в среднем и толстых хвостов в частотном распределении процессов черного шума. Мандельброт (Mandelbrot, 1972) назвал это свойство эффектом Ноя, памятуя о библейской истории о потопе. На рисунке 13.6 показано частотное распределение изменений для FBM, использованное для создания рисунков 6.6(а) и (Ь). Этот ряд имеет Н = 0,72, согласно R/S-анализу, и его частотное распределение подобно нормальному гауссову шуму. Мы можем видеть (1), что алгоритмы имитации FBM не обязательно охватывают все ожидаемые характеристики, и (2) один большой недостаток R/S-анализа R/S-анализ не может различить дробные гауссовы шумы и дробные негауссовы шумы. Поэтому [c.181]
