При внедрении статистических методов контроля важно установить, какой закономерности подчиняется распределение контролируемых параметров изделий электронной техники (кривой нормального распределения Гаусса распределению, характеризуемому кривой Максвелла, и т. д.). Изменение величины конкретного контролируемого параметра изделия или технологического режима проявляется в изменении функ- [c.159]
Это есть система алгебраических уравнений. Применяя метод исключения Гаусса определяем координаты вектора и0 [c.209]
Инженерные задачи Обращение квадратной матрицы методом Гаусса-Жордана , Матричные вычисления и др. [c.107]
Распределение нормированного отклонения выборочной средней от генеральной средней при численности выборки и —> оо определяется уравнением Лапласа-Гаусса [c.167]
Уравнение Лапласа - Гаусса предполагает непрерывное изменение / и неограниченное возрастание п. Поэтому площадь нормальной кривой, заключенную между ординатами /, и t2, определяют, интегрируя функцию (7.7). [c.168]
Вторая задача специфична для статистических связей, а первая разработана для функциональных связей и является общей. Основным методом решения задачи нахождения параметров уравнения связи является метод наименьших квадратов (МНК), разработанный К. Ф. Гауссом (1777-1855). Он состоит в минимизации суммы квадратов отклонений фактически измеренных значений зависимой переменной у от ее значений, вычисленных по уравнению связи с факторным признаком (многими признаками) х. [c.232]
Несмотря на существенную условность применения в экономическом анализе стохастических моделей, они достаточно распространены, поскольку с их помощью можно прогнозировать динамику основных показателей, разрабатывать научно обоснованные нормативы, идентифицировать наиболее значимые факторы. Многие методы, разработанные в математической статистике, базируются на понятии нормального закона распределения, введенного Карлом Гауссом. Это обусловлено следующими причинами. Во-первых, оказывается, что при экспериментах и наблюдениях многие случайные величины имеют распределения, близкие к нормальному. Во-вторых, даже если распределение некоторой случайной величины не является нормальным, то ее можно преобразовать таким образом, чтобы распределение преобразования, т.е. новой величины, было уже близким к нормальному. В-третьих, нормальное распределение мо- [c.118]
Наибольшее распространение получили величины, распределенные по нормальному закону или закону Гаусса. Плотность распределения такой величины выражается формулой [c.262]
Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами а и а2, если ее плотность вероятности имеет вид [c.34]
Теорема Гаусса— Маркова [c.60]
Доказательство теоремы Гаусса—Маркова в общем виде приведено в 4.4. [c.62]
Теорема Гаусса— Маркова, рассмотренная выше для парной регрессионной модели, оказывается верной и в общем виде для модели (4.2) множественной регрессии [c.87]
Не включая предпосылку 5 — требование нормальности закона распределения вектора возмущений Е, которая в теореме Гаусса—Маркова не требуется. [c.87]
Доказательство теоремы Гаусса— Маркова. Оценка дисперсии возмущений [c.94]
Теперь мы имеем возможность привести доказательство теоремы Гаусса— Маркова, сформулированной в 4.2. [c.94]
Оценки, определяемые вектором (4.8), обладают в соответствии с теоремой Гаусса—Маркова минимальными дисперсиями в классе всех линейных несмещенных оценок, но при наличии мультиколлинеарности эти дисперсии могут оказаться слишком большими, и обращение к соответствующим смещенным оценкам может повысить точность оценивания параметров регрессии. На рис. 5.1 показан случай, когда смещенная оценка Ру, [c.110]
Оценка Ь, определенная по (4.8), хотя и будет состоятельной, но не будет оптимальной в смысле теоремы Гаусса— Маркова. Для получения наиболее эффективной оценки нужно использовать другую оценку, получаемую так называемым обобщенным методом наименьших квадратов. [c.152]
Следовательно, на основании теоремы Гаусса— Маркова наиболее эффективной оценкой в классе всех линейных несмещенных оценок является оценка (4.8), т. е. [c.154]
Напомним также ( 7.1), что оценка Ь (7.16), оставаясь несмещенной и состоятельной, не будет оптимальной в смысле теоремы Гаусса— Маркова, т. е. наиболее эффективной. Это означает, что при небольших выборках мы рискуем получить оценку Ь, существенно отличающуюся от истинного параметра р. [c.157]
Ее фафик — колоколообразная кривая Гаусса, имеющая максимум в точке F= mF, представленная на рис. 10.5. [c.214]
| Рис. 10.5. Кривая нормального распределения Гаусса для значений функций долевого участия собственных средств | 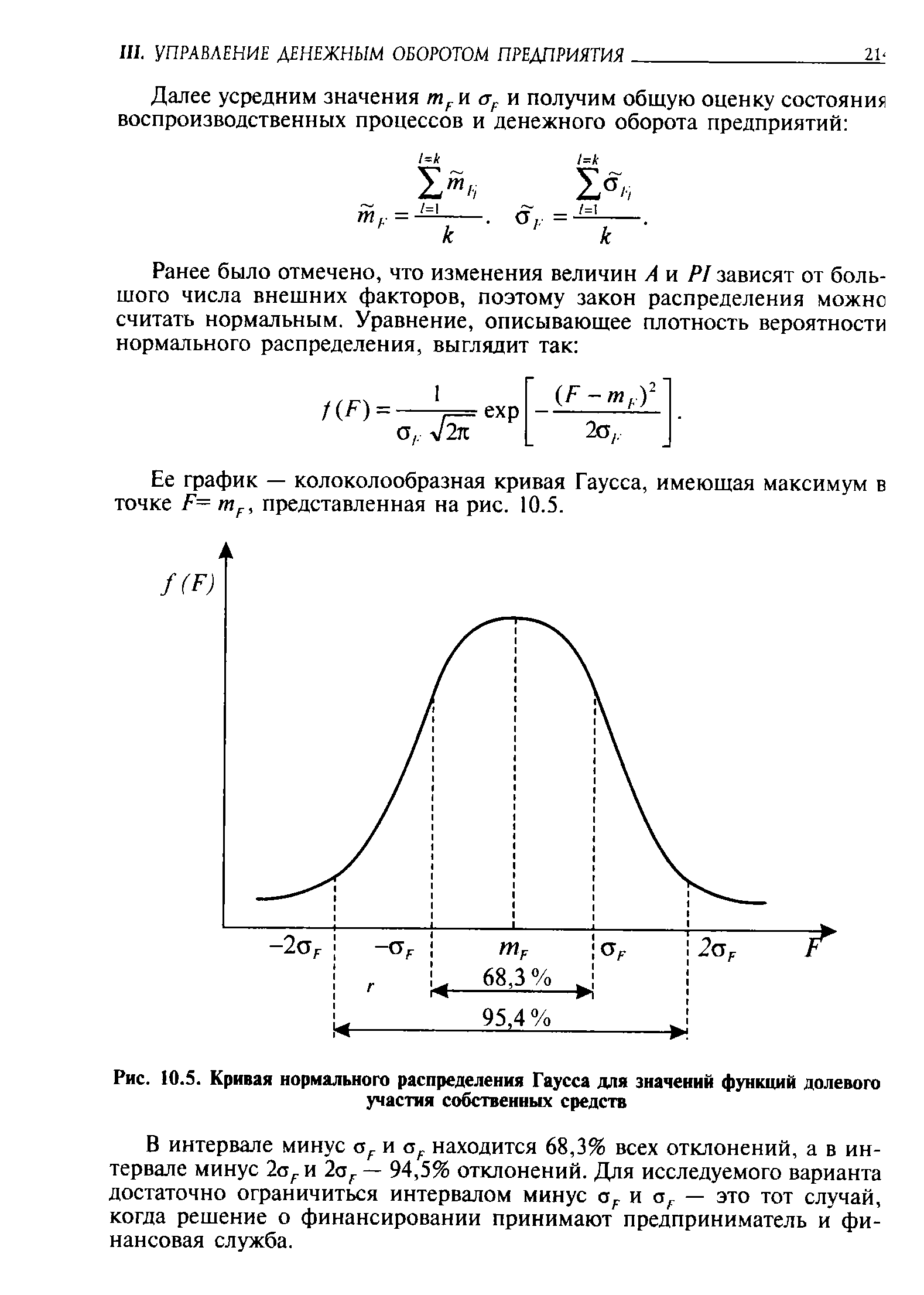 |
Метод Гаусса — это последовательное изменение состава опорного решения до получения оптимального варианта, не допускающего улучшения, это способ решения оптимизационной задачи, у которой оценка и ограничения являются линейными функциями. Рассмотрим алгоритм метода Гаусса на числовом примере. [c.121]
Наиболее распространены статистические методы предупредительного контроля, основывающиеся на законе нормального распределения, характеризующегося известной кривой Гаусса. [c.155]
Наиболее распространенной теоретической кривой, описывающей симметричное распределение, является кривая Гаусса, называемая также нормальной кривой (фиг. 27). Ее уравнение [c.77]
По существу, кривая Гаусса соответствует только симметричным распределениям. Однако она может быть получена и как предельная кривая, к которой стремятся прочие кривые распределения по мере беспредельного возрастания числа независимых обстоятельств, от которых зависят наблюдаемые явления. [c.77]
Сохранение закона Гаусса для описания несимметричных явлений желательно потому, что математические операции [c.77]
Вместо исправления кривой Гаусса можно непосредственно применять несимметричные кривые распределения (Пуассона, Пирсона и др.). [c.78]
Поэтому, чтобы подобрать нормальную кривую Гаусса, необходимо [c.79]
Одним из важнейших распределений, встречающихся в статистике, является нормальное распределение (распределение Гаусса), относящееся к классу экспоненциальных. Плотность вероятности этого распределения [c.34]
Распределение имеет вид симметричной колоколообразной кривой, распространяющейся по всей числовой оси. Распределение Гаусса зависит от двух параметров (//, сг). [c.34]
Плотность вероятности распределения Гаусса нельзя проинтегрировать для получения интегральной функции распределения вероятностей F(x) в явном виде. F(x) можно найти с использованием [c.35]
Распределение Гаусса можно использовать в качестве первого приближения для описания, например, логарифмов относительного изменения цен активов. Однако, только в качестве первого приближения, потому что на практике распределения этих величин отличаются от нормального, то есть имеют как правило более ярко выраженный пик и более "тяжелые" хвосты. Следовательно эти распределения являются островершинными и имеют эксцесс, превышающий три (иногда очень существенно). [c.35]
При ручном способе решения эффективным может оказаться метод квадратных корней и метод последовательного исключения неизвестных (метод Гаусса), при машинном решении — метод последовательных приближений (метод Зейделя) или метод Гаусса. [c.37]
Рассмотрим пример составления корреляционного уравнения линейного тица методом Гаусса. [c.40]
Это позволяет описывать кривой Гаусса и несколько несимметричные опытные кривые, предполагая, что они по мере увеличения числа наблюдений выравниваются. Если отклонения от симметрии значительны, то возможно исправление кривой Гаусса введением так называемой пертурбационной функции, в виде многочлена не выше четвертой степени. Эту же кривую можно представить в виде ряда по производным нормального закона Гаусса (ряд Грамма — Шарлье типа А). [c.77]
Проф. А. Р. Ржаницын рекомендует [47] для несимметричных законов исправлять кривую Гаусса путем преобразования основной шкалы в логарифмическую [c.77]
В нормальной кривой асимметрия и эксцесс равны нулю, а куртозис равен трем. Эти данные могут служить дополнительными признаками соответствия эмпирического материала нормальному закону Гаусса. [c.79]
