Для моделирования случайных величин, подчиненных произвольному закону распределения, заданному функцией распределения у = = F(x), определяют квантиль данного распределения [c.154]
Казалось бы, распределение Коши выглядит очень привлекательно для описания и моделирования случайных величин. Однако в действительности это не так. Свойства распределения Коши резко отличны от свойств распределения Гаусса, Лапласа и других экспоненциальных распределений. [c.39]
Метод Монте-Карло представляет собой расчетный численный способ решения исследовательских задач математического характера на основе моделирования случайных величин и формализованного описания неопределенности. Этот способ, называемый также методом статистических испытаний, на основе статистических данных и различного рода ограничений позволяет сформировать имитационные модели и создать множество сценариев реализации задач исследования и выбрать наиболее вероятный из них. [c.121]
Метод статистических испытаний позволяет воспроизвести любой процесс, на протекание которого влияют случайные факторы, при помощи моделирования случайных величин. Чтобы получить случайную величину, необходимо знать закон ее распределения. При наличии числовых характеристик случайной величины определить закон распределения можно по коэффициенту вариации (отношению среднего квадратического отклонения к среднему значению). В первом приближении выбор закона распределения может быть произведен по табл. 6.3. [c.130]
| Таблица 6.4 Формулы для моделирования случайных величин [65] | ![Таблица 6.4 Формулы для моделирования случайных величин [65]](/pic1/006023146006076023140093060067247216146096064143.png) |
Моделирование случайных величин. Для моделирования случайной величины необходимо знать ее закон распределения. Наиболее общим способом получения последовательности случайных чисел, распределенных по произвольному закону, является способ, в основе которого лежит их формирование из исходной последовательности случайных чисел, распределенных в интервале [0,1] по равномерному закону. [c.121]
Формулы для моделирования случайных величин [c.123]
Закон распределения случайной величины Плотность распределения Формула для моделирования случайной величины [c.123]
Определим продолжительность интервала между отказами th используя формулу для моделирования случайной величины, распределенной в соответствии с экспоненциальным законом [c.125]
Для моделирования случайной величины промежуток [О, 1) разделим участки А( так, чтобы длина промежутка А равнялась Р., = 1, 2,. ... п. Hoi [c.83]
Возможность моделирования случайных величин и процессов очевидным образом может быть использована для моделирования (имитации) реальных явлений, ситуаций, объектов. При этом наблюдение небольшого числа реализаций случайной величины вряд ли принесет нам пользу, но наблюдение большого их числа позволяет сделать правильные выводы об их средних характеристиках. Такой подход лежит в основе метода Монте-Карло, который использует предельные соотношения теории вероятностей законы больших чисел и предельные теоремы. [c.3]
Конспект лекций по курсу Моделирование и управление в экономике предназначен для студентов 4 курса специальности Прикладная математика . Курс читается в течении двух семестров и включает в себя помимо лекционных занятий лабораторные и индивидуальную работу. В структуре курса можно выделить три части первая часть посвящается моделированию случайных величин, векторов и процессов вторая часть посвящена методам моделирования систем массового обслуживания третья часть посвящена собственно теории линейных экономических моделей. [c.3]
Замечание (по поводу термина - метод статистических испытаний (метод Монте-Карло). Мы знаем, то это метод моделирования случайных величин, объектов с последующим использованием статистических характеристик для приближенного решения соответствующей аналитической задачи. Другими словами - численный метод решения аналитических задач. [c.11]
| Рис. 3.3. Схема моделирования случайной величины ,, распределенной по закону Пуассона | 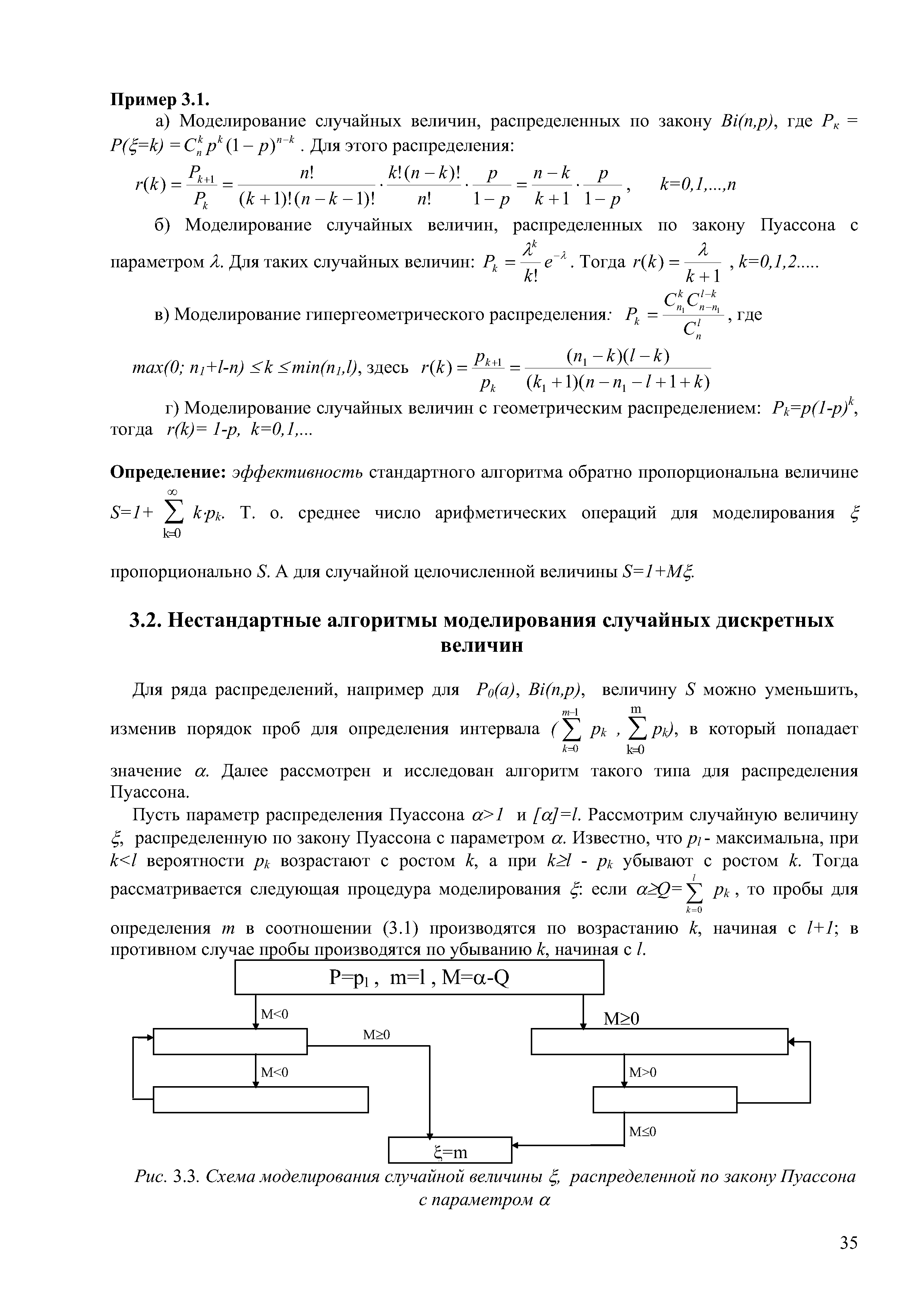 |
Написать алгоритм моделирования случайной величины , имеющей указанную плотность распределения/ ). [c.59]
Написать алгоритм моделирования случайной величины при помощи метода суперпозиции. [c.59]
Написать алгоритм моделирования случайной величины по методу исключения. [c.59]
Моделирование случайной величины—основное содержание метода статистических испытаний. Исходными при моделировании случайных величин являются случайные величины, равномерно распределенные на промежутке 0, 1]. Другие виды распределений получают с помощью специальных методов преобразования такой равномерно распределенной величины. [c.305]
Из требования прибыльности разработки должно выполняться неравенство ZnK > a/ o + Р/Л/СО> которое следует из изложенных предпосылок. Оно определяет допустимые значения и соотношения констант при моделировании. Моделирование заключалось в реализации усеченной нормально распределенной случайной величины (запасов руды) VH с математическим ожиданием V и дисперсией о> и последующим расчетом всех величин, характеризующих отработку . [c.79]
Общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части — объясненную и случайную. Сформулируем задачу моделирования самым общим, неформальным образом на основании экспериментальных данных определить объясненную часть и, рассматривая случайную составляющую как случайную величину, получить (возможно, после некоторых предположений) оценки параметров ее распределения. [c.10]
Метод широко применим не только в эконометрическом моделировании, но и вообще в статистическом исследовании. Так, с его помощью можно оценивать вероятности событий, связанных со случайными величинами. [c.285]
В процессе реализации метода Монте-Карло производится моделирование случайных событий и соответствующих им случайных величин. При таком моделировании определяется, произошло или не произошло в данном испытании некоторое событие А, вероятность которого известна и равна Р(А), и устанавливается, какое значение приняла соответствующая случайная величина X, закон распределения которой известен. С этой целью решают вспомогательную задачу, состоящую в моделировании равномерно распределенной в интервале (0,1) случайной величины со, Пусть, например, известна вероятность некоторого события А [c.154]
Во 2-й главе рассказано о наиболее употребительных законах распределения случайных величин и основных параметрах этих законов. Даны методы поиска функции распределения вероятности случайной величины в случае неинтегрируемой плотности вероятности, а также алгоритмы получения последовательностей случайных величин с произвольным законом распределения, что необходимо при моделировании случайных процессов. [c.10]
В этой главе мы рассмотрим наиболее употребительные законы распределения случайных величин, а также основные параметры этих законов. Будут даны методы поиска функции распределения вероятности случайной величины в случае неинтегрируемой плотности вероятности, а также алгоритмы получения последовательностей случайных величин с произвольным законом распределения, что необходимо при моделировании случайных процессов. Особое внимание будет уделено обобщенному экспоненциальному распределению, которое наиболее пригодно при изучении ценообразования активов. [c.30]
Необходимость в резервном запасе показана на рис. 8.1, где рассматривается реальный случай, когда интенсивность сбыта — случайная величина. Используя фактические данные о сбыте и времени доставки заказа, можно смоделировать процесс и определить, что произойдет при применении правил заказа в течение длительного промежутка времени. Результаты моделирования, выраженные через вероятность дефицита и средние уровни запасов, можно сравнить с результатами, полученными для существующей системы. [c.295]
Для описания неопределенности аварийных рисков применяют различные способы математического моделирования теории вероятностей, лингвистических переменных и нечетких множеств, интервальной математики и статистики, теории игр и т. п. Предположим, что в принятой математической модели неопределенность носит вероятностный характер, а потери описываются одномерной случайной величиной (а не случайным вектором или процессом), т.е. ущерб адекватно описывается одним числом, величина которого зависит от случая. [c.275]
Некоторые авторы работ, посвященных оценке рисков, оптимистические результаты имитационного моделирования объясняют перебором промежуточных вариантов. Здесь можно вспомнить одну из слабых сторон данного метода, рассмотренных выше интервал возможных значений параметра задавался с вероятностью, равной 1, т.е. исключались случаи непопадания случайной величины параметра в определенный интервал. Кроме того, учтенными оказались многие нереалистичные ситуации, которые в модели оказались равновероятными с реальными. Возможно, полученные результаты моделирования в разных границах объясняются именно этими аспектами. [c.48]
Учитывая матричную форму изложения в учебнике вопросов множественной регрессии, в приложении (главе 11) приведены основные сведения из линейной алгебры. Кроме того, в ыаве 12 рассмотрено применение компьютерных пакетов для оценивания эконометрических моделей, а также проведение эксперимента по методу Монте-Карло, основанного на компьютерном моделировании случайных величин. [c.4]
Моделирование случайных величин, распределенных с известными параметрами, по расчетным формулам табл. 6.4 производится с генерированием равномерно распределенных случайных чисел в интервале (0 1) или нормально распределенных случайных чисел , с параметрами среднее — 0, среднее квадратическое отклонение — 1. Если объем моделируемых величин невелик, то для получения случайных чисел и можно воспользоваться специальными таблицами. Получить и Ц можно также с помощью входящей в современное программное обеспечение стандартной процедуры формирования случайных чисел. В частности, производя расчеты в электронных таблицах MS Ex el, необходимо подключить надстройку Пакет анализа , после чего в падающем окне меню Сервис появится команда Анализ данных . В одноименном диалоговом окне необходимо выбрать такой инструмент анализа, как Генерация случайных чисел . [c.132]
Для моделирования случайной величины, распределенной по закону Вейбулла, сначала необходимо вывести на экран столбец случайных чисел, равномерно распределенных в интервале (0 1). Для этого в диалоговом окне Генерация случайных чисел указывается равномерное распределение чисел между 0 и 1. Затем случайные числа подставляются в формулу (см. табл. 6.4) [c.134]
Но моделирование случайных величин, векторов, процессов связанно с применением ЦВМ, а значит и дискретизацией времени ti < ii <. . . < t < Иными словами при цифровом моделировании всегда используются случайные последовательности значений процесса [c.66]
Затем, предположив у случайной величиной, эквивалентной равномерно распределенной на интервале (0,1) случайной величине со, моделировани- [c.154]
Ясно, что моделированием числа со и непосредственной подстановкой в (5.34) получим значения случайной величины, распределенной по закону (5.33). На практике моделирование числа со осуществляют сравнительно простыми средствами, требующими малых затрат машинного времени и позволяющими получать оценки неизвестных параметров с возможно меньшим рассеиванием. При этом сгенерированная последовательность чисел of должна удовлетворять установленным критериям проверки на случайность и периодичность и несущественно отклоняться от равномерного распределения. [c.155]
Моделирование открытия месторождения. Здесь с вероятностью knp имитируется попадание в продуктивную структуру. При отсутствии таковой учитываются затраты, связанные с бурением р поисковых скважин, глубина которых Н есть равномерно распределенная случайная величина от Hmin и Нтах. Если структура продуктивная, то определяется размер z из общей совокупности месторождений, набранных на данной имитации. [c.210]
При оценке совместных вероятностей вы, возможно, захотите смоделировать кривые, образуемые значениями строк и столбцов таблицы, с помощью какого-нибудь математического процесса. Возможно, что при оценке совместных вероятностей или коэффициентов корреляции, введенных совместными распределениями изложенной здесь Теории Условной Вероятности, пригодится какая-нибудь разновидность регрессионного анализа, нейронных сетей или другого аппарата. Это поистине широко открытая область приложений. В главе 4 Математики управления капиталом рассказано о моделировании распределения одной случайной величины с помощью критерия Колмогорова-Смирнова. Этот метод можно также использовать для моделирования строк и столбцов таблицы совместных вероятностей. Тем, кто заинтересован в развитии сходных методов, следует изучить кривые Пирсона, а также Байесову статистику. Для этого рекомендую прочитать Прикладную теорию статистических решений Говарда Райффы и Роберта Шлайфера (изд-во Гарвардского университета, Бостон, 1961 г.) и Адаптивные процессы управления Ричарда Беллмана (изд-во Принстонского университета, Принстон, 1961 г.). [c.168]
Имитационное моделирование (simulation) включает проведение на ЦВМ экспериментов с моделями системы. Применение имитации позволяет сделать выводы о результатах, основанные на вероятностных распределениях случайных величин. Имитационное моделирование позволяет получить оценки степени влияния различных факторов (исходных величин) на зависящие от них результаты (показатели). Результаты имитации дополняются вероятностным и статистическим анализом о степени влияния ключевых факторов на ожидаемые результаты в сценариях развития событий 23. В ТЭО-ИНВЕСТ оценивается степень воздействия случайных факторов на показатели эффективности инвестиций в проект. Вы определяете, какие факторы рассматривать как случайные, указываете допустимый диапазон случайного изменения значений для каждого из них, задаете количество [c.192]
Согласно теореме Муавра — Лапласа биномиальное распределение стремится к нормальному с ростом объема выборки п. Была выдвинута гипотеза о нормальности распределения случайной величины Дх, которая проверялась методом имитационного моделирования. Для проверки гипотезы использовался критерий согласия Колмогорова. [c.58]
