Нестандартные алгоритмы моделирования случайных дискретных величин...........35 [c.34]
Общий метод моделирования случайной дискретной величины основан на очевидном соотношении [c.34]
| Рис. 3.2. Схема моделирования случайных дискретных величин | 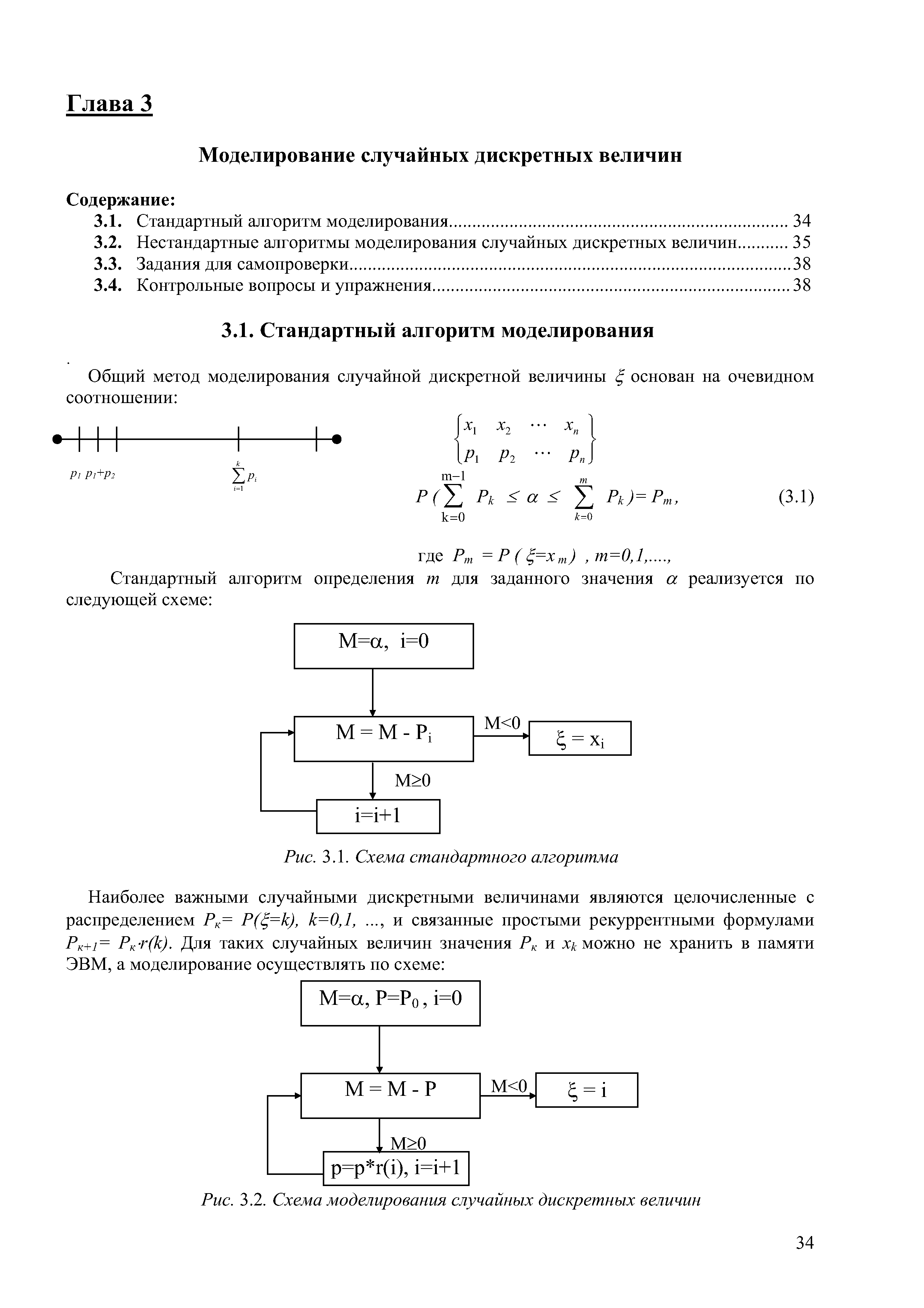 |
Моделирование случайных событий. Моделирование случайного события заключается в воспроизведении факта появления или непоявления случайного события в соответствии с заданной его вероятностью. Моделирование полной группы несовместных событий AI, AI. .... Ап, вероятности которых P(Aj) = Р , i = 1, п известны, можно свести к моделированию дискретной случайной величины Y, имеющей закон распределения [c.125]
Функция вероятности дискретной случайной переменной (или функция плотности вероятности для непрерывных случайных величин) предоставляет информацию о вероятности для переменной принять определенное значение (или в случае непрерывного процесса — информацию о вероятности нахождения в определенном промежутке). Даже если событие, для которого происходит моделирование, произойдет всего один раз, появляется осознание того, что если бы оно было повторено много раз, случайная переменная приняла бы значения, соразмерные с этими вероятностями. [c.410]
Рассмотренная процедура может быть положена в основу выбора направления передачи требований при моделировании замкнутых сетей массового обслуживания. Аналогичным образом можно моделировать дискретные случайные величины при конечном числе их значений. Если имеем дискретную случайную величину у, причем у= 1 с вероятностью Р, а у = 0 с вероятностью 1 — Р, то при имитации ее на ЭВМ необходимо каждый раз решать следующую систему неравенств если 0 < х, < Р, то у,- = 1 если Р < х,- < 1, то у/ = О, где х,- — очередное случайное число от генератора случайных равномерно распределенных чисел. [c.203]
Стандартные алгоритмы моделирования дискретных и целочисленных случайных величин. Трудоёмкость алгоритмов. [c.38]
В основе предлагаемого конспекта лекций лежат лекции, прочитанные на факультете прикладной математики и информатики НГТУ в период с 1995 по 2002 год. В работе содержатся материалы по моделированию дискретных и непрерывных случайных величин, векторов и процессов, по методам моделирования систем массового обслуживания, теории линейных экономических моделей. Конспект предназначен для студентов 4 курса специальности Прикладная математика . [c.2]
Смотреть главы в:
Моделирование и управление в экономике Часть 1 -> Моделирование случайных дискретных величин
