Линейная алгебра лежит в основе методов линейного программирования. С помощью этих методов могут быть решены следующие задачи рассчитана производственная мощность предприятия, цехов, участков разработаны производственные задания цехам, участкам и др. [c.153]
Задачи по оптимизации решаются различными математическими методами, в основе которых лежат теория вероятностей и математическая статистика, линейная алгебра, нелинейное программирование и, в частности, его простейшая форма — квадратичное программирование, а также стохастическое и динамическое программирования и, наконец, матричное исчисление. [c.18]
В связи с широким использованием в настоящее время математических методов и счетно-решающих устройств для планирования и экономических исследований необходимо знание специальных разделов высшей математики — Теории вероятностей , Линейной алгебры , а также основ вычислительной техники. [c.10]
В связи с широким использованием в настоящее время математических методов и счетно-решающих устройств для планирования и экономических исследований, для правильного понимания отдельных разделов курса Экономика нефтеперерабатывающей и нефтехимической промышленности необходимы знания в области высшей математики — теории вероятностей, линейной алгебры, а также основ вычислительной техники. [c.19]
Книга рассчитана на студентов высших учебных заведений, инженеров-экономистов, а также лиц, интересующихся вопросами использования математики в экономических исследованиях и знакомых с основами математического анализа и линейной алгебры. Может быть использована в математических техникумах. [c.2]
Предлагаемая книга предназначена для всех, кто интересуется математической экономикой, знаком с основными понятиями математического анализа, линейной алгебры, теории дифференциальных уравнений и теории вероятностей и хочет получить общее представление о применении математических моделей в экономических исследованиях. Книга в первую очередь предназначена для факультетов переподготовки, где инженеры изучают современные методы управления, но может быть использована и в качестве учебного пособия при обучении студентов технических вузов. [c.13]
Книга рассчитана на студентов вузов, инженеров-экономистов, а также всех, кто интересуется вопросами использования математики и вычислительной техники в экономических исследованиях и знаком с основами математического анализа и линейной алгебры. [c.2]
В форме счетоводства предусматривается составление матричной (шахматной) оборотной ведомости по синтетическим счетам. В программе должно быть предусмотрено использование аппарата линейной алгебры для показа взаимосвязи между отдельными счетами. С этой же целью может быть применен корреляционный анализ. Использование этих методов позволяет получить богатейшую информацию для целей управления. [c.361]
Авторы данного учебника попытались хотя бы в некоторой степени восполнить имеющийся пробел. Учебник написан в соответствии с требованиями Государственного образовательного стандарта по дисциплине Эконометрика для экономических специальностей вузов. При изложении учебного материала предполагается, что читатель владеет основами теории вероятностей, математической статистики и линейной алгебры в объеме курса математики экономического вуза (например, [2] и [12]). [c.3]
Элементы линейной алгебры [c.258]
Аппарат линейной, и в частности, матричной алгебры является необходимым инструментом для компактного и эффективного описания и анализа эконометрических моделей и методов. Ниже (как правило, без доказательств) приводят краткие сведения из линейной алгебры, необходимые для изучения эконометрики. Более подробно с методами линейной алгебры можно познакомиться, например, в пособиях [2], [3]. [c.258]
Головина Л.И. Линейная алгебра и некоторые ее приложения. — М. Наука, 1985. [c.289]
Коэффициенты обычно располагаются в виде прямоугольной таблицы, которая состоит из определенного количества строк и столбцов в зависимости от разнообразия переменных. Схема такой таблицы, называемой в линейной алгебре матрицей, следующая [c.233]
Четвертым методом экономического анализа является математическое моделирование, т. е. построение математических моделей, отражающих внутренние связи между показателями и факторами. С помощью математических моделей удается определить нормативный или расчетный уровень таких важных показателей, как себестоимость, цена, трудоемкость. Математическое моделирование базируется на теории вероятностей, математической статистике, линейной алгебре и других разделах математики, поэтому экономический анализ называют иногда экономико-статистическим. Математические модели (парной или множественной корреляции) не дают точного отражения реального экономического процесса. Формализация зависимостей и связей всегда связана с рядом допущений. Тем не менее точность получаемых с помощью моделей результатов обычно вполне удовлетворительна. Очень часто математические модели изображают в виде номограмм и графиков, которые позволяют наглядно показать зависимости и быстро получить результат, не прибегая к вычислениям. [c.187]
Таким образом, количество входов приходится довольно жестко лимитировать, и выбор наиболее информативных входных переменных представляет важный этап подготовки данных для обучения нейросетей. Глава 4 специально посвящена использованию для этой цели самих нейросетей, обучаемых без учителя. Не стоит, однако, пренебрегать и традиционными, более простыми и зачастую весьма эффективными методами линейной алгебры. [c.134]
Сборник задач по математике для втузов. Ч. 1 Линейная алгебра и основы [c.144]
Беклемишев Д.В. Дополнительные главы линейной алгебры. — М. Наука, 1983. - 336 с. [c.174]
Ильин В. А., Позняк Э. Г. Линейная алгебра. М. Наука, 1978. [c.350]
В.су. в дальнейшем была развита с использованием линейной алгебры и линейного программирования. Основные вопросы при ее исследовании сводятся к трем существует ли решение данной системы уравнений, т. е. возможна ли система цен, количеств товаров и ресурсов, совместных друг с другом единственно ли это решение в том смысле, что для каждой переменной существует только одно значение, совместное с общим решением и наконец, стабильна ли система, способна ли она возвращаться к равновесию при его нарушении [c.40]
ML, транспонированная по отношению к А = [а.] есть М. того же размера, у которой столбцы поменялись местами со строками. Иначе говоря, это [я.1. Обратные и транспонированные М. имеют очень большое применение в моделях МОБ. В них также широко применяется разбиение М. на меньшие подматрицы (блоки). М. коэффициентов систем уравнений — инструмент решения задач математического программирования, задач линейной алгебры и др. [c.187]
При решении многих задач в математике и ее приложениях приходится оперировать многомерными объектами, рассматривать их линейные комбинации и т.п. Методы адекватного описания таких объектов и соотношений между ними были разработаны математиками в рамках векторного и матричного исчисления, а также линейной алгебры. Область применения векторного и матричного исчисления расширилась, когда оказалось, что решение многих нелинейных задач достигается путем линеаризации. Примерами этого могут служить приближенный метод Ньютона для определения корней уравнения, а также линеаризация результатов измерений, первоначально подчиняющихся экспоненциальной или степенной закономерности, с последующей линейной аппроксимацией. [c.47]
Функции, реализующие численные алгоритмы решения задач линейной алгебры [c.52]
При решении задач линейной алгебры необходимость вычислять определитель возникает достаточно часто. Наиболее распространенные приложения определителя — исследование и решение линейных систем. Исследованию линейных систем посвящен специальный раздел. Здесь рассмотрим решение линейных систем по формулам Крамера. Пусть [c.64]
На языке линейной алгебры это значит, что требуется решить систему линейных уравнений (E-A)X=Y относительно неизвестного вектора X при заданной матрице системы Е-А и правой части Y. Если матрица Е-А обратима, то X =(E-A)" Y. [c.72]
Применение стохастических методов к распараллеливанию базовых алгоритмов линейной алгебры [c.156]
Общая характеристика исследования. Было проведено тестирование разработанных стохастических методов на распараллеливании некоторых базовых алгоритмов линейной алгебры [88]. [c.156]
Анализ зависимости распараллеливания алгоритмов линейной алгебры от параметров ВС [c.157]
| Рис. 1.51. Зависимость ускорения S от числа процессоров р для различных алгоритмов линейной алгебры |  |
| Рис. 1.52. Зависимость ускорения S от времени передачи единицы информации по каналам в ВС при распараллеливании некоторых алгоритмов линейной алгебры | 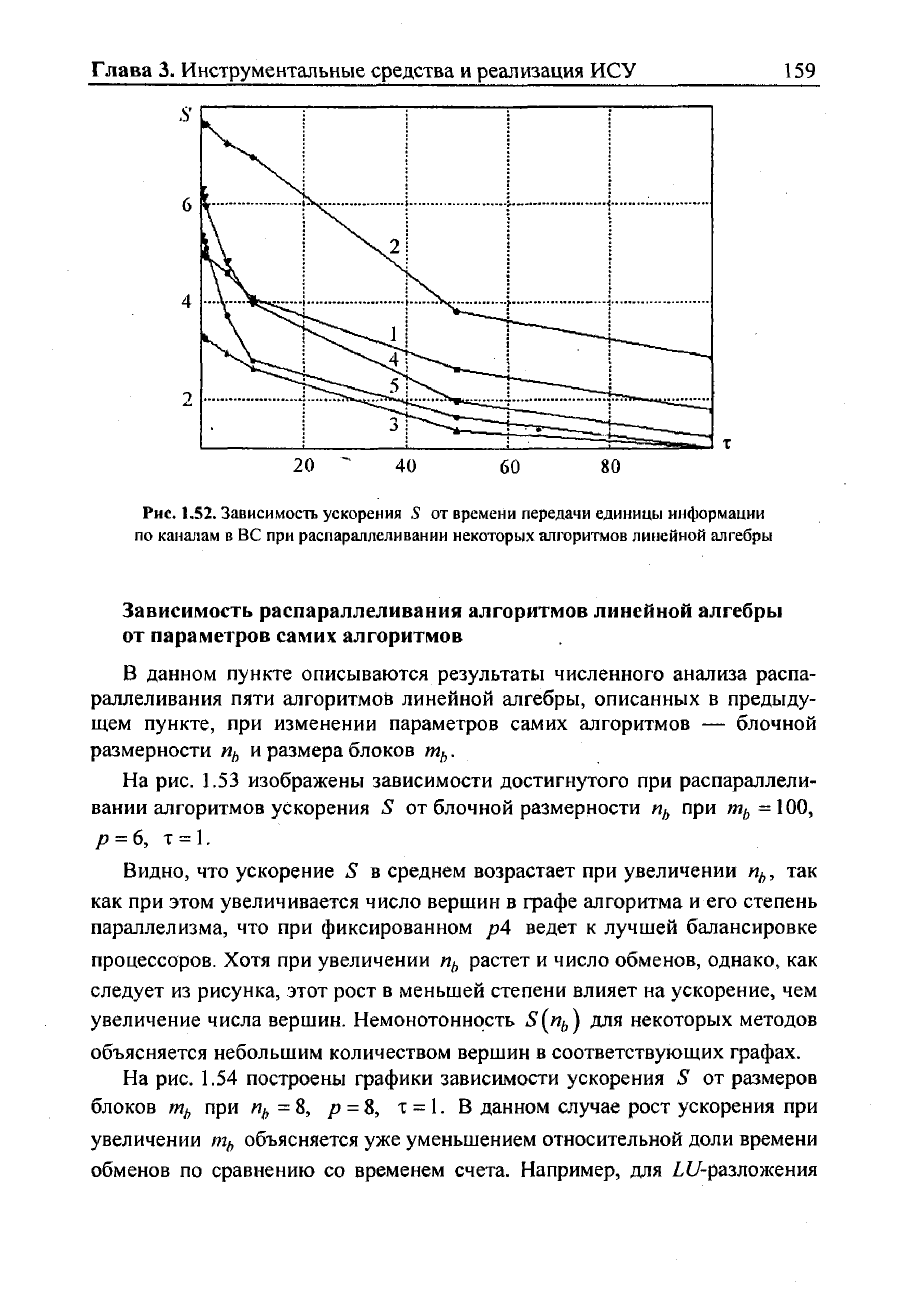 |
В данном пункте описываются результаты численного анализа распараллеливания пяти алгоритмов линейной алгебры, описанных в предыдущем пункте, при изменении параметров самих алгоритмов — блочной размерности пь и размера блоков тъ. [c.159]
Рис, 1.53. Зависимость ускорения S от числа блоков nh для некоторых алгоритмов линейной алгебры [c.160]
Книга, предлагаемая читателю, является учебным пособием такого типа. Она предназначена для всех, кто хочет получить общее представление о методах экономико-математического моделирования и знаком с основными понятиями линейной алгебры, математического анализа, теории дифференциальных уравнений и теории вероятностей. Книга может быть использована при преподавании экономико-математического моделирования в инженерно-экономических высших учебных заведениях,- а также как учебное пособие для студентов младших курсов экономико-математи-%ческих специальностей. Книга может быть использована также на факультетах и курсах переподготовки, на которых специалисты с высшим техническим или. экономическим образованием изучают современные методы управления. [c.11]
Джузеппе Росси (1845—1921) — итальянский бухгалтер, полагал, что учетная информация передается от человека к человеку посредством документов. Обобщающим документом выступает отчетность, которая отражает хозяйственное положение предприятия, сочетая три вида управленческих функций экономические (актив), юридические (пассив) и административные (отчет о финансовом положении). Росси — автор шахматной формы счетоводства, позволяющей фиксировать факты хозяйственной жизни в матрицах, что создает широкие возможности для применения, в целях анализа, линейной алгебры. [c.163]
Учитывая матричную форму изложения в учебнике вопросов множественной регрессии, в приложении (главе 11) приведены основные сведения из линейной алгебры. Кроме того, в ыаве 12 рассмотрено применение компьютерных пакетов для оценивания эконометрических моделей, а также проведение эксперимента по методу Монте-Карло, основанного на компьютерном моделировании случайных величин. [c.4]
Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. — 2-е изд. М.-Л. Физматгиз, 1963. — 734 с. [c.433]
Фактически для расшифровки языка существует огромный аппарат статистики, методов линейной алгебры, различных полуэвристических методов кластер-анализа и т.п. Эти методы можно рассматривать также, как своеобразные языки, каждый из которых по условию имеет ограниченную область применения. [c.245]
ЛИНЕЙНАЯ АЛГЕБРА [linear algebra] — математическая дисциплина, раздел алгебры, содержащий, в частности, теорию линейных уравнений, матриц и определителей, а также теорию векторных (линейных) пространств. [c.168]
Функции, предназначенные для решения задач линейной алгебры, собраны в разделе Векторы и матрицы (Ve tor and Matrix) их можно разделить на три группы функции определения матриц и операции с блоками матриц, функции вычисления различных числовых характеристик матриц и функции, реализующие численные алгоритмы решения задач линейной алгебры. Опишем наиболее часто используемые функции. [c.50]
В настоящем пункте описываются результаты численного исследования отображения графов алгоритмов линейной алгебры на полносвязные однородные графы ВС в зависимости от числа транспьютеров и скорости работы каналов мультитранспьютерной ВС. Для всех вышеуказанных методов зафиксированы следующие параметры пь = 0 и mh <= 100, [c.157]
Рнс, I.S4, Зависимость устарения S от блочной размерности ть для некоторых алгоритмов линейной алгебры [c.160]
При решении некоторых задач в линейной алгебре возникает задача определения собственных чисел и соответствующих им собственных функций, операторов с блочно-трехдиагональной матрицей L. Сложность задачи определяется, как правило, плохой обусловленностью матрицы, когда максимальное и минимальное собственные числа отличаются на несколько порядков. Для решения этой задачи используется метод обратной итерации. [c.161]
С помощью программной системы PARALLAX было проведено численное исследование распараллеливания ряда наиболее распространенных алгоритмов линейной алгебры на различные архитектуры мультитранспьютерных вычислительных систем. Исследована зависимость эффективности выполнения нескольких блочных алгоритмов линейной алгебры на полносвязных топологиях ВС от параметров ВС и параметров алгоритмов. Показано, что поведение полученных численно кривых S(p) (где за S обозначено достигаемое при распараллеливании ускорение) совпадает с поведением ускорения, полученного из расчетов на реальных многопроцессорных ВС, — сначала линейный рост, затем выход на плоский максимум и, наконец, постепенное уменьшение ускорения, что обусловлено возрастающими временными затратами на организацию обменов данными при увеличении числа процессоров. [c.166]
Смотреть страницы где упоминается термин Линейная алгебра
: [c.11] [c.6] [c.33] [c.471] [c.196]Смотреть главы в:
Справочник по математике для экономистов -> Линейная алгебра
