Из таблицы значений функции Лапласа. следует, что [c.153]
Расчет вероятности наступления завершающего события в заданный срок обычно совершенно необходим, когда установленный директивный срок Гд оказывается меньше рассчитанного срока наступления завершающего события Тс. Предполагая, что значение 7"с подчиняется закону нормального распределения, можно рассчитать эту вероятность следующим образом. Аргумент нормальной функции распределения вероятностей (функции Лапласа) [c.235]
Найдя Ф(х) по таблице значений функции Лапласа (табл. 5.1), определяют вероятность наступления завершающего события в заданный срок. Считается что вероятность Рк должна находиться в пределах 0,35 < Рк < 0,65 (рис. 5.4). [c.42]
Функция Лапласа — нечетная, т.е. Ф(— г) = — Ф(—z). [c.59]
Доверительный интервал, доверительная вероятность и риск. Если случайная величина имеет нормальное распределение, то вероятность того, что ее значение появится в интервале (zo) около среднего значения зависит только от величины z, равной отношению отклонения Д от среднего значения и среднеквадратического отклонения z = Л/о. Интервал +Д называют доверительным интервалом, а соответствующую ему вероятность Р(г) — доверительной вероятностью, она равна при нормальном распределении функции Лапласа. Риск выхода за этот интервал R(z) = [1 — [c.59]
| Таблица 6.1 Значения интеграла вероятностей — функции Лапласа | 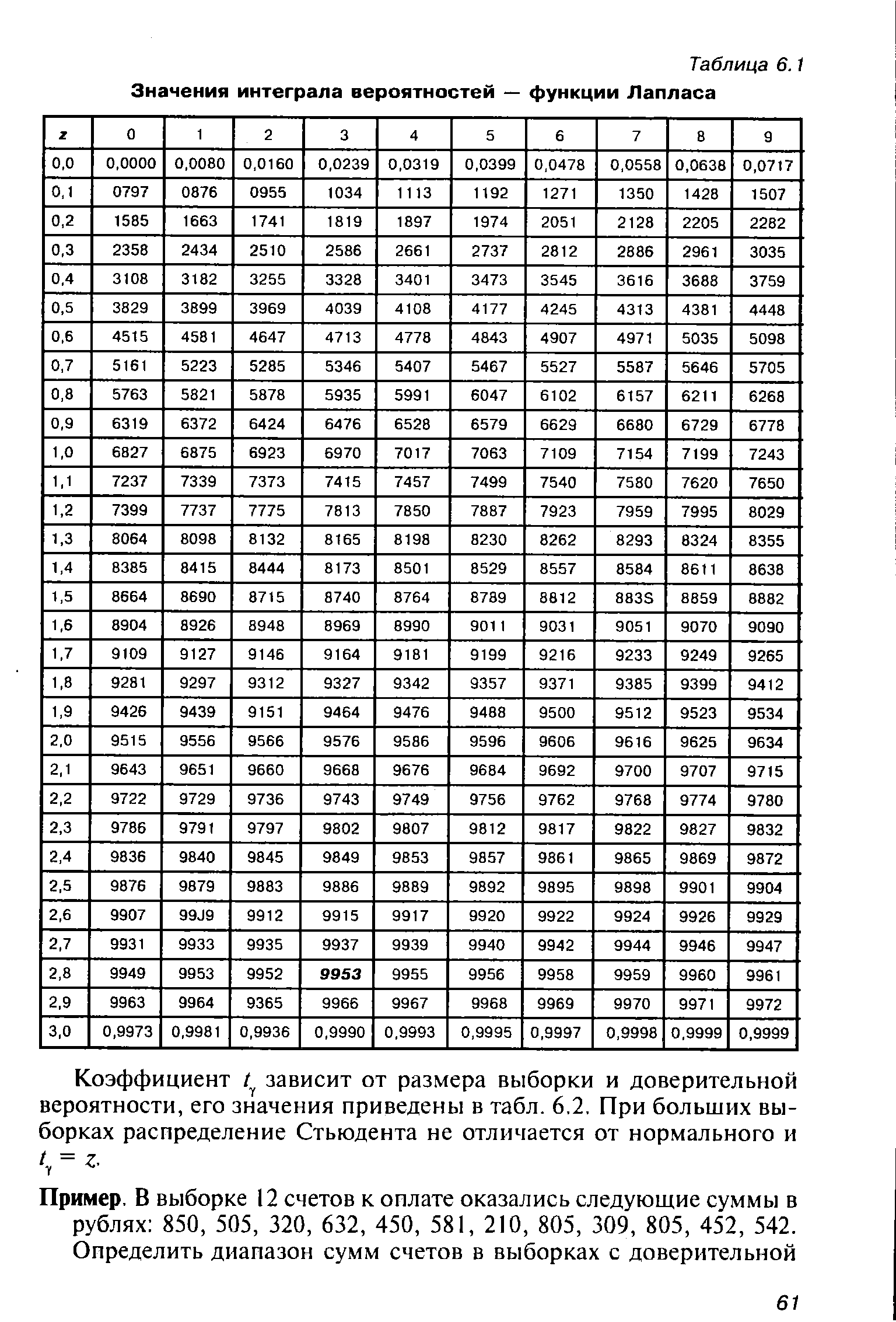 |
Принимаем, что плотность распределения смешанных случайных величин стремится к нормальному закону распределения. Предельную точку кривой нормального распределения выражаем через функцию Лапласа [c.91]
Затем, используя функцию Лапласа, определяют такое-значение А, при котором [c.94]
Ф(х) - функция Лапласа, см. табл. 3.3 1), [c.139]
Функция Лапласа (интеграл вероятностей) [c.139]
Половина интеграла вероятности нормального распределения - функции Лапласа Ф(г) / 2 [c.344]
Подобно функции Лапласа уравнение (2.8) представляет собой квантиль-ное распределение энтропии нормированной нормально распределенной случайной величины на любом отрезке числовой оси. [c.24]
Допустим, произошло смещение центра группирования на величину Дг, тогда t = ta + At, t b=-tb+ ДЛ Используя разложение в ряд Тейлора функции Лапласа Ф(0, получим [c.54]
Эта функция, связанная с интегралом вероятности — функцией Лапласа (см. рис. 27) [c.77]
| Рис. 27. К определению функции Лапласа | 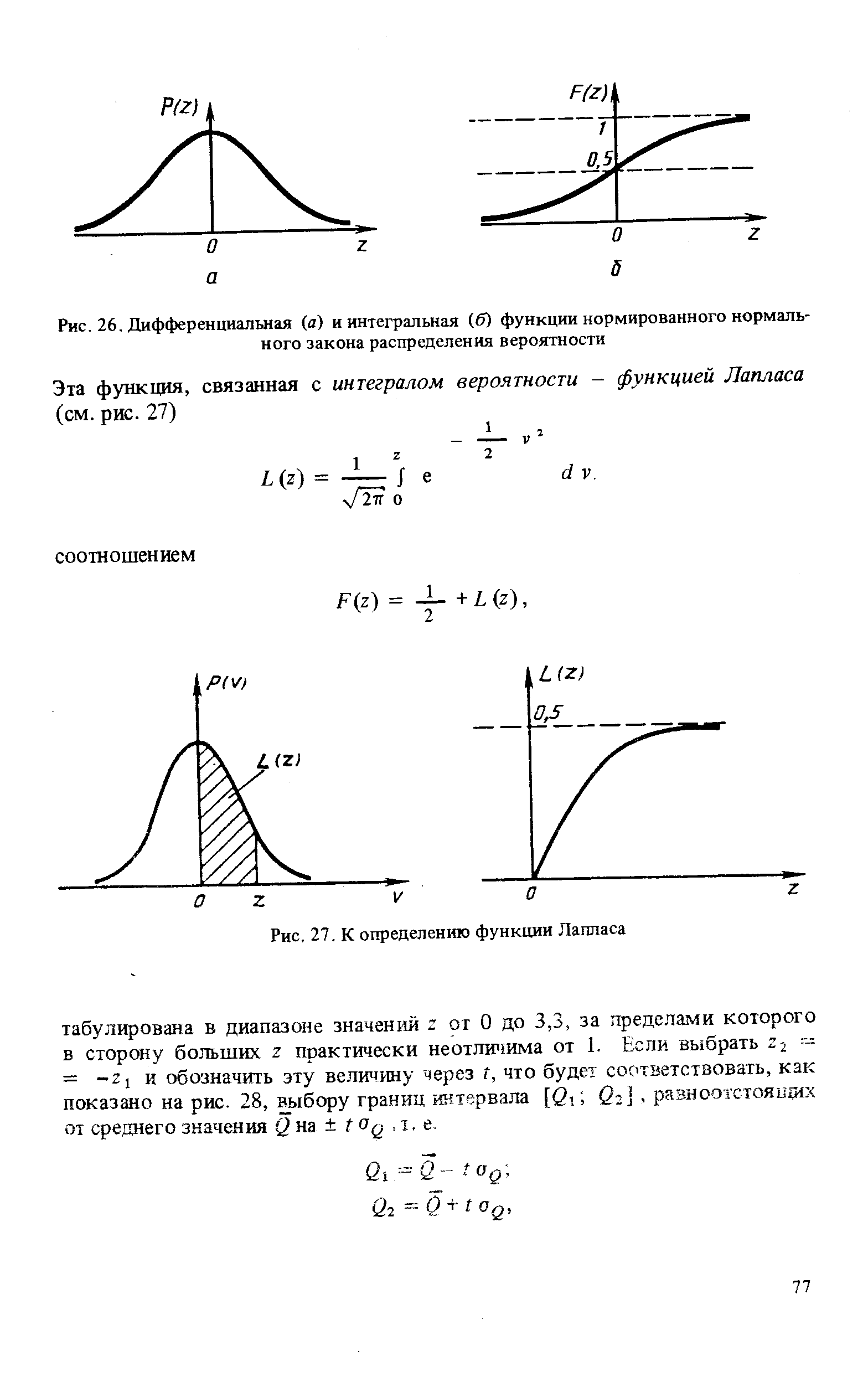 |
Ниже приведены некоторые значения функции Лапласа [Ф( )] для различных коэффициентов (квантилей) f [c.53]
Напомним, Ф (и) = J e " I2 du — нормированная функция Лапласа. [c.156]
Таким образом, если задать величину t и использовать известную функцию Лапласа 0(t), можно определить доверительную вероятность Р = Ф (t), с которой выбор варианта, имеющего более высокую отдачу, будет лучшим (более эффективным). [c.98]
Предельное значение ожидаемой ошибки генеральной совокупности о может быть определено и другим образом — как верхняя граница доверительного интервала. Поскольку известна дисперсия D биномиального распределения, то доверительный интервал ожидаемой ошибки р может быть известным образом выражен через дисперсию и функцию Лапласа. Формула для подсчета доверительного интервала при этом получается громоздкой, но в [11] показано, что для п порядка сотен можно пользоваться удобной для практических расчетов приближенной формулой [c.93]
В. А. Щетина и др., 1988 Тс = <5х<тг/л/п <5— параметр (аргумент) функции Лапласа Ф(<5) а, — среднеквадратическое отклонение интервала между поставками п — максимальное количество поставок в году ретроспективного периода [c.278]
Для практических расчетов специально разработаны таблицы функций f(u), F(u) стандартизированного нормального распределения, однако чаще используется так называемая таблица значений функции Лапласа Ф(и) (Приложение 1). Функция Лапласа имеет вид [c.24]
Нормальное распределение используется при проверке различных гипотез в статистике (о величине математического ожидания при известной дисперсии, о равенстве математических ожиданий и т. д.). Подробная схема работы с таблицей значений функции Лапласа Ф(и) приведена в разделе 1.5.1. [c.26]
В левом столбце таблицы приведены значения СВ U с точностью до десятых, в верхней строке приведены сотые доли U (значения U в данном случае определяются с точностью до сотых). Значение Ф(и) определяется на пересечении соответствующих данному значению и строки и столбца (в данном случае Ф(и) дается с точностью до четвертого знака после запятой). Например, Ф(0.17) = 0.0675, т. е. P(0
Приложение 1 Функция Лапласа (стандартизированное нормальное распределение) [c.335]
По значению t/ из графика на рис. 29 можно опред пить, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, попадает в интервал V100 Uj. С вероятностью в два раза меньшей оно попадает в левую или правую половину этого интервала. Эта вероятность, как показано в разд. 3.3.4, определяется интегралом вероятности - функцией Лапласа L (tj), так что для повышения точности расчетов можно пользоваться не графиком, а таблицами функции Лапласа. Полученные из таблиц значения /. (т/) занесены в пятую графу табл. 11. [c.108]
Критерий Шарлье. Если число результатов наблюдений в ряду велико, то по теореме Бернулли число результатов, превышающих по абсолютному значению Кш И (х) будет и [ 1 — Ф (Кш)], где Ф (Кш) - значение нормированной функции Лапласа для Z — Кш. [c.77]
При проведении статистического анализа весьма часто использу ется таблица значений функции Лапласа (приложение 1) [c.30]
Пусть в качестве альтернативной рассматривается гипотеза H[ m Ф m0. Тогда критические точки иа/2 и Ui a/2 = -ua/2 будут определяться по таблице функций Лапласа (приложение 1) из ус- [c.76]
При H М(Х) M(Y) по таблице функции Лапласа (прило- [c.81]
