МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ [c.38]
Если между экономическими явлениями отсутствует линейная зависимость, то в этом случае могут быть использованы методы динамического программирования. Динамическое программирование позволяет определять границы зон оптимальности при разработке планов повышения эффективности работы предприятий, территориальных и трубопроводных управлений, а также сложных газопроводных и нефтепроводных систем, взаимосвязанных между собой. [c.80]
Методы динамического программирования применяются при решении оптимизационных задач, в которых целевая функция или ограничения, или же первое и второе одновременно характеризуются нелинейными зависимостями. Признаками нелинейности является, в частности, наличие переменных, у которых показатель степени отличается от единицы, а также наличие переменной в показателе степени, под корнем, под знаком логарифма. [c.168]
Решение. Данная задача может быть решена методом динамического программирования. Обозначим gi (x) — прирост выпуска продукции на г-м предприятии при х единиц [c.113]
Специфика этой задачи такова, что для ее решения удобно использовать метод динамического программирования. Не останавливаясь на изложении математических методов, укажем, что в рассматриваемой задаче между отдельными средствами регулирования распределяются две величины — годовой ресурс природного газа и интенсивность газопотребления (условия а, б). Оптимальное распределение этих двух величин (QM. ч, V) методом динамического программирования возможно лишь вследствие условия ( ), позволившего условие (в) свести к относи тельно простой проверке принадлежности точки (Х , г/г-) к области допустимых решений. [c.347]
Обобщая сказанное выше, отметим, что решение задачи сводится к построению графика газопотребления и стоимостных функций fi(xi, г/г). Эта информация является необходимой и достаточной, для того чтобы с помощью метода динамического программирования были вычислены оптимальные значения величин xi, xz,. . ., хп г/i, г/2,. ..,уп. [c.347]
Однако упомянутый выше метод динамического программирования в силу своей специфики дает решение первой из рассматриваемых задач для всех возможных значений величин V и QM. ч- Добавление к оптимальному решению каждой задачи приведенных затрат на магистральный газопровод и сравнение общих затрат даст возможность выбрать оптимальный вариант. [c.348]
Мы можем здесь воспользоваться приближенным решением этой же задачи, полученным с помощью метода динамического программирования (см. ниже в данном параграфе). [c.98]
Расчеты существенно сокращаются и упрощаются при наличии исходного плана, близкого к оптимальному. Поэтому рекомендуется в качестве такого плана брать приближенный результат решения подобной задачи, выполненной методами динамического программирования. [c.100]
Динамическое программирование (планирование) служит для выбора наилучшего плана выполнения многоэтапных действий. Для многоэтапных действий характерно протекание во времени. Кроме действий, естественно носящих многоэтапный характер (например, перспективное планирование), в ряде задач прибегают к искусственному расчленению на этапы, с тем чтобы сделать возможным применение метода динамического программирования. [c.104]
Реализуем метод динамического программирования в со- [c.23]
| Рис. 5. Метод динамического программирования | 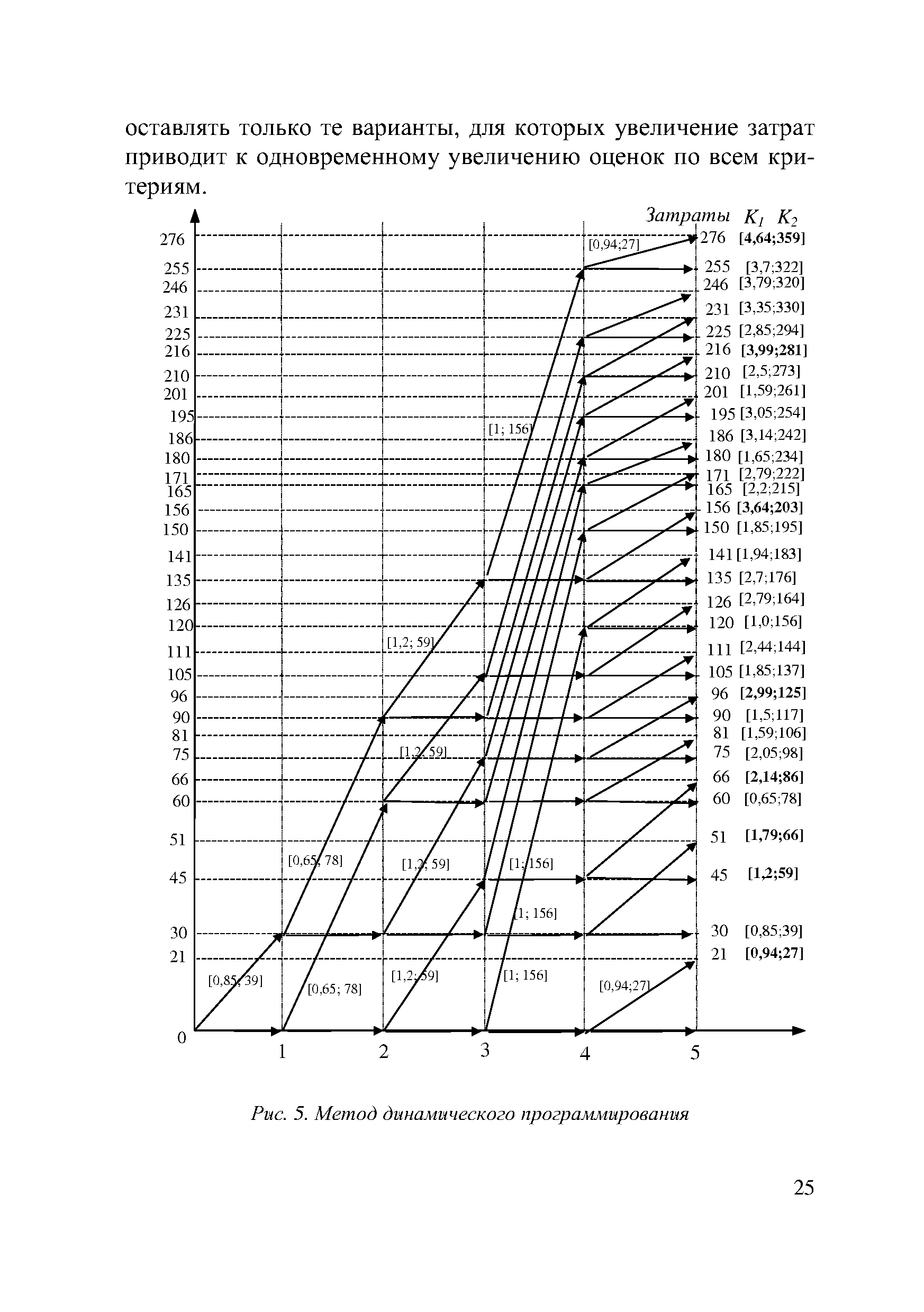 |
В случае дискретных задач метод динамического программирования [c.50]
Метод динамического программирования можно представить в дру- [c.51]
Метод динамического программирования является эффективным ме- [c.52]
Метод динамического программирования, как уже отмечалось выше, [c.53]
Если в методе динамического программирования решением задачи [c.57]
Будем строить математическую модель, для решения которой используется метод динамического программирования. В основе метода динамического программирования лежит принцип Беллмана, формулирующийся следующим образом управление на каждом шаге надо выбирать так, чтобы опти- [c.270]
В первом случае сравниваются затраты на приобретение нового оборудования с издержками эксплуатации действующего и находится оптимальный момент замены. Для решения некоторых из таких задач применимы методы динамического программирования. [c.100]
Использование в экономическом анализе метода динамического программирования покажем на простейшем примере1. [c.168]
Особенность метода динамического программирования заключается в том, что благодаря принципу вложения появляется возможность получения оптимального решения не только для VrnJ1, но также в диапазоне от 0 до VrnJI. Это позволяет на основе численного решения делать соответствующие обобщения, приближая его к аналитическому. [c.149]
Строгое математическое решение поставленной проблемы требует применения достаточно сложного метода динамического программирования, который в данном случае приводит к так называемому алгоритму Вагнера - Уитина. [c.199]
Этот результат может быть получен автоматически при применении так называемого алгоритма Вагнера-Уитина (WW), основанного на методе динамического программирования. Однако при внимательном взгляде на результат нашей эвристической стратегии "Оптим-3" также можно легко заметить, что такое изменение приведет к уменьшению издержек. [c.289]
Смотреть страницы где упоминается термин Методы динамического программирования
: [c.98] [c.148] [c.11] [c.38] [c.14] [c.20] [c.24] [c.48] [c.9] [c.11] [c.3] [c.53] [c.57] [c.19] [c.157] [c.61] [c.61] [c.14] [c.15] [c.15]Смотреть главы в:
Теория экономического анализа -> Методы динамического программирования
