Теорема 4.2. Пусть Х и У — произвольные множества, а функция f(x, и) вогнуто-выпуклая на XxY. Если для любого [c.215]
Лебедев В. Н. Вогнуто-выпуклые задачи стохастического программирования в условиях неопределенности. Изв. АН СССР, Техническая кибернетика , 1969, № 1, с. 9—15. [c.387]
Подобным же образом изменяется предельный продукт любого ресурса. Убывание предельного продукта иллюстрирует рис. 6, на котором представлен график производственной функции в предположении, что только один фактор является переменным. Зависимость объема продукта от затрат ресурса выражается вогнутой (выпуклой вверх) функцией. [c.52]
При нормировании работ по опиливанию деталей из другого материала или вогнутых (выпуклых) поверхностей, или с иной точностью обработки к нормативам, приведенным в табл. 44, применяют коэффициенты. Размеры коэффициентов составляют при обработке [c.193]
Любая стационарная точка дифференцируемой вогнутой (выпуклой) функции f(M) является точкой локального максимума (минимума) этой функции. [c.147]
Оговорка об упрощенности предложенной схемы касается главным образом последнего пункта, а именно формы линий эластичности. В действительности взаимосвязь спроса с ценой обычно далеко не столь однозначна. Как правило, в разных диапазонах изменения цены она варьируется. Следовательно, эластичность должна была бы принять графическую форму выпуклых или вогнутых кривых, а возможно, и ломаных линий, но скорее всего сочетать все эти элементы в какой-то более сложной конфигурации. Однако чисто условно-иллюстративный характер схемы позволяет абстрагироваться от подобной конкретики, которая, что важно подчеркнуть, не влияет на направление общих выводов. (По этому поводу см. также [300, с. 121, 123, 125]. Здесь автор внес коррективы в предложенную статьей методику количественного анализа, которая к тому же, на наш взгляд, обосновывает во многом иные выводы, если последовательно придерживаться по крайней мере формальной логики.) [c.206]
Если же для некоторой функции выполнено обратное условие, то ее называют вогнутой (или выпуклой вверх). Пример выпуклой функции приведен па рис. 1.4, а вогнутой — на рис. 1.5. Можно показать, что в том случае, когда все функции gp(x) (р = 1,. .., пг) выпуклы, множество X также выпукло ). Понятие выпуклости функций и множеств играет важную роль в экономико-математическом моделировании, поскольку позволяет получить интересные качественные результаты. [c.34]
Индивидуальный спрос - спрос индивидуального покупателя. Если сравнить кривые спроса индивидуального покупателя (СИ) с фиксированным доходом и совокупного спроса массы покупателей с разными уровнями дохода (СС), то они будут существенно различаться первая будет выпуклой, а вторая - вогнутой (рис. 1.4). [c.20]
Кривая совокупного предложения является выпуклой при фиксированной номинальной заработной плате, потому что график производственной функции вогнут. В свою очередь, это вытекает из закона убывающей предельной отдачи. Последовательное повышение цен стимулирует увеличение спроса на труд и рост уровня занятости. Но последовательное повышение уровня занятости приводит к уменьшению прироста реального объема производства. [c.565]
Если хотя бы одна из этих функций — нелинейная или содержит произведения искомых переменных, то соответствующая задача — это задача нелинейного программирования. Среди них наиболее изучены задачи выпуклого программирования, в результате решения которых определяют минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве. [c.104]
В координатах х, у для прямоугольника допустимых значений искомых неизвестных строятся линии равной выгодности. Для участника А это совокупность параллельных выпуклых функций, для участника В — это совокупность параллельных вогнутых функций. Точки возможных условий контракта — это точки касания функций полезности результата для участников. [c.114]
При убывающей отдаче от масштаба затраты будут расти в большей мере, чем выпуск, то есть для удвоения объема выпуска потребуется более чем вдвое увеличить количество применяемых ресурсов (рис. 5.1, д). Поэтому кривая LT будет вогнута или выпукла вниз (рис. 5.1, е). [c.88]
Задача (3.120) —(3.123) является задачей выпуклого программирования с вогнутой целевой функцией и линейной системой ограничений. [c.85]
Нормальный спад . При высоких ценах сбывается принципиально меньше товаров, чем при низких. Это относится как к линейным, так и нелинейным зависимостям класса выпукло-вогнутых убывающих функций (в отношении результативного признака), как это показано на рис. 8.3. [c.150]
Примечания 1. При опиливании с проверкой плоскостности и перпендикулярности по линейке и угольнику время, указанное в таблице, надо увеличивать на 10%, а при проверке точности размеров микрометром — на 40%. При опиливании выпуклых и вогнутых поверхностей по шаблонам время обработки увеличивается на 30%. [c.324]
Отметьте, что на хвостах распределения находятся пробелы, т.е. области, или ячейки, где нет эмпирических данных. Эти области сглаживаются, когда мы приспосабливаем наше регулируемое распределение к данным, и именно эти сглаженные области вызывают различие между параметрическим и эмпирическим оптимальным Почему же наше характеристическое распределение при всех возможностях регулировки его формы не очень хорошо приближено к фактическому распределению Причина состоит в том, что наблюдаемое распределение имеет слишком много точек перегиба. Параболу можно направить ветвями вверх или вниз. Однако вдоль всей параболы направление вогнутости или выпуклости не изменяется. В точке перегиба направление вогнутости изменяется. Парабола имеет 0 точек перегиба, [c.135]
Если смотреть на график из начала координат, нисходящая кривая может быть либо вогнутой, либо выпуклой. Наклон вогнутой кривой увеличивается (становится все круче) по мире продвижения вниз по кривой, тогда как наклон выпуклой кривой уменьшается (становится все более пологим). (Вспомните, что кривая производственных возможностей на рис. 2-1 (гл. 2) является вогнутой, что отражает закон возрастающих альтернативных издержек.) Заметим, что на рис. 2 кривая безразличия выпукла по отношению к началу координат. Значит, наклон кривой уменьшается, или становится более пологим по мере продвижения от точки у к точкам k, l, т и так далее вниз вдоль кривой. Пользуясь специальной терминологией, скажем, что наклон кривой безразличия отражает предельную норму замещения (ПНЗ), поскольку показывает, в какой сте- [c.471]
Вновь обратившись к табл. 22-1, вы можете удостовериться в том, что кривая средних переменных издержек имеет форму вогнутой дуги. Предположим, что цена труда составляет, скажем, 10 дол. за единицу. Разделив величину среднего продукта (производительность одного рабочего) на 10 дол. (оплату труда одного рабочего), вы получите трудовые издержки на единицу продукта. Поскольку в нашем примере мы исходили из того, что труд является единственным переменным ресурсом, постольку трудовые издержки на единицу продукта равнозначны переменным издержкам в расчете на единицу продукта, то есть средним переменным издержкам. Изначально, когда величина среднего продукта мала, средние переменные издержки высоки. По мере увеличения количества занятых рабочих средний продукт растет, а средние переменные издержки соответственно сокращаются. Когда средний продукт достигает своей максимальной величины, средние переменные издержки становятся минимальными. Затем, поскольку в производство вовлекается все большее число рабочих, средний продукт начинает сокращаться, а средние переменные издержки расти. Выпуклая кривая среднего продукта представляет собой перевернутую вогнутую дугообразную кривую средних переменных издержек. Заглянув немного вперед, на рис. 22-6, вы найдете этому графическое подтверждение. [c.486]
Кроме того, можно показать, что для азартного инвестора эти кривые безразличия будут вогнуты, т.е. их угол наклона убывает при движении справа налево. Основное объяснение выпуклости вытекает из теории полезности, см. примечания 5 и 7. [c.193]
Кроме того, в гл. 7 установлено, что кривые безразличия для инвестора, избегающего риск, выпуклы и имеют положительный наклон. Теперь мы покажем, что эффективное множество в общем случае вогнуто и имеет положительный наклон, т.е. отрезок, соединяющий любые две точки эффективного множества, лежит ниже данного множества. Это свойство эффективных множеств является очень важным, так как оно означает, что существует только одна точка касания эффективного множества и кривых безразличия. [c.198]
Соотношение цена — доходность для типичной облигации выпукло (открыто вверх), как показано на рис. 16.2. Профессиональные инвесторы часто описывают соотношение цена — доходность для вторичных бумаг, обеспеченных залогом имущества, как вогнутое соотношение, т.е. его график является открытым вниз. Какие свойства этих бумаг являются причиной вогнутости графика [c.478]
Заметим, что если fj(Ui) - вогнутая функция, то YJ - выпуклое множество. В [c.36]
| Рис. 4. Выпуклость, линейность и вогнутость | 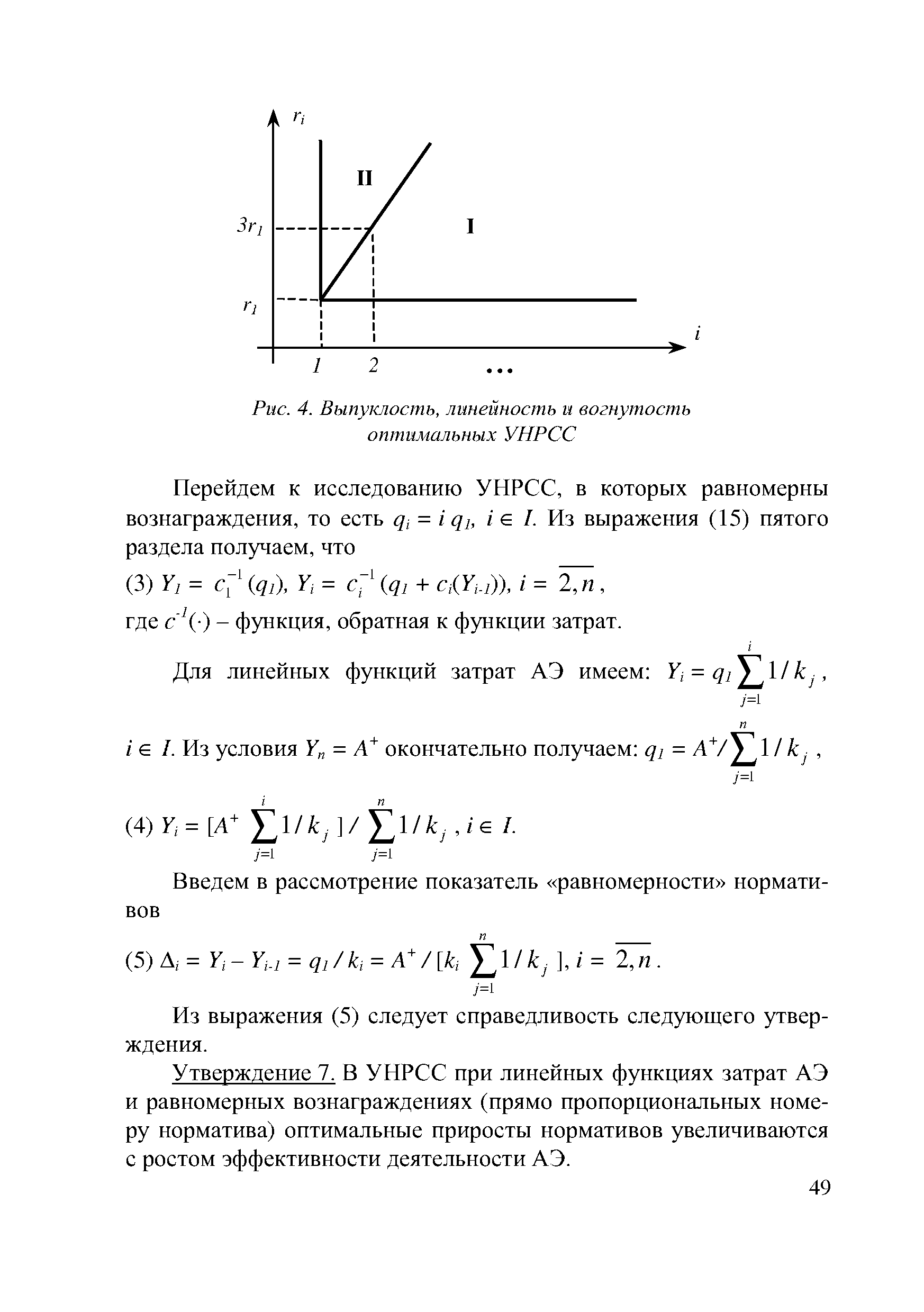 |
Математически это требование формулируется следующим образом / (х) — вогнутая (выпуклая вверх) функция своих аргументов на неотрицательном ортанте. Напомним, что функция называется вогнутой на множестве X, если для любых двух точек (векторов) xt и л 2 из множества X и любого числа а е [О, 1] справедливо неравенство [c.93]
Часто вместо условия (2.13) формулируется более сильное математическое требование, близкое к (2.13). по смыслу f(x) — вогнутая (выпуклая вверх) функция своих аргументов на неотрицательном ортанте, т. е. для любых двух неотрицательных векторов х и х и любого числа a tO, 11 справедливо неравенство [c.73]
Ясно, что каждая вогнутая функция квазивогнута, выпуклая — квазивыпукла, а вогнуто-выпуклая — квазивогнуто-выпукла. [c.214]
Теорема 4.3. [279]. Пусть X(Y) выпукло и компактно, Y(X) — произвольное выпуклое множество, a f(x, у) — вогнуто-выпуклая функция на XxY. Если f(x, у) полунепрерывна сверху по х для каждого г/еУ (полунепрерывна снизу по х для каждого у Х), то имеет место (4.1). [c.215]
Характеристики могут иметь вогнутую, выпуклую или прямолинейную форму и при одном виде продукции могут быть представлены в виде [c.180]
Если f(M) — вогнутая (выпуклая) функция на множестве V, то в любой точке условного локального максимума (минимума) она достигает своего наибольшего (наименьшего) значения. [c.147]
Логистическая кривая имеет форму латинской буквы s положенной на бок, отчего еще называется эсобраэной кривой. Она имеет два перегиба от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста посреди периода к замедляющемуся (выпуклость). Она подходит для отображения развития в течение длительного периода, проходящего все фазы, например процесса насыщения потребителей каким-то новым товаром, скажем, телевизорами сначала медленный, но все ускоряющийся рост доли семей, [c.325]
Если А, > 1, то платежная функция в нуле имеет непрерывную и равную нулю производную, каждая ее ветвь в окрестности нуля выпукла, а затем после точки перегиба и до бесконечности - вогнута. Такая функция больше напоминает платежную функцию комбинации двух стрэнглов, одного длинного и одного короткого. При этом страйки обоих стрэнглов расположены симметрично относительно нуля, а страйки длинного стрэнгла ближе к нулю, чем страйки короткого. Эти платежные функции свойственны более расположенным к риску инвесторам. [c.17]
