Если используется единственный ресурс, а функция f(x) достаточно гладкая, то требования (2.13), (2.14) и (2.15) равносильны. Если же ресурсов несколько, то (2.13) не эквивалентно (2.14) или (2.15), т. е. не эквивалентно вогнутости функции /(х). Легко построить соответствующие примеры. Рассмотрим, например, степенную производственную функцию с двумя ресурсами х и х2. [c.74]
Если хотя бы одна из этих функций — нелинейная или содержит произведения искомых переменных, то соответствующая задача — это задача нелинейного программирования. Среди них наиболее изучены задачи выпуклого программирования, в результате решения которых определяют минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве. [c.104]
В координатах х, у для прямоугольника допустимых значений искомых неизвестных строятся линии равной выгодности. Для участника А это совокупность параллельных выпуклых функций, для участника В — это совокупность параллельных вогнутых функций. Точки возможных условий контракта — это точки касания функций полезности результата для участников. [c.114]
Нетрудно убедиться в строгой вогнутости функции ф(у) при 0<у<1, точка экстремума и экстремальное значение которых соответственно равны [c.151]
Пусть fj - вогнутые функции. В этом случае, как доказано В.Н. [c.17]
Функция S(x) является вогнутой функцией х. Как известно, [c.43]
Из свойств вогнутых функций следует, что достаточным для выполнения (7) [c.120]
Применение вогнутых функций штрафа за корректировку имеет свои минусы. [c.185]
Пусть зависимости fi(Uj) являются вогнутыми функциями количества [c.29]
Заметим, что если fj(Ui) - вогнутая функция, то YJ - выпуклое множество. В [c.36]
Если v(-) - строго монотонная вогнутая функция, то (га, га) - [c.61]
Определим характеристики минимальной вогнутой функции [c.122]
Для любой вогнутой функции справедливо свойство [42]. [c.114]
Для вогнутых функций зона сбалансированности будет шире, од- [c.116]
Вогнутые функции стимулирования. [c.79]
| Рис. 29. Линеаризация вогнутой функции | 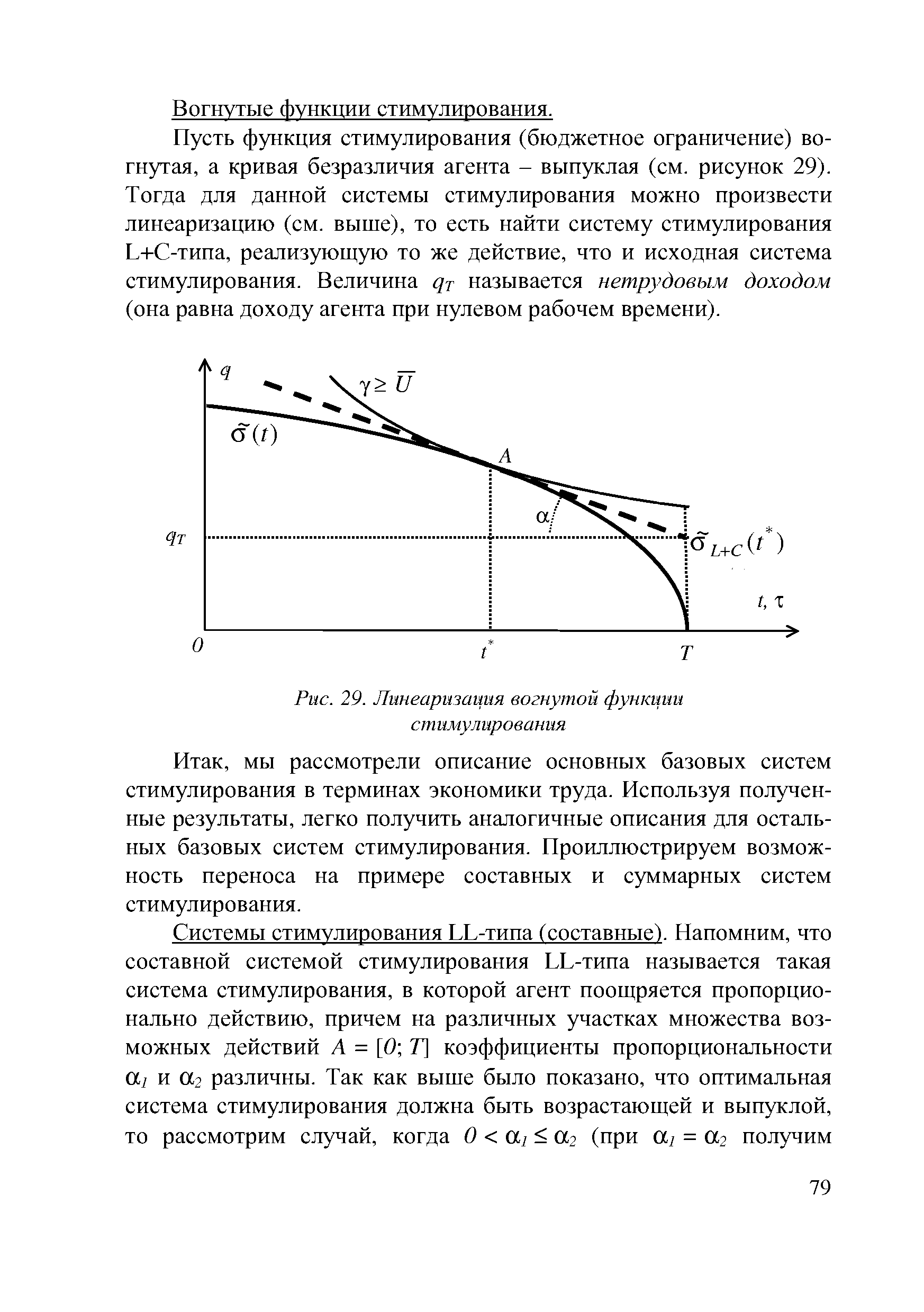 |
