Рассмотрим вопрос об условиях, достаточных для того, чтобы множество допустимых значений X, описываемое соотношениями (3.8), было выпуклым. Этот вопрос решается на основе введения понятия выпуклой функции. Функция g(x), где х е Еп,- называется выпуклой вниз (или просто выпуклой), если для любых значений х и ж и при любом числе ос, изменяющемся от нуля до единицы, выполнено неравенство [c.34]
Если же для некоторой функции выполнено обратное условие, то ее называют вогнутой (или выпуклой вверх). Пример выпуклой функции приведен па рис. 1.4, а вогнутой — на рис. 1.5. Можно показать, что в том случае, когда все функции gp(x) (р = 1,. .., пг) выпуклы, множество X также выпукло ). Понятие выпуклости функций и множеств играет важную роль в экономико-математическом моделировании, поскольку позволяет получить интересные качественные результаты. [c.34]
Свойства выпуклых функций изложены, например, в [67]. 34 [c.34]
Вершины сетевого графика 192 Выпуклые функции 34 [c.391]
Нахождение оптимального варианта возможно для линейной зависимости или выпуклой функции 5,- 3-= =f(ti-j), которая методом кусочно-линейной аппроксимации сводится к решению линейной задачи. [c.117]
В координатах х, у для прямоугольника допустимых значений искомых неизвестных строятся линии равной выгодности. Для участника А это совокупность параллельных выпуклых функций, для участника В — это совокупность параллельных вогнутых функций. Точки возможных условий контракта — это точки касания функций полезности результата для участников. [c.114]
Модель (4.20) — (4.22), (4.25) является статической энтропийной моделью ЗОК. Она представляет собой (ввиду выпуклости каждого слагаемого и в связи с известной теоремой [56] о выпуклости функции, равной сумме выпуклых функций) задачу выпуклого программирования с ограничениями транспортного типа. [c.119]
В (5.5) А, Ь, с - приближенные значения, соответственно, матрицы А, векторов b и с, а Х° — точка, по отношению к которой строится нормальное решение. Кроме того, необходимо отметить, что вместо регулирующей добавки Х — Х° 2 может быть использована любая другая строго выпуклая функция. Так, в работе [88] показан пример использо- [c.145]
Действительно, в случае выпуклой функции издержек удельные издержки при росте значений Dub увеличиваются. [c.90]
Причина, по которой сумма превышает S1 млн. США, связана со свойством выпуклости функции, рассмотренным выше. [c.482]
Метод измерения выпуклости функции содержится в работе [c.484]
Некоторые исследования, критически оценивающие использование понятий среднего срока, выпуклости функции и иммунизации, упоминаются в примечании 18. Другие критические исследования включают [c.485]
| Рис. 31 Ожидаемый успех как выпуклая функция от стоимости хеджирования | 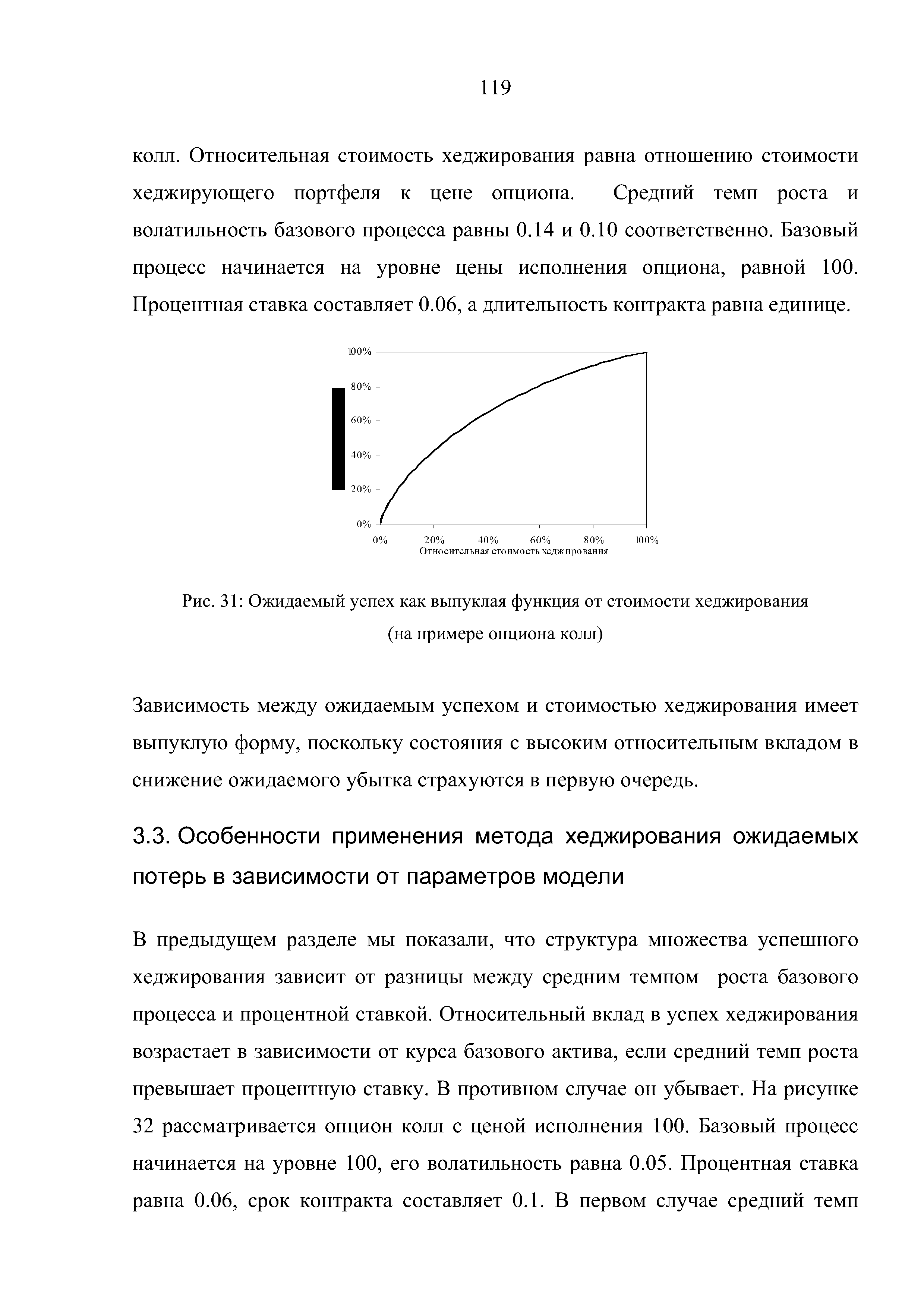 |
При использовании выпуклых функций штрафа за корректировку следует [c.185]
Действительно, боясь большого штрафа за корректировку (при выпуклых функциях [c.185]
Выпуклые функции приоритета. Пусть ЛДУ ) = У и У [c.15]
Можно показать, что R-механизм с выпуклыми функциями [c.15]
Пусть (Y) кусочно-линейная выпуклая функция Y с точками [c.18]
Из свойств выпуклых функций [42] [c.88]
Из выпуклости функции ф() следует, что иь ок - 1 [c.90]
С (Лтг), где С (-) - монотонная выпуклая функция, d(0) = 0, i e /. [c.146]
Для района в целом также имеет место выпуклость функции "затраты — выпуск". Но она обусловлена также и необходимостью перехода на экономически менее эффективные объекты разработки в целях получения дополнительной добычи. И для отрасли в целом эта функция выпукла вниз, что обусловлено еще одним фактором — фактором географической отдаленности. Для получения новых мощностей по добыче отрасль вынуждена переносить фронт работ во все более отдаленные и необустроенные районы. Здесь уже имеет место нелинейность экстенсификации. Таким юбразом, на всех трех уровнях прослеживается рост удельных ных вложений в новые мощности с увеличением [c.68]
Таким образом, при выпуклых функциях затрат агента эффек- [c.53]
Смотреть страницы где упоминается термин Выпуклые функции
: [c.67] [c.229] [c.484] [c.57] [c.132] [c.54] [c.14] [c.38] [c.117] [c.120] [c.38] [c.55] [c.31] [c.53] [c.56] [c.39] [c.43] [c.56] [c.86] [c.90] [c.148] [c.164] [c.164] [c.24] [c.67]Смотреть главы в:
Вариационные принципы механики сплошной среды -> Выпуклые функции
Экономико-математический словарь Изд.5 (2003) -- [ c.57 ]
Матричное дифференциальное исчисление с приложениями к статистике и эконометрике (2002) -- [ c.0 ]
50 лекций по микроэкономике Том 2 (2000) -- [ c.2 , c.569 , c.572 , c.573 , c.574 , c.620 , c.622 , c.632 , c.644 , c.645 , c.655 , c.674 ]
