Первое личико — это рисунок первого утверждения теоремы. Если глаза личика блестят (+ +), то оно улыбается. Значит, если знак второй производной плюс, то функция выпукла вниз. [c.162]
Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх. [c.162]
| Рис. 8. Функции выпуклая вниз (а), выпуклая вверх (б), не имеющая постоянного знака выпуклости (в). | 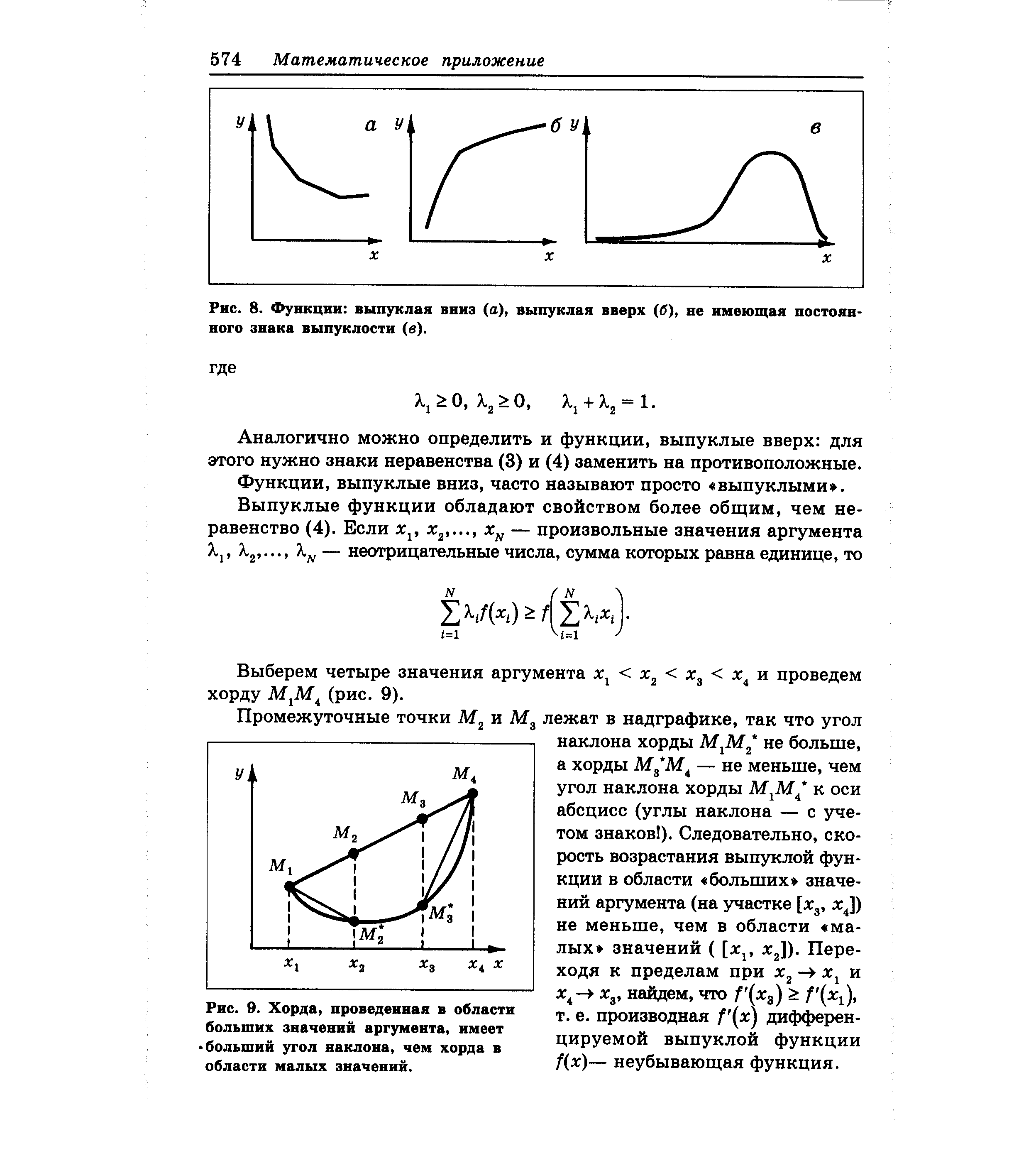 |
Существуют ли функции, выпуклые вниз и выпуклые вверх одновременно [c.575]
Функции, выпуклые вниз, часто называют просто "выпуклыми". [c.187]
Для случая л>2 приведённые определения функции выпуклой вниз и выпуклой вверх переписываются с незначительными корректировками. [c.104]
Рассмотрим вопрос об условиях, достаточных для того, чтобы множество допустимых значений X, описываемое соотношениями (3.8), было выпуклым. Этот вопрос решается на основе введения понятия выпуклой функции. Функция g(x), где х е Еп,- называется выпуклой вниз (или просто выпуклой), если для любых значений х и ж и при любом числе ос, изменяющемся от нуля до единицы, выполнено неравенство [c.34]
Специфика задачи оптимизации транспортировки нефти проявилась также в выборе критерия оптимальности. В качестве последнего принят минимум расхода энергозатрат — важнейшей составляющей себестоимости, зависящей от объема перекачки. Поскольку эта зависимость нелинейна, то в модели задачи целевая функция нелинейна, в частности, кусочно-линейна, выпукла вниз. [c.72]
Из формулы для выражения средних издержек fT(y) через количество поставок п(Т) видно, что средние издержки являются выпуклой вниз функцией, т. е. достигают минимума в т. Q0, соответствующей оптимальному количеству поставок п(Т) так как ближайшими значениями к Q0 из допустимых целых являются Q и Q2, то минимум достигается в одной из этих точек, что треб, доказать. [c.14]
Теорема 4.1. Если функция распределения F(t) имеет непрерывную первую производную, то кривая Лоренца выпукла вниз, т. е. у" > 0 (условие выпуклости вниз) [c.101]
Математически формулируется достаточное условие выпуклости графика непрерывной функции y=f(x), определенной на интервале (а, Ъ) (которая в этом случае предполагается дважды дифференцируемой функцией) если она имеет отрицательную вторую производную, то ее график является выпуклым вверх, если положительную — выпуклым вниз. Точка графика непрерывной функции, при переходе через которую график меняет направление выпуклости (напр., был выпуклым вверх, стал — вниз), называется точкой перегиба. [c.58]
Если
Если функция L в (2.167) при всех значениях Л выпукла вниз по W, то базовое значение единственно если, наконец, множество Dw — Du x Dz можно разбить на несколько подмножеств, число которых М° меньше m + 1 и на каждом из которых L выпукла вниз, то число базовых решений не превосходит числа М°. Справедливость этого утверждения следует из (2.167). [c.95]
Решение единственно, если функция Лагранжа L выпукла вниз по //, т.е. если [c.105]
Требование минимума <т по w в силу выпуклости вниз этой функции [c.110]
Условие выпуклости вниз функции единственность решения , имеет вид [c.173]
Оно заведомо выполнено, если выпукла вниз функция [c.173]
Для большинства реальных законов массопереноса задача (5.70), (5.71) выпукла вниз по у, и ее решение соответствует условию стационарности функции Лагранжа [c.192]
Условие (6.15) показывает ограничения на объемы перекачки, в том числе сверху — на пропускную способность соответствующего участка нефтепровода. Формула (6.16) выражает для каждой вершины сети баланс между суммарным поступлением нефти извне системы и от других вершин сети- и суммарным потреблением, включая собственно потребление в самой вершине и перекачку нефти к другим вершинам сети и вне системы. Целевая функция (6.17)—критерий минимизации суммарных энергозатрат перекачки по всей системе. Функции frs(xrs) — кусочно-линейные и выпуклые (вниз). Каждая из них соответствует минимально возможным энергозатратам на перекачку различных объемов нефти по отдельным участкам системы. Строятся функции frs(XrS) по методу огибающей, т. е. находится нижняя граница выпуклой оболочки точек, характеризующих фиксированные режимы работы соответствующих насосных агрегатов и их комбинаций [26]. [c.156]
График дифференцируемой функции у = f(x] называется выпуклым вниз в данном промежутке, если соответствующая часть графика расположена выше касательной, проведенной в любой точке промежутка. [c.160]
Последнее неравенство означает, что график функции у = = /(ж) лежит выше касательной. Следовательно, в промежутке X график функции будет выпуклым вниз. [c.161]
Необходимое условие выпуклости слабее если функция выпукла в промежутке X, то можно утверждать лишь, что f"(x 0 (или f"(x 0), х 6 X. Например, функция у — х выпукла вниз на всей числовой оси, хотя вторая производная у" = = 13 х2 не всюду положительна /"(0) = 0 при х = 0. [c.162]
Заметим, что для непрерывных функций, которые являются дифференцируемыми не во всех точках, также используется понятие выпуклости кривой. Оно возникает, например, в математическом программировании. Здесь не может быть использовано наше определение, использующее понятие касательной (касательной в этом случае может и не быть). Поэтому пользуются другим определением, основанном на понятии хорды. График функции (или сама функция) называется выпуклым (выпуклой) вниз, если каждая дуга кривой лежит не выше своей хорды. График функции (или сама функция) называется выпуклым (выпуклой) вверх, если каждая дуга кривой лежит не ниже своей хорды. [c.164]
Точка х = 0 разбивает числовую ось на интервалы (—сю, 0) и (0, +оо). В первом интервале вторая производная отрицательна, а во втором — положительна. Следовательно, в первом интервале график функции является выпуклым вверх, а во втором — выпуклым вниз. При этом вторая производная при переходе через точку х — О меняет знак. Это означает, что значение х — О является абсциссой точки перегиба графика. Вычислим ординату этой точки /(0) = 0. Таким образом, точка 0(0, 0) — точка перегиба графика заданной функции. [c.176]
Вторая производная не обращается в нуль и не определена лишь в точке разрыва ж = 4. Поскольку точка перегиба должна быть точкой графика функции, то график функции точек перегиба не имеет. Остается выяснить вопрос об интервалах выпуклости функции. В интервале (—оо, 4) вторая производная отрицательна, кривая выпукла вверх. В интервале (4, +оо) вторая производная положительна, кривая выпукла вниз. [c.179]
Что означают эти неравенства Напомним, что если вторая производная положительна, то график функции одной переменной является выпуклым вниз, а если вторая производная отрицательна, то график направлен выпуклостью вверх. Знак второй производной величины показывает рост или убывание предельной величины. Если вторая производная производственной функции (одной переменной) положительна, то эффективность ресурса растет, если отрицательна, эффективность падает. [c.344]
Целевой функционал Q(x, у) стохастической транспортной задачи— выпуклая вниз функция переменных yj. Действительно, [c.36]
При естественном предположении q( - - q +)5г 0 имеем f, (yj) 0. А это означает, что fo(yi), а вместе с ней и Q(x, у) — выпуклые вниз функции yj. [c.36]
Пусть распределение Рь(Б) — компонент случайного вектора в задаче с вероятностными ограничениями — приводит к эквивалентной задаче выпуклого программирования. Тогда и распределение Fb[h(B)], где h(S) — неотрицательная выпуклая вниз возрастающая функция, не равная тождественно постоянной, сводит стохастическую задачу к эквивалентной детерминированной задаче выпуклого программирования. [c.74]
Показатели качества решения и ограничения детерминированных эквивалентов стохастических задач часто определяются средними штрафами за невязки условий. Приведем достаточные условия, при которых математическое ожидание штрафа за невязки у=Ах — b условий — выпуклая вниз функция параметров управления х. [c.81]
Теорема 6.1. Для того чтобы f(x) была выпуклой вниз функцией х, достаточно, чтобы для каждого t (i=l,. .., т) удовлетворялось одно из следующих двух условий [c.82]
Чтобы доказать, что f(x) выпукла вниз, достаточно убедиться в том, что для любого i, i=l,. . ., т, функция [c.82]
Таким образом, условия (а) оказываются достаточными для выпуклости вниз функции / (х). [c.82]
Равенство (5.4) является также и достаточным условием, поскольку функция Q(x) выпукла вниз. [c.163]
Пусть требуется минимизировать выпуклую вниз функцию ср(л ) на выпуклом множестве К. [c.181]
Для района в целом также имеет место выпуклость функции "затраты — выпуск". Но она обусловлена также и необходимостью перехода на экономически менее эффективные объекты разработки в целях получения дополнительной добычи. И для отрасли в целом эта функция выпукла вниз, что обусловлено еще одним фактором — фактором географической отдаленности. Для получения новых мощностей по добыче отрасль вынуждена переносить фронт работ во все более отдаленные и необустроенные районы. Здесь уже имеет место нелинейность экстенсификации. Таким юбразом, на всех трех уровнях прослеживается рост удельных ных вложений в новые мощности с увеличением [c.68]
Функция Лагранжа для этой задачи с условиями (5.19), как легко показать, выпукла вниз по д , 02 и достигает минимума в единственной точке. Это значит, что оптимальные значения потоков 0 и 02 постоянны и определяются выражениями (5.19). Однако законы перемещения поршней, естественно, отличаются от тех, которые соответствуют соотношениям Онзагера (5.27). [c.174]
ПРОГРАММИРОВАНИЕ ВЫПУКЛОЕ ( onvex programming) — раздел программирования математического, целевая функция и системы ограничений являются выпуклыми В П в локальный и глобальный экстремумы совпадают Задача П в сводится к отысканию минимума выпуклой вниз ф-ции Ею могут быть, напр, издержки производства [c.202]
Во-вторых, специфика зависимости величины минимума расхода электроэнергии на перекачку от ее объема (в соответствии с принципом 1 это и отображено в критерии оптимальности) такова, что эта зависимость выражается кусочно-линейной выпуклой (вниз) функцией. Это позволило построить точный, быстро сходящийся алгоритм решения задачи, являющейся обобщением метода потенциалов решения сетевой транспортной задачи линейного программирования (СТЗ ЛП) для случая кусочно-линейного выпуклого функционала [41, 47]. Для построения экономико-математической модели задачи введем обозначения г — номер вершины сети 3 (г, s) —дуга сети между вершинами г и s R(E) — множество вершин (дуг) сети Rir(R r< R) [R2t(R2r z zR) подмножество вершин сети, из которых выходят дуги, входящие в r-ю вершину (в которые входят дуги, выходящие из г-й вершины) ur(vr) — объем поступления (потребления) нефти в r-й вершине за плановый период . х — объем перекачки нефти по дуге (г, s) за плановый период ars(Prs) — нижний (верхний) предел значений xrs frs(xrs) — функция зависимости расхода электроэнергии от объема перекачки для дуги (г, s). [c.156]
При а05гО,5 k представляет собой ( в силу положительной определенности формы Zj ijXiXj] выпуклую вниз функцию х. Таким образом, при еде- [c.68]
Согласно теореме 3.5 3 гл. 1 S(a) выпуклая вниз функция. Если выполнено условие невырожденности, то 5 (а) определена в окрестности сю и, значит, непрерывна в точке о, т. е. S(ao) =-5 (ао). Поэтому [c.89]
