Другой математической записью данной задачи, эквивалентной по результату, является ее постановка в виде модели выпуклого программирования (функции ср, выпуклые). [c.199]
Для изучения влияния факторов на результаты хозяйствования и подсчета резервов в анализе применяются такие способы, как цепные подстановки, абсолютные и относительные разницы, интегральный метод, корреляционный, компонентный, методы линейного, выпуклого программирования, [c.38]
В упомянутых ситуациях предполагается, что зависимости между параметрами модели имеют линейный характер, что сохраняется и с течением времени. В принципе такая предпосылка весьма условна, поэтому в теории принятия решений разработаны также методы нелинейного, динамического, стохастического, выпуклого программирования, которые гораздо более сложны и в анализе деятельности отдельных предприятий применяются крайне редко. [c.141]
Если хотя бы одна из этих функций — нелинейная или содержит произведения искомых переменных, то соответствующая задача — это задача нелинейного программирования. Среди них наиболее изучены задачи выпуклого программирования, в результате решения которых определяют минимум выпуклой (или максимум вогнутой) функции, заданной на выпуклом замкнутом множестве. [c.104]
Из задач выпуклого программирования подробно разработаны задачи квадратичного программирования, в которых требуется найти максимум (или минимум) квадратичной функции при условии, что ее переменные удовлетворяют некоторой системе линейных уравнений. [c.104]
Рассматриваемая стохастическая задача при этом преобразуется в детерминированную задачу выпуклого программирования с линейной целевой функцией и квадратичными ограничениями. [c.69]
Утверждение 3.2. Задача (3.98) -(3.1 00), (3.104) является задачей выпуклого программирования. [c.80]
Таким образом, приближенный детерминированный аналог многоэтапной стохастической задачи (3.92) -(3.96) при сделанных допущениях оказывается задачей выпуклого программирования, решение которой может быть осуществлено известными методами [46, 56]. [c.84]
Задача (3.120) —(3.123) является задачей выпуклого программирования с вогнутой целевой функцией и линейной системой ограничений. [c.85]
Модель (4.20) — (4.22), (4.25) является статической энтропийной моделью ЗОК. Она представляет собой (ввиду выпуклости каждого слагаемого и в связи с известной теоремой [56] о выпуклости функции, равной сумме выпуклых функций) задачу выпуклого программирования с ограничениями транспортного типа. [c.119]
Так как задача (4.29) — (4.31) является задачей выпуклого программирования, то к ней может быть применен любой из известных алгоритмов решения. Однако специальный тип ограничений обусловил возможность [c.125]
Прежде чем переходить к его описанию, рассмотрим результаты работы [94], имеющие непосредственное отношение к рассматриваемой проблеме. Изложение будем вести в обозначениях работы [94]. Рассмотрим задачу выпуклого программирования [c.133]
Наряду с (4.64) рассмотрим задачу выпуклого программирования с линейными ограничениями [c.133]
Задача планирования для НПП в детерминированной или вероятностной постановке сводится к решению задачи линейного или выпуклого программирования, причем задачи стохастического программирования, характерные для НПП, как показано в работе [47], преобразуется в эквивалентную задачу линейного программирования, которая имеет вид [c.205]
Во всех рассмотренных нами случаях мы полагали, что зависимости между факторами линейные и характер их не меняется со временем. Это далеко не всегда бывает так, поэтому в теории принятия решений используются также методы нелинейного, динамического, стохастического, выпуклого программирования, которые гораздо более сложны и применяются в анализе деятельности отдельных предприятий крайне редко. [c.111]
Графики и диаграммы незаменимы для иллюстрации результатов экономико-математических методов, которые находят все более широкое применение в экономическом анализе. К ним относятся корреляционный и регрессионный анализ, линейное, динамическое и выпуклое программирование, теории игр и теории массового обслуживания, матричные методы, эвристические методы и др. Об этом более подробно — в следующей главе. [c.72]
Для разработки наилучших стандартпланов работы поточных линий и предметных участков используются различные современные математические методы линейное и выпуклое программирование, метод ветвей и границ и "различные приближенные методы. [c.4]
Согласно теореме 1 это задача выпуклого программирования. [c.36]
Процедурная сторона анализа существенно усложняется ввиду множественности вариантов, техника прямого счета в этом случае практически не применима. Наиболее удобный вычислительный аппарат — методы оптимального программирования (линейное, нелинейное, динамическое, выпуклое программирование и др.) — достаточно хорошо разработан в теории, однако на практике в экономических исследованиях относительную известность получило линейное программирование. [c.555]
| Рис. В.4. Задачи вогнутого и выпуклого программирования | 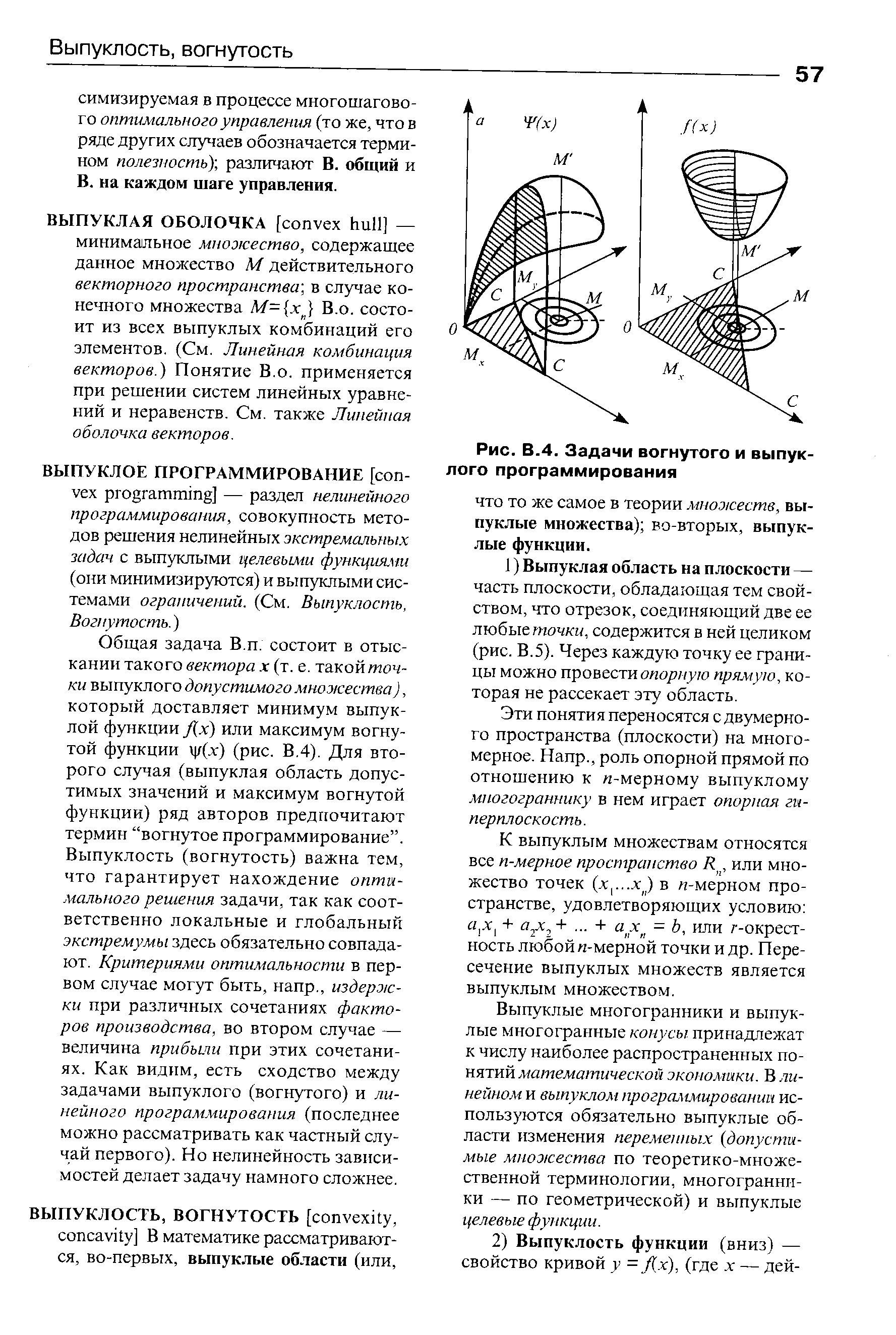 |
Выпуклая область 57 Выпуклая оболочка 57 Выпуклая целевая функция 385 Выпуклое программирование 57 Выпуклость 57 Выпуклость функции 57 Выпуклые множества 57 Выпуклые функции 57 Выпуклый многогранник 198 Выпуск (годовое производство) товаров и [c.462]
Существуют и другие частные разделы нелинейного программирования, для которых разработаны точные методы их решения. Это — выпуклое программирование, частный случай которого — квадратичное программирование. [c.116]
Методы решения таких задач принято называть выпуклым программированием. [c.147]
Несколько отличные от алгоритма Корнай—Липтака декомпозиционные алгоритмы были изложены А. Г. Аганбегяном, К. А. Багриновским, А. Г. Гранбергом [7] Т. Н. (Первозван-ской и А. А. Первозванским [90] и другими авторами. Характерной чертой всех алгоритмов является то, что в основе согласования решения основной модели с решениями подмоделей лежат двойственные оценки. Однако все свойства этих оценок имеют силу только для моделей линейного и выпуклого программирования. Попытки определять и использовать двойственные оценки в задачах с дискретными переменными не привели в настоящее время к значительным успехам. [c.189]
Рийсмаа Т.Д. Об оптимизации структуры иерархической системы методами выпуклого программирования / Методы анализа взаимодействия в экономических системах. Новосибирск Наука, 1980. С. 100 - 106. + + + + + + + + + + п + + [c.18]
ВЫПУКЛОЕ ПРОГРАММИРОВАНИЕ [ onvex programming] — раздел нелинейного программирования, совокупность методов решения нелинейных экстремальных задач с выпуклыми целевыми функциями (они минимизируются) и выпуклыми системами ограничений. (См. Выпуклость, Вогнутость ) [c.57]
КУНА—ТАККЕРА УСЛОВИЯ [Kuhn—Tu ker onditions] — условия существования оптимальной точки (оптимального решения) в задачах выпуклого программирования и, в частности, — линейного программирования. Соответственно этим условиям для того чтобы точка х была оптимальной, необходимо и достаточно, чтобы пара точек (х, X ) образовала седло функции Лагранжа (см. Лагранжиан, Седловая точка). Таким образом, задача сводится к нахождению совместного решения прямой (поиск ж ) и двойственной (поиск X ) задач. Сформулированы американскими математиками X. Куном и А. Таккером. [c.165]
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ [mathemati al programming] (см. также Оптимачьное программирование) — раздел математики, который "... изучает методы решения задач на нахождение экстремума функций (показателя качества решения) при ограничениях в форме уравнений и неравенств"40. Оно объединяет различные математические методы и дисциплины исследования операций линейное программирование, нелинейное программирование, динамическое программирование, выпуклое программирование, геометрическое программирование, целочисленное программирование и др. [c.186]
МНОЖИТЕЛИ ЛАГРАНЖА [Lagrange multipliers] — дополнительные множители, преобразующие целевую функцию экстремальной задачи выпуклого программирования (в частности, линейного программирования) при ее решении одним из классических методов — методом разрешающих множителей (методом Л агранжа). Полученная функция носит название лагранжиан, или функция Лагранжа. Подробнее об этом методе см. в ст. "Лагранжиан". [c.202]
Среди вычислительных алгоритмов Н.п. большое место занимают градиентные методы. Универсального же метода для нелинейных задач нет и, по-видимому, может не быть, поскольку они чрезвычайно разнообразны. Особенно трудно решаются многоэкстремалъпые задачи. Для некоторых типов задач выпуклого программирования (вид нелинейного) разработаны эффективные численные методы оптимизации. [c.222]
Выпуклое программирование оказывается, однако, неэффективным, если при выработке оптимальных моделей используются многоэкстремальные модели. Такие задачи довольно широко распространены на промышленных предприятиях, так как в большинстве отраслей промышленного производства с ростом объема производства удельные затраты сокращаются, изменяясь по параболическому закону. [c.147]
Смотреть страницы где упоминается термин Выпуклое программирование
: [c.15] [c.226] [c.122] [c.75] [c.35] [c.14] [c.144] [c.83] [c.116] [c.101] [c.111] [c.52] [c.58] [c.141] [c.165] [c.59] [c.591]Популярный экономико-математический словарь (1973) -- [ c.117 ]
