Выпуклой оболочкой данного множества называют наименьшее выпуклое множество, содержащее это множество. [c.138]
Выпуклая область 57 Выпуклая оболочка 57 Выпуклая целевая функция 385 Выпуклое программирование 57 Выпуклость 57 Выпуклость функции 57 Выпуклые множества 57 Выпуклые функции 57 Выпуклый многогранник 198 Выпуск (годовое производство) товаров и [c.462]
Если
Оптимальное решение каждой из этих задач либо единственно и равно д , либо имеет переключательный характер и меняется между двумя базовыми значениями. В первом случае выпуклая оболочка функции ДА (неотрицательных значений gi совпадает с графиком этой функции в точке [c.173]
Условие (8.88) означает, что при сд = с выпуклая оболочка функции по(сд) проходит выше ее графика. [c.304]
Из (9.102) следует, что начало координат в пространстве С является внутренней точкой выпуклой оболочки множества, состоящего из точек v (расположено между v). [c.346]
Имеется т+1 уравнений с т+1 неизвестными (А, А ,. . . , А и При найденных значениях А-множителей плоскость, опорная к Соус / (С) и проходящая через точки v, оказывается горизонтальной и отстоящей от начала координат на расстояние R (Q). Изменение наклона гиперплоскости приведет к тому, что значение функции R ( ) в некоторых точках v возрастет и станет больше й (0), а в других уменьшится. Таким образом, никаким изменением А нельзя сделать значение расширенной задачи меньшим значения R (Q). Вместе с тем, R (Q) равно ординате выпуклой оболочки функции достижимости при С = 0, так как добавление слагаемого Aa- f не меняет ординаты [c.346]
В заключение отметим, что опорная гиперплоскость может пройти не через m + 1, а через меньшее число точек выпуклой оболочки. В этом случае некоторые из jv в (9.102) обращаются в нуль. Число одинаковых максимумов функции R ( ) меньше m + 1, однако для этих максимумов условия (9.103) выполнены и все проведенные выше рассуждения остаются в силе. [c.347]
Вернемся к задаче (9.158) и попытаемся привести ее также к задаче построения выпуклой оболочки функции. Для этого воспользуемся тем обстоятельством, что задачу (9.158) можно решать в два этапа. На первом этапе найдем максимум функции /о (а ) при условиях f(x] — С где С принимает все те значения, при которых поверхность уровня f(x] — С пересекается с множеством Vx. Задача [c.367]
Эта задача аналогична задаче (9.160). Ее значение, а следовательно, и значение задачи (9.158) равно ординате выпуклой оболочки функции достижимости /о (С) для С = 0 [c.368]
| Рис. 9.17. Функция достижимости и ее выпуклая оболочка для случая, когда множество допустимых решений исходной задачи НП пусто | 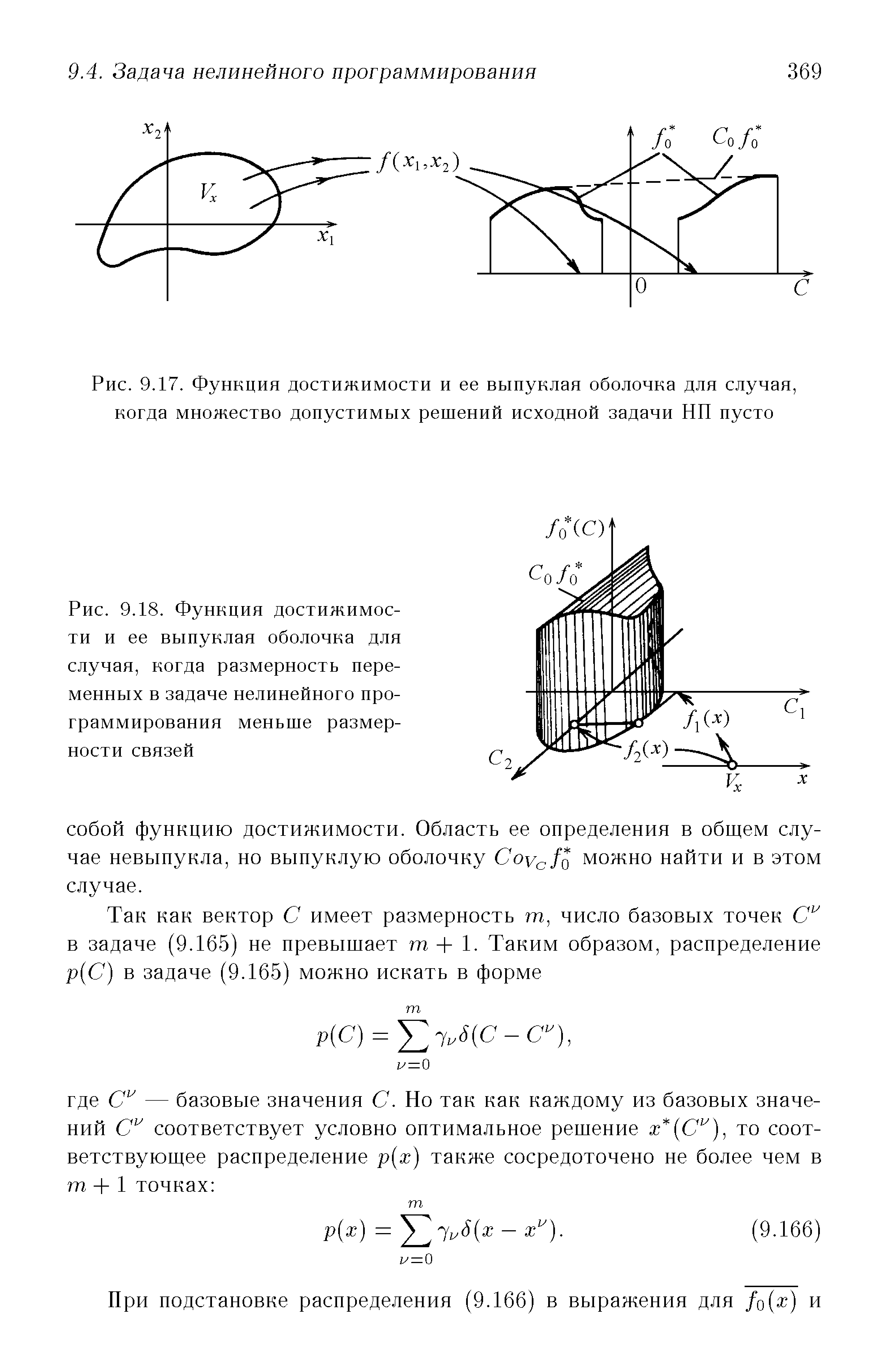 |
| Рис. 9.18. Функция достижимости и ее выпуклая оболочка для случая, когда размерность переменных в задаче нелинейного программирования меньше размерности связей | 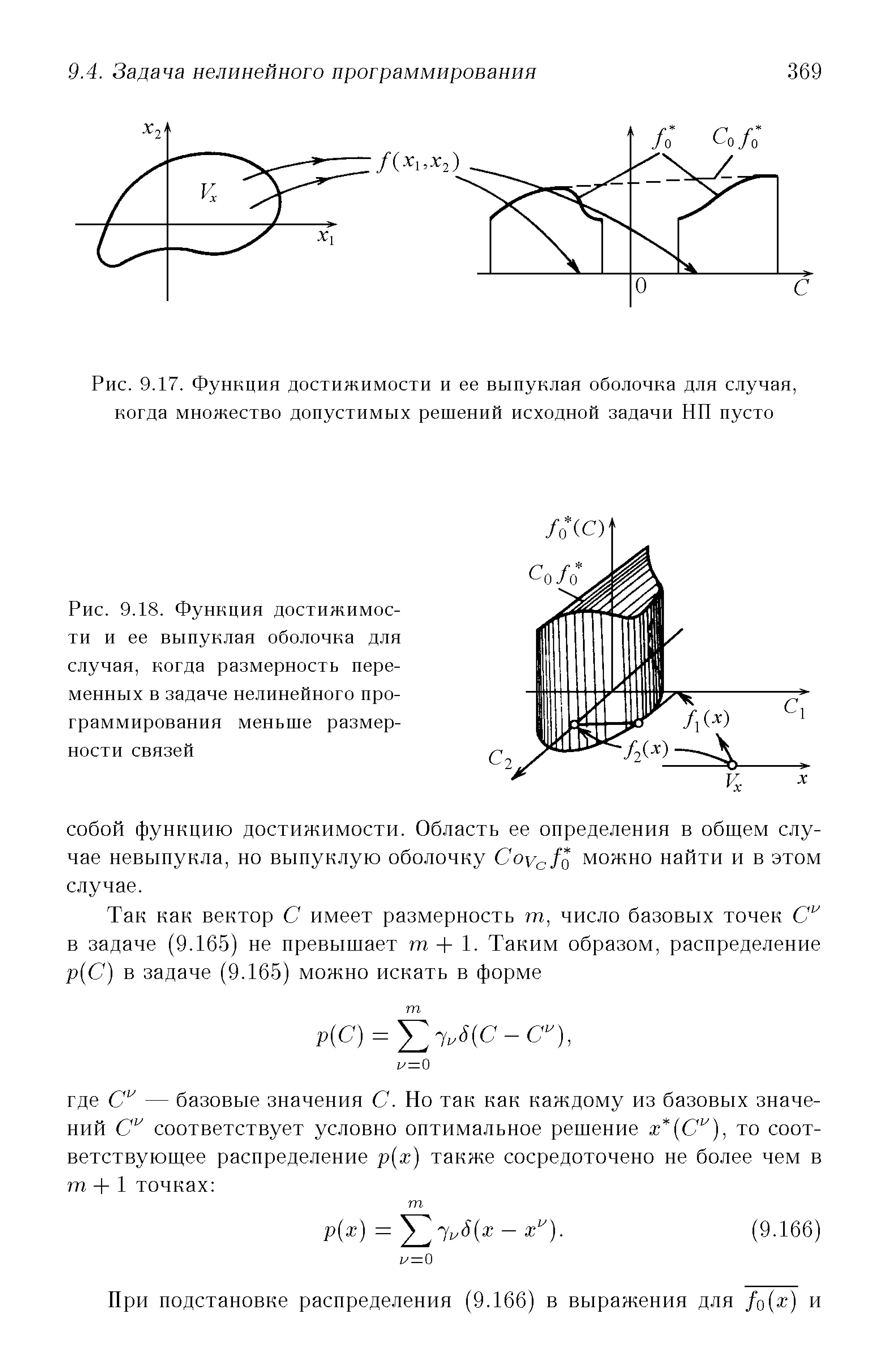 |
Так как множество значений а , удовлетворяющих этим условиям, представляет собой выпуклую оболочку множества L>, то задача (9.173) эквивалентна задаче НП, но на множестве значений х, принадлежащих выпуклой оболочке множества L>, [c.373]
Условие (6.15) показывает ограничения на объемы перекачки, в том числе сверху — на пропускную способность соответствующего участка нефтепровода. Формула (6.16) выражает для каждой вершины сети баланс между суммарным поступлением нефти извне системы и от других вершин сети- и суммарным потреблением, включая собственно потребление в самой вершине и перекачку нефти к другим вершинам сети и вне системы. Целевая функция (6.17)—критерий минимизации суммарных энергозатрат перекачки по всей системе. Функции frs(xrs) — кусочно-линейные и выпуклые (вниз). Каждая из них соответствует минимально возможным энергозатратам на перекачку различных объемов нефти по отдельным участкам системы. Строятся функции frs(XrS) по методу огибающей, т. е. находится нижняя граница выпуклой оболочки точек, характеризующих фиксированные режимы работы соответствующих насосных агрегатов и их комбинаций [26]. [c.156]
Вычисление апостериорных решающих правил стохастической задачи (3.7) — (3.9) в общем случае связано со значительными трудностями. Однако в случае, когда пространство Q элементарных событий состоит из конечного числа (г) элементов, вероятности которых заданы, решение задачи упрощается. Построение выпуклой оболочки множества [c.141]
Этим исчерпывается информация, которую можно извлечь из условия (g, ЪР) 0 для ЪР К так как К, есть выпуклая оболочка векторов е, е(1 е(2),. .., с -. [c.72]
Перейдем к вопросам сходимости в вычислительной схеме Н. Н. Моисеева. Основное осложнение связано с тем, что теперь в разностной задаче (7) точки х могут принимать лишь дискретные значения а ., принадлежащие сетке 5. Поэтому в принципе может оказаться, что ни для какой пары точек из соседних сеток я., ж +1 не удастся построить соединяющей их траектории (1) на малом интервале [tt, t +1]. В этом случае разностная задача просто не имеет решения. Чтобы избежать этой опасности, следует наложить определенные ограничения на /г-шаг сетки по фазовым координатам. Кроме того, нужно гарантировать разрешимость элементарной операции. Эти вопросы исследовались в работах [56], [37]. Разрешимость разностной задачи и сходимости численного решения к решению задачи (1)—(5) была доказана в предположении некоторых свойств непрерывности функции Беллмана решаемой задачи. Однако для практики вычислений более существенным является другое условие шаги сетки hr по r-й компоненте фазового пространства должны быть связаны с шагом сетки по времени т соотношением ftr=T1+P>-, где рг 1 — некоторые числа, зависящие от строения области достижимости за малое время т для системы (1). Напомним, что областью достижимости D (Z, t) называется совокупность правых концов траекторий системы x=f (х, и), х (0)=z при произвольных измеримых и (t), и ( ) U, О t т. В работе автора [93] те же вопросы были решены только с одним предположением h—0 (t2). При этом под элементарной операцией следует понимать решение следующей простой геометрической задачи, являющейся аппроксимацией дифференциальной на малом интервале времени. Для расширенной системы (1) (пополненной уравнением x°=f(x, u), х° (0)=0) строится в каждой точке х область x- -tf (х, U) (если / (х, U) не выпукла, следует заменить ее выпуклой оболочкой). Далее эта область расширяется присоединением всех сфер радиуса ft2 с центрами в ж+т/ (x1U), Полученную область в пространстве х°, х1,.. ., хп обозначим DT (х), а ее проекцию на гиперплоскость х1, а 2,. ... . ., х" — jD (х). Если шаги сеток А=ста, то при определенном соотношении между с и С можно утверждать, что для любой точки xlj 5" найдется хотя бы одна точка xj.+i 5 41 такая, что [c.125]
Напомним, что / (х, U) есть выпуклая оболочка совокупности точек / (х, и) при всех и U. [c.129]
Конструкция 8Е/Я+1/,- Опуская для простоты индекс гс+ /а, опишем применявшийся в наших расчетах способ описания Ъи. Мы предполагаем, что множество допустимых по условию и ( )+8м (t) Si7 (t) вариаций образует выпуклый конус Kt в r-мерном пространстве (г — размерность и). Как известно, выпуклые конусы допускают два способа описания либо как пересечение некоторого набора полупространства, либо как выпуклая оболочка набора векторов. Именно этот второй способ и оказывается наиболее удобным. [c.168]
ВЫПУКЛАЯ ОБОЛОЧКА [ onvex hull] — минимальное множество, содержащее данное множество М действительного векторного пространства в случае конечного множества М- х В.о. состо- [c.57]
Доказательство теоремы 9.1. При фиксированном х Е Ух значения вектор-функции / в задаче (9.34), (9.35) принадлежат множеству Q> которое представляет собой отображение множества Vu в m-мерное пространство /. Значения же вектора / принадлежат выпуклой оболочке Q. Согласно теореме Каратеодори каждый элемент [c.321]
Действительно, совершенно аналогично тому, как это было сделано выше при доказательстве теоремы 9.1., можно доказать справедливость первого из утверждений лемммы 9.5 здесь при любом фиксированном значении , х, а, г значения вектора / = (/0, /х,. .., /т) принадлежат выпуклой оболочке множества Q> получающегося при отображении Vu в (т + 1)-но мерное пространство /. Так как искомое решение максимизирует /о по [7, то оно принадлежит верхней границе Q и может быть получено как линейная комбинация (т + 1)-го элемента Q. [c.325]
Выпуклой оболочкой функции называют выпуклую оболочку множества, лежащего под графиком функции (подграфика). В свою очередь выпуклой оболочкой множества М в пространстве Rn называют множество, включающее все элементы М и элементы Rn, которые могут быть получены посредством операции усреднения элементов множества М. [c.345]
Построим выпуклую оболочку ova/Q (С) функции достижимости [c.345]
Таким образом, если в точке С = 0 функция достижимости и ее выпуклая оболочка совпадают, то расширение Лаграижа эквивалентно (достаточное условие эквивалентности). [c.346]
Здесь черта соответствет усреднению на множестве Vx. Значение задачи (9.160), как это следует из определения выпуклой оболочки функции, равно ординате выпуклой оболочки функции /о(а ) на множестве Vx в точке х — 0. Так как построение любой ординаты выпуклой оболочки функции п переменных, согласно теореме Каратеодори, требует усреднения не более чем (п - - 1)-й ординаты функции /о(а ), задачу (9.160) можно переписать в форме [c.367]
Заметим, что множество допустимых решений задачи нелинейного программирования (9.81) может быть пусто, т.е. внутри Vx, например, нет элементов, для которых fi(x) равнялись бы нулю. При этом функция /о (С) не определена в точке С = 0. Однако для построения ova/Q множество V дополняют до его выпуклой оболочки, и на дополнительных участках / (С) считают достаточно малой. При этом oy /Q на этих участках определена. На рис. 9.17 приведен пример функции достижимости и ее выпуклой оболочки. Решение исходной задачи отсутствует, так как для любого х Е Vx функция / не равна нулю. Усредненная задача имеет решение, которому соответствует значение целевой функции, равное " v /g(0). [c.368]
В том случае, когда любое из сечений /о (0, i) или /о (0, j) невыпукло в нуле, т.е. когда выпуклая оболочка этой функции на V имеет для С = 0 ординату, большую ординаты самой функции, расширение Лагранжа задачи НП не эквивалентно. Выпуклость в нуле даже всех сечений функции достижимости (рис. 9.20) координатными плоскостями, естественно, не гарантирует эквивалентности расширения Лагранжа, так как [c.372]
Теорема Каратеодори. Пусть A<=Rm — компакт. Тогда каждая точка со А (выпуклой оболочки множества А) есть выпуклая комбинация не более чем т+1 точки множества А, т. е. [c.22]
Отображение (3.10) переводит множество X zRn в Ус/ +1. В общем случае У — невыпуклое и незамкнутое множество. Обозначим через соУ выпуклую оболочку множества У. Задача (3.1) — (3.3) может быть переписана в виде [c.138]
Согласно теореме Каратеодори [87] для построения выпуклой оболочки множества У из т+ 1-мерного пространства требуется в общем случае не более т + 2 точек уеУ. Это значит, что со У может быть предстазле-138 [c.138]
Здесь/(ж, U) есть совокупность точек /(ж, м) ер, a onvf(x, U) — выпуклая оболочка f(x, U). [c.86]
Область / (х, U) изображена на рисунке 8 для двух случаев 1) и 1и2)м—1 или —1. В том и другом случае множество / (х, U) невыпукло и штриховкой показана его выпуклая оболочка onv / (х, U). Изображенное на рис. 7 ) решение на интервале t 2 удовлетворяет уравнению [c.86]
Р. В. Гамкрелидзе предложил следующий прием сведения задачи с невыпуклым множеством / (х, U) к задаче с выпуклым. В сущности, это есть способ стандартного аналитического описания дифференциального включения z(< onv / (х, U). В теории выпуклых множеств известен следующий факт любую точку выпуклой оболочки / (х, U) можно получить в виде [c.88]
Смотреть страницы где упоминается термин Выпуклая оболочка
: [c.310] [c.62] [c.237] [c.144] [c.322] [c.346] [c.346] [c.346] [c.347] [c.369] [c.22] [c.141] [c.148] [c.88] [c.266]Приближенное решение задач оптимального управления (1978) -- [ c.86 , c.125 ]
Справочник по математике для экономистов (1987) -- [ c.84 ]
