Доказательство. На основании необходимых и достаточных условий разрешимости задачи об управлении, сформулированной в форме проблемы моментов, область достижимости имеет вид [c.81]
С применением методов оптимизации и оптимального управления исследованы предельные возможности тепловых, химических, массообменных процессов при заданной средней интенсивности целевого потока. Аналогия между термодинамическими и микроэкономическими системами позволяет перенести методологию термодинамики при конечном времени на микроэкономику, введя количественные показатели необратимости процессов и, в частности, экономический аналог диссипации. Рассмотрен класс процессов минимальной диссипации, определяющих через уравнения термодинамических и микроэкономических балансов область достижимых режимов. [c.2]
Связь, аналогичную равенству (3.10), нетрудно получить и для любой заданной зависимости с(ТЬ) теплоемкости от температуры источника. Области достижимости для конкретных законов теплопередачи. [c.114]
| Рис. 3.2. Области достижимости для произвольного процесса теплообмена с линейным законом теплопередачи (а) и законом | 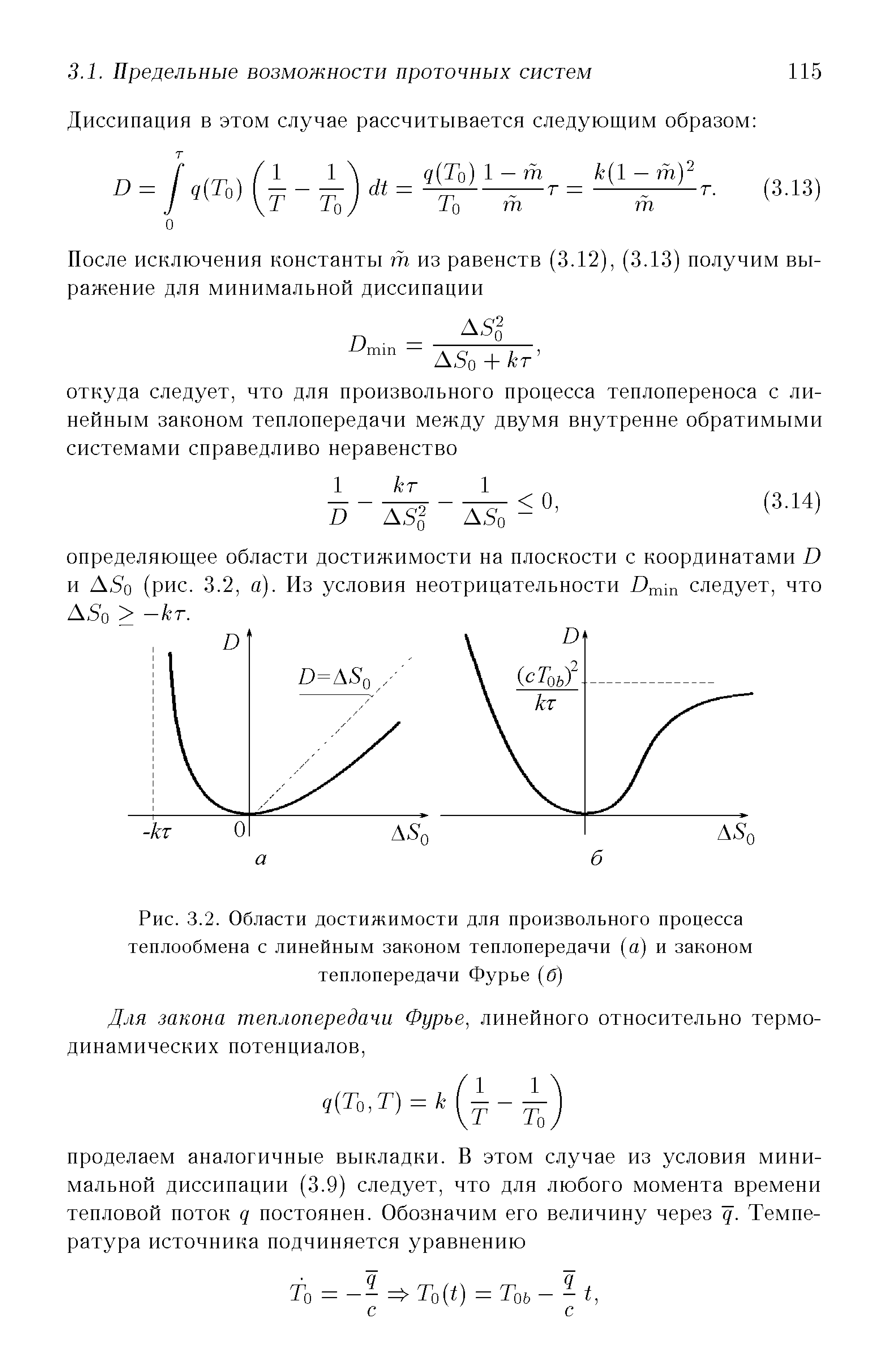 |
Такое управление называют допустимым в области достижимости ему соответствует точка F [и( )], лежащая на оси F0 пусть построен конус смещений Кр (рис. 4). Если управление и( ) — оптимально, конус Кр не должен содержать направления е — — 1, 0, 0,. . . 0 . В самом деле, если е ( KF, то существует вариация управления 8и( )( Ки такая, что порожденное ею смещение 8/ [8в( )] = 8/ 0, О, 0,, . ., 0 и Wn<0, т. е, значение F9[u( ) + to(- )]
Перейдем к вопросам сходимости в вычислительной схеме Н. Н. Моисеева. Основное осложнение связано с тем, что теперь в разностной задаче (7) точки х могут принимать лишь дискретные значения а ., принадлежащие сетке 5. Поэтому в принципе может оказаться, что ни для какой пары точек из соседних сеток я., ж +1 не удастся построить соединяющей их траектории (1) на малом интервале [tt, t +1]. В этом случае разностная задача просто не имеет решения. Чтобы избежать этой опасности, следует наложить определенные ограничения на /г-шаг сетки по фазовым координатам. Кроме того, нужно гарантировать разрешимость элементарной операции. Эти вопросы исследовались в работах [56], [37]. Разрешимость разностной задачи и сходимости численного решения к решению задачи (1)—(5) была доказана в предположении некоторых свойств непрерывности функции Беллмана решаемой задачи. Однако для практики вычислений более существенным является другое условие шаги сетки hr по r-й компоненте фазового пространства должны быть связаны с шагом сетки по времени т соотношением ftr=T1+P>-, где рг 1 — некоторые числа, зависящие от строения области достижимости за малое время т для системы (1). Напомним, что областью достижимости D (Z, t) называется совокупность правых концов траекторий системы x=f (х, и), х (0)=z при произвольных измеримых и (t), и ( ) U, О t т. В работе автора [93] те же вопросы были решены только с одним предположением h—0 (t2). При этом под элементарной операцией следует понимать решение следующей простой геометрической задачи, являющейся аппроксимацией дифференциальной на малом интервале времени. Для расширенной системы (1) (пополненной уравнением x°=f(x, u), х° (0)=0) строится в каждой точке х область x- -tf (х, U) (если / (х, U) не выпукла, следует заменить ее выпуклой оболочкой). Далее эта область расширяется присоединением всех сфер радиуса ft2 с центрами в ж+т/ (x1U), Полученную область в пространстве х°, х1,.. ., хп обозначим DT (х), а ее проекцию на гиперплоскость х1, а 2,. ... . ., х" — jD (х). Если шаги сеток А=ста, то при определенном соотношении между с и С можно утверждать, что для любой точки xlj 5" найдется хотя бы одна точка xj.+i 5 41 такая, что [c.125]
Стоит разъяснить возможное в связи с этим недоразумение. Хорошо известно, что область достижимости за время т для управляемой системы обычно имеет существенно разные размеры по разным координатам. Так, для системы [c.126]
Определение. Множество точек F [и ( )] = F0 [и ( )],. , .., Fm [u(-) в (т+1)-мерном евклидовом пространстве, порожденное всеми возможными измеримыми функциями и (t), определенными на [О, Т] и удовлетворяющими геометрическому ограничению и (t) U, называется областью достижимости D для задачи [c.188]
Предположение о строгой выпуклости области достижимости D существенно ограничивает область применимости метода, причем нарушение строгой выпуклости не только лишает силы доказательство сходимости, но и ликвидирует саму сходимость. В реальных нелинейных задачах проверка строгой выпуклости D фактически невозможна, предполагать же ее имеющей место нет никаких оснований. Так, в первой же задаче, в которой была численно найдена граница D (см. 29, рис. 26), область D оказалась вогнутой. [c.190]
В этом случае, при выпуклой области U, область достижимости D оказывается строго выпуклой. (Это не очень точно, строгая выпуклость доказывается при некоторых предположениях, однако они выделяют общий случай, и нарушение строгой выпуклости следует считать вырождением.) [c.191]
Важную роль в дальнейшем играют следующие объекты D (t) — область достижимости за время t — это совокупность всех точек х, в которые траектория системы (14) может попасть под воздействием какого-то управления за время t t G (t)—dtD (t) — граница D (t) ). [c.192]
Достижимы ли такие условия в совместных проектах в области электроники (например, сверхбольших интегральных схем) Вряд ли, потому что техника в этой области идет вперёд настолько быстро, что в течение одного-двух лет ситуация может коренным образом измениться. Каждые два года технические характеристики сверхбольших интегральных схем улучшаются в четыре раза. При таком темпе решения должны приниматься обдуманные, взвешенные, но быстрые. Это маловероятно в совместных проектах, когда менеджеры всех фирм — участниц проекта должны принимать решения сообща. [c.230]
Методы принятия решения при нескольких критериях превратились в самостоятельную область исследования совсем недавно, в семидесятых годах нашего века. Мы посвятим этим методам отдельный параграф гл. 6. Заранее отметим, что в качестве математического средства решения многокритериальных проблем используются методы оптимизации (в линейном случае — методы линейного программирования), а также некоторые другие методы (например, для построения множества достижимых значений показателей— методы теории линейных неравенств). [c.61]
После назначения на Вашем предприятии ответственных за подразделения целесообразно привлечь их к обсуждению плана, учесть их аргументы и мнения и тем самым убедиться, что эти лица ознакомлены с областью своей ответственности и связанными с этим целями. Планирование — это всегда компромисс между достижимым и желаемым. Планы, которые нельзя выполнить, или условия реализации планов, при которых они оказались невыполненными, недостаточно мотивированы. Здесь желаемое оказалось выше реального. И, наоборот, планы, только продолжающие прошлое без новых идей и запланированного улучшения показателей, лишены силы. [c.80]
Неоспорим также факт, что учет часто нуждается в информации, относящейся к области будущего. Например, только доподлинные сведения о том, за какую цену и когда именно будет продан товар в будущем, позволят определить, за сколько его стоит покупать для перепродажи в настоящий момент. Владей учет подобной информацией, ценность этой дисциплины для хозяйственной деятельности несказанно повысилась бы. Однако информация становится достижимой не раньше момента наступления события, с которым она связана. По этой причине учет вынужден прогнозировать будущее, предполагая, к примеру, что это оборудование будет окончательно изношено через десять лет после приобретения, а этот долг, увы, уже никогда не будет получен с должника. [c.101]
Квадрант В. Для этой области графика характерно превышение достижимой цены над мировой, причем издержки производства не отличаются значительной величиной. Их размер меньше не только достижимой, но и действующей в настоящее время мировой цены. [c.27]
Вывод это область умеренной рентабельности от экспорта данного изделия, так как достижимая цена уступает ценам зарубежного изделия-аналога. [c.28]
Вывод это область нерентабельного (убыточного) экспорта из-за низкой (ниже расходов на изготовление) достижимой цены на зарубежном рынке. [c.28]
Всякая механическая работа сводится к перемещению массы в пространстве. Но мы уже отмечали, что такое перемещение достижимо и помимо человеческих усилий, в результате стихийных сил природы, а также работы машин и животных. Стало быть, далеко не всякая работа сопряжена с трудом и, наоборот, не всякий труд дает в результате перемещение тяжестей, т. е. механическую работу. Например, если моей спиной воспользуются как площадкой для поддержки грузов, то, несмотря на большую трату физических усилий, а стало быть, и энергии, я не произведу в процессе этого труда никакой механической работы. Точно так же, решая в уме математическую задачу, я, несомненно, затрачиваю немало умственных усилий за счет наличной в организме энергии, молекулы моего мозга при этом, вероятно, очень активно вибрируют, но все же это не дает никакого перемещения масс в пространстве, никакой механической работы. Таким образом, область механической работы, с одной стороны, гораздо шире, а с другой — много уже области труда. [c.16]
Однако, при увеличении размеров элементарного блока, появляется область высоких степеней сжатия, достижимых лишь с использованием квантования. Скажем, при d - 64 х 64 - 4096, когда djb = 64, в соответствии с графиком (см. Рисунок 11), квантование следует применять [c.83]
В этой главе предполагалось, что инвестор может получить взаймы средства по той же самой ставке, по которой он может их инвестировать в безрисковый актив. В результате множество достижимости приобрело вид области, ограниченной двумя лучами, исходящими из точки, соответствующей безрисковой ставке. Верхняя линия представляла эффективное множество и пересекалась только по одному портфелю с эффективным множеством модели Марковица. Этот портфель соответствовал точке касания данного луча с эффективным множеством модели Марковица. Теперь рассмотрим, что произойдет, если предположить, что инвестор может получить заем, но по ставке, превышающей доходность от инвестирования в безрисковый актив. Ставка по безрисковому активу обозначается rfi, где L означает предоставление займа, потому что, как уже говорилось, инвестирование по безрисковой ставке эквивалентно предоставлению займа правительству. Ставка, по которой инвестор может получить заем, обозначается rfg и удовлетворяет условию rfi > rfL. [c.250]
Для ответа на данный вопрос полезно рассмотреть следующие альтернативные допущения (I) инвесторы могут вкладывать деньги без риска, т.е. приобретать активы, обеспечивающие безрисковую доходность со ставкой г (2) инвесторы могут занимать деньги без ограничения объема под более высокий процент г/в. Эти безрисковые ставки указаны на вертикальной оси рис. Ю.З. Область на графике, имеющая форму зонтика, включает комбинации риска и доходности, достижимые путем инвестиций исключительно в рискованные активы 5. [c.277]
Кроме того, следует отметить, что данный метод можно использовать в комбинации с некоторыми другими известными приемами решения многокритериальных задач. Так например, в конце шестой главы обсуждается возможность комбинирования метода последовательного сужения области компромиссов вместе с методом целевого программирования и методом достижимых целей. [c.14]
В этой главе после краткого предварительного рассмотрения вопросов, связанных с процессом принятия решения человеком, излагается метод последовательного сужения множества Парето (области компромиссов) на основе количественной информации об относительной важности критериев. Теоретические предпосылки применения этого метода были разработаны в предыдущих главах, а здесь дается его описание без математических подробностей и приводятся некоторые рекомендации по применению. Кроме того, изучается возможность комбинирования этого метода с методом целевого программирования и методом достижимых целей. [c.145]
Аудит целей и стратегий маркетинга. Такого рода анализ призван показать состоятельность и достижимость главной цели предприятия или фирмы (миссии) и основных целей в области маркетин- [c.464]
Переход от чистых стратегий к смешанным расширяет область определения задачи. Достижимый максимум целевой функции может при этом только увеличиться, а достижимый минимум — только уменьшиться. Вычисление оптимальной смешанной стратегии иногда называют определением решающего распределения стохастической задачи. [c.12]
Рассмотрим рис. 1. Здесь по оси абсцисс показана полезность одного из потребителей, скажем, Андрея. По оси ординат — полезность другого, назовем его Борисом. Область OFF — это область потребительских возможностей. Она включает в себя и свою границу с правой стороны, так называемую кривую возможных полезностей. Андрей и Борис могут потребить любой набор благ в пределах их наличного количества, при этом они могут оказаться как в эффективном состоянии ( выжать всю возможную полезность и оказаться в какой-либо точке на кривой возможных полезностей), так и в неэффективном, т. е. недобрать потенциально достижимую полезность, а значит, оказаться левее кривой возможных полезностей, предположим, в точке G. [c.249]
Если новая техника, новые технологические процессы будут внедряться одновременно и равномерно во всех отраслях, то граница производственных возможностей AD на рис.2 сдвинется в положение пунктирной линии A D, возможности выпуска и средств производства, и предметов потребления при тех же ресурсах увеличатся примерно в равной степени. И точка Е, лежащая вне прежних границ области производственных возможностей ОАО, окажется теперь вполне достижимой. [c.13]
Этим и заканчивается стандартный шаг процесса максимизации t (
В качестве исходной композиции была выбрана защита, состоящая из чередующихся слоев воды и железа. Построенный в этой ситуации конус KF изображен на рис. 36, причем, так как точки и занимают угловые позиции в области U, здесь имеются только односторонние векторы. Пересечения соответствующих лучей с плоскостью F0 = 1 обозначены + , пересечения с плоскостью 8/ 0 = — 1 обозначены . Нужно еще учесть, что для разных групп векторов h пришлось использовать разные масштабы если бы масштаб был единым, разброс точек был бы еще большим. Анализ этой ситуации с очевидностью приводит к выводу, что конус KF заполняет все трехмерное пространство. На рис. 37 изображены концентрации компонент защиты, найденные в результате решения вариационной задачи. С точки зрения уменьшения веса железо выгоднее передвинуть во внутренние области защиты. Однако, так как при этом происходит увеличение генерации захватного у-излучения, в эти области приходится добавлять большие по сравнению с наружными областями количества бора. Вес одного погонного сантиметра защиты в исходной композиции равен 290 кг, для оптимального варианта 190 кг. Структура конуса достижимости KF в оптимальной ситуации выясняется с помощью рис. 38. На нем изображены следы лучей, порожденных свободными векторами h (изображены ). Эти следы расположены вблизи двух [c.273]
Низкая производительность может объясняться избыточными объемами вводимых в производство ресурсов или неправильно выбранной структурой этих ресурсов. На графике низкая производительность отображается высокой кривой предельных издержек. Этот случай проиллюстрирован на рис. 2.6 двумя кривыми предельных издержек. Область между верхней кривой и нижней кривой, находящейся, как мы предполагаем, на низшем из возможных уровней, измеряет степень неэффективности производства, представленного кривой Л/С/,. В общем случае производственная эффективность означает степень приближения фактических издержек производства к самым низким из достижимых. Понятия А -неэффективности, означающей потери в производстве, и эффективности выбора производственной технологии являются элементами общей концепции производственной эффективности. [c.40]
Неравенство (2.108) задает области достижимых значений параметров состояния в плоскости с координатами (Т>, ASo) при каждом г (линии изохрон), показанные на рис. 2.3. Оптимальные траектории — прямые линии, выходящие из начала координат, так как dD 1 [c.78]
Можно ли доказать подобные теоремы для метода трубки при том бесхитростном способе построения сеток, который показан на рис. 14, или сетки следует строить с учетом структуры области достижимости для траектории x=f за малое время t — неизвестно. Однако и контрпримера, аналогичного контрпримеру для метода локальных вариаций, насколько известно автору, не построено. [c.134]
На рис. 20 качественно изображены введенные выше объекты область достижимости D (t ), ее граница G (t ), траектория х (t), определяемая решением П-системы с началъным вектором ф0, [c.194]
Рисунок 9.7 изображает, как изменяется допустимое множество, если введена возможность как предоставления, так и получения займа по одной и той же безрисковой процентной ставке. Рассматриваются не только акции РАС и Able, но и все остальные рискованные активы и портфели. Множество достижимости представлено областью, расположенной между двумя лучами, выходящими из точки, соответствующей безрисковой ставке, и проходящими через точки, соответствующие акциям Baker и портфелю, обозначенному через Т. Эти два луча уходят в бесконечность при условии, что нет ограничений на величину получаемого займа. [c.244]
