Рассмотрим рис. 1. Здесь по оси абсцисс показана полезность одного из потребителей, скажем, Андрея. По оси ординат — полезность другого, назовем его Борисом. Область OFF — это область потребительских возможностей. Она включает в себя и свою границу с правой стороны, так называемую кривую возможных полезностей. Андрей и Борис могут потребить любой набор благ в пределах их наличного количества, при этом они могут оказаться как в эффективном состоянии ( выжать всю возможную полезность и оказаться в какой-либо точке на кривой возможных полезностей), так и в неэффективном, т. е. недобрать потенциально достижимую полезность, а значит, оказаться левее кривой возможных полезностей, предположим, в точке G. [c.249]
Заметим, что контрактная кривая является аналогом кривой возможных полезностей, только в первом случае на осях откладываются количества благ, а во втором — уровни полезности индивидов, получаемые от наборов благ. Если предположить, что уровень полезности измерим количественно, мы сможем построить рис. 1 по данным об уровнях полезности на контрактной кривой на рис. 3. [c.256]
Без введения количественной меры полезностей наборов благ X и Y о форме этой кривой нельзя сказать ничего определенного, и поэтому кривую возможных полезностей, как правило, изображают не имеющей постоянного знака выпуклости. Единственное, что можно сказать определенно, так это то, что она должна иметь отрицательный наклон. Ведь увеличение уровня no- [c.256]
| Рис. 5. Кривая возможных полезностей при наличии внешних эффектов в потреблении. | 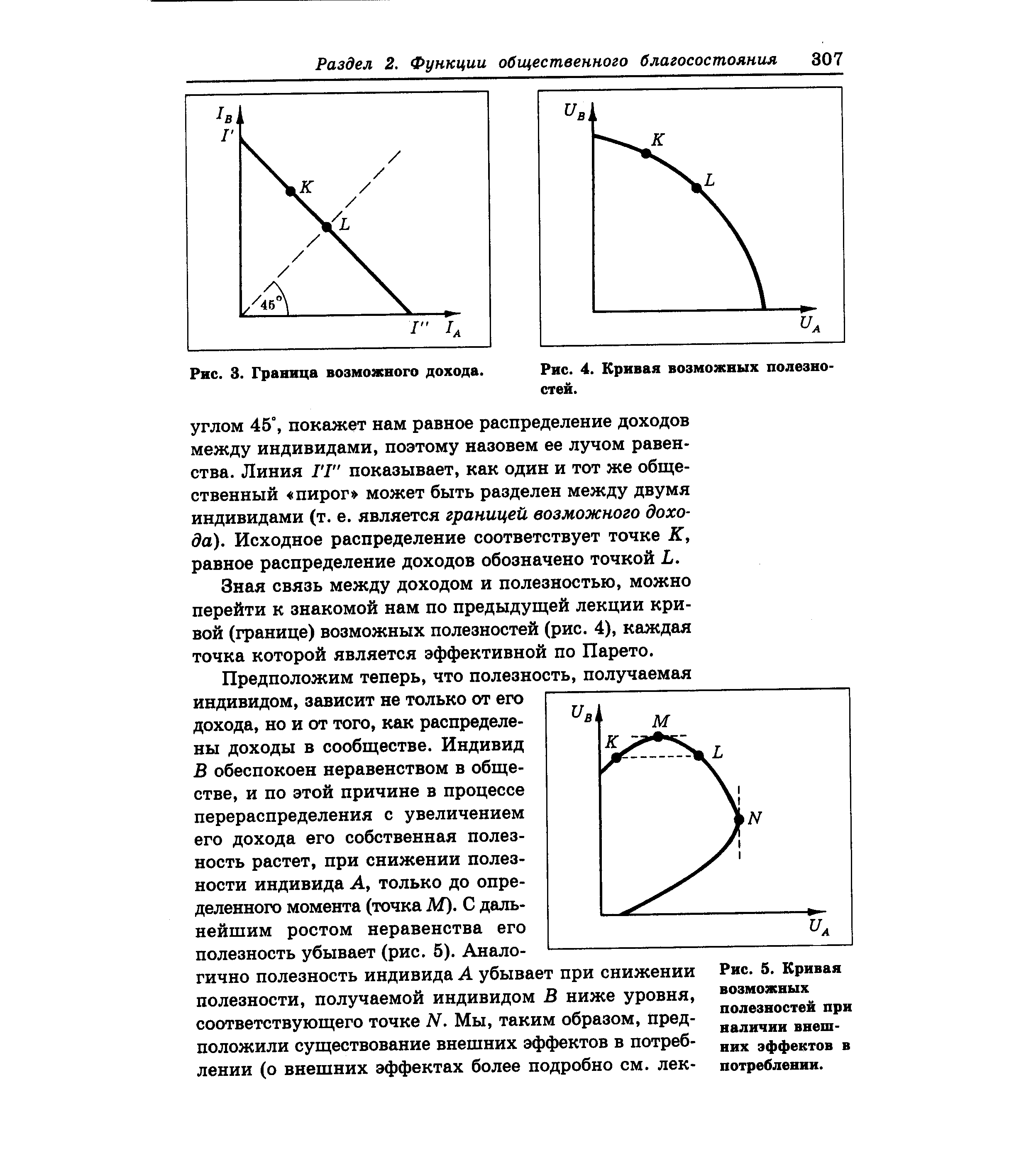 |
Граница возможных полезностей на рис. 15.7 представлена всеми точками, соответствующими эффективным распределениям. Одной крайней точкой является Oj, на которой у Джеймса не остается товаров и поэтому у него нулевая полезность на противоположной крайней точке О к товаров нет у Карины. Все остальные точки на границе, такие, как Е, F и G, соответствуют точкам на кривой контрактов, и поэтому здесь невозможно улучшить положение одного, не ухудшая положения другого. Точка Н представляет неэффективное распределение, поскольку любые сделки в заштрихованной зоне улучшают состояние одной или обеих сторон. В точке L обоим лицам было бы лучше, однако она недостижима, потому что общего запа- [c.433]
Граница возможных полезностей определяет все эффективные распределения (лежащие на кривой контрактов) в терминах уровней полезности, достигаемых каждым лицом. Хотя оба индивида предпочитают неэффективным распределениям некоторые другие, не всякому неэффективному распределению должно быть отдано предпочтение. [c.454]
Очевидно, что семейство прямых ,<2), q , q <73<3) . .. и т.д. имеет аналогичный смысл для групп потребителей с доходом х,, х3,. .. и т.д. Среди разнообразных кривых безразличия потребитель стремится выбрать ту, которая наиболее отдалена от начала координат. Последняя кривая представляет структуру потребительских расходов, соответствующую наивысшей возможной полезности — t/. (рис. 11.4). [c.238]
В течение длительного времени в марксистской экономической теории кривые безразличия не рассматривались как возможный полезный инструмент. Более того, они являлись в основ- [c.248]
Зная связь между доходом и полезностью, можно перейти к знакомой нам по предыдущей лекции кривой (границе) возможных полезностей (рис. 4), каждая точка которой является эффективной по Парето. [c.307]
Кривые доходности строятся путем нанесения на график в рамках единой системы координат величин доходности для группы выпусков облигаций, аналогичных во всех отношениях, кроме срока погашения. Например, казначейские облигации однородны по качеству и характеристикам выпуска, а кривые доходности таких облигаций широко публикуются в финансовой прессе. Некая конкретная кривая доходности существует только в течение короткого отрезка времени по мере изменения условий рынка меняются ее форма и расположение. Информация об вменениях формы и расположения кривых доходности полезна при формулировании представлений о поведении процентных ставок в будущем и о том, как это поведение отразится на динамике курсов и сравнимых доходах. Способы построения кривых доходности и возможности их использования более подробно излагаются во вставке "Проницательному инвестору". [c.459]
| Рис. 15.5. Кривая достижимой (возможной) полезности | 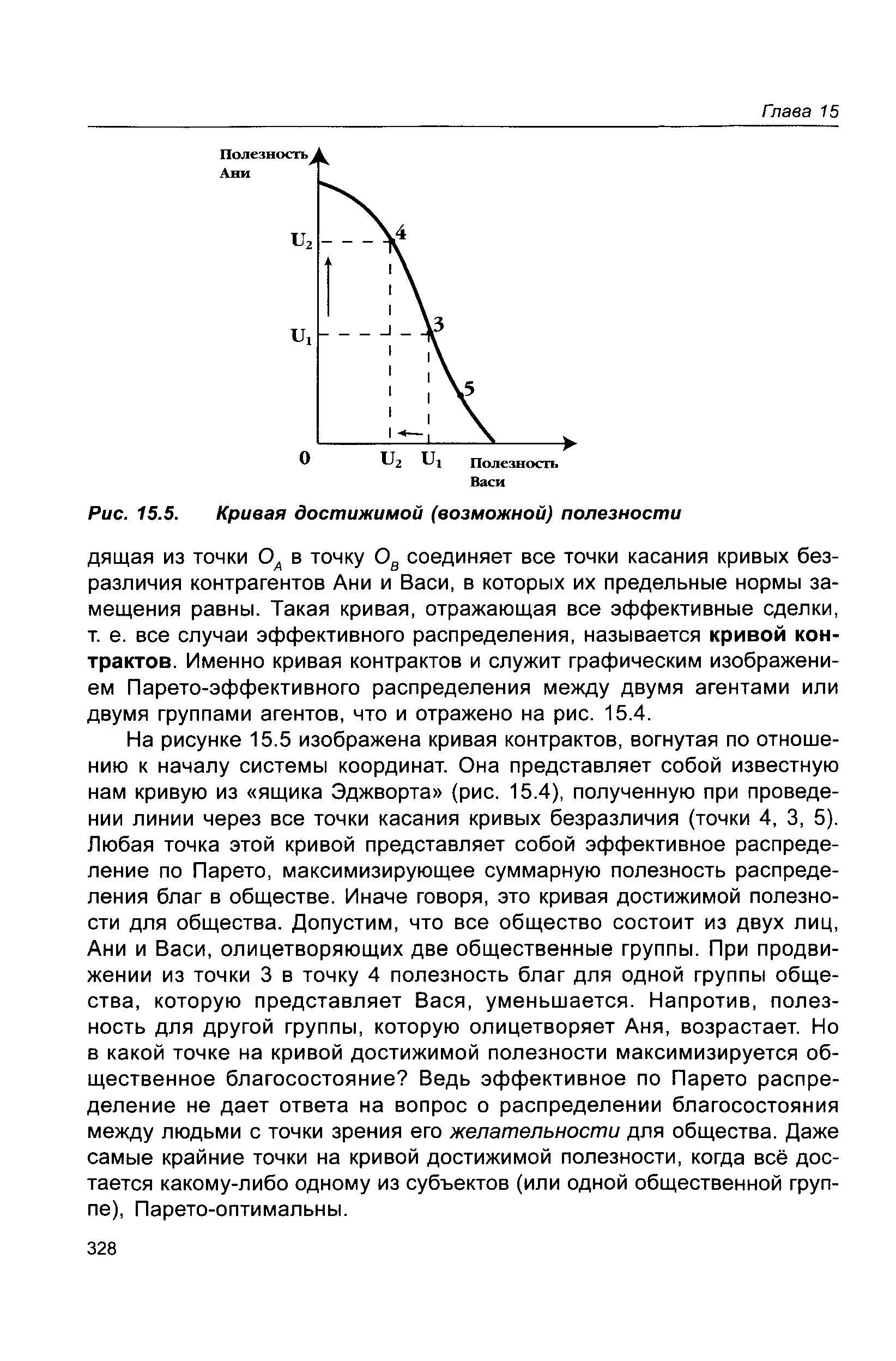 |
Итак, поскольку эффективность по Парето не дает нам никакого критерия для ранжирования точек, лежащих на известной нам из гл. 15 кривой потребительских возможностей (кривой достижимой полезности), мы не можем сказать, что распределение в точке А справедливее, чем в точке Б (рис. 24.1). [c.585]
Кривая точек возможной полезности [c.321]
КРИВАЯ ТОЧЕК ВОЗМОЖНОЙ ПОЛЕЗНОСТИ — геометрически местонахождение точек возможной полезности [c.321]
Анализ кривой безразличия позволяет выразить графически предпочтения потребителя. Анализ строится на предположении, что потребители могут ранжировать возможные альтернативы. Но потребительские предпочтения можно также описать, используя концепции полезности и предельной полезности. Мы рассмотрим эти концепции и их связь с анализом кривых безразличия. [c.92]
Рассмотрим движение от точки А к точке Е. Это движение нельзя оценить при помощи критерия Парето. ZZ есть кривая возможной полезности, проходящая через точку Е. Заметим, что имеются и другие точки (например, F и G), к которым можно перейти из Е путем перераспределения богатства. Эти точки лежат выше точки А. По критерию Калдора, движение от точки А к точке Е является улучшением, так как в точке Е можно таким образом перераспределить богатство, что в результате изменения никто не понесет убытков. (Видно, что убыток, который несет Федор, компенсирован в точке G и особенно в точке F). Подводя итоги, отметим, что движение от точки А к точке Е является улучше- [c.195]
Двойной критерий Т. Сцитовски. Американский экономист Т. Сцитов-ски заметил, что критерий, предложенный Калдором, имеет серьезные недостатки. По этому критерию, возможно, что движение от точки А к точке Н (рис. 9.6, в) означает, что возможно улучшения положение, но в то же время движение от Н к А будет также улучшением. Точка А лежит ниже кривой возможной полезности ZZ, которая проходит через точку Н, но в то же самое время Н лежит ниже кривой возможной полезности JJ, проходящей через точку А. (Такая ситуация возникает в случае пересечения двух кривых возможной полезности.) [c.196]
Заметим, что если кривые возможной полезности никогда не пересекаются, то может возникнуть следующая проблема. В точке J (рис. 9.6, г) положение Федора лучше, а положение Трифона хуже, чем в точке А. Если по критерию Калдора и Сцитовски положение в точке J лучше, чем в точке А, поскольку кривая возможной полезности, проходящей через J, лежит выше А, то нет однозначного повода для такого заключения. [c.196]
Во-первых, мы не можем проранжировать состояния на кривой возможных полезностей, т. е. расставить по степени предпочтения различные парето-эф-фективные состояния. Обращаясь к рис. 1, можно сказать, что критерий Парето не дает нам оснований утверждать, какая из точек F, A, D, С, F лучше . Отсюда следует вывод, что критерий Парето нейтрален по отношению к распределению полезностей между индивидами. В точке F Борис получает все, а Андрей — ничего, в точке F — наоборот, и тем не менее оба случая относятся к парето-эффективным состояниям. О них можно говорить как о парето-несравни-мых состояниях. [c.250]
Во-вторых, не всегда критерий Парето позволяет характеризовать переход от парето-неэффективного к парето-эффективному состоянию как парето-улучше-ние и соответственно обратный переход как парето-ухудшение. Возьмем, например, переход из точки G в точку Е на рис. 1. Точка Е находится на кривой возможных полезностей, следовательно, характеризует парето-эффективное состояние. Точка G, как мы знаем, нет. И тем не менее этот переход не является парето-улучшением. Относительно точки G любые возмож- [c.250]
| Рис. 4. Кривая возможных полезно-стей. | 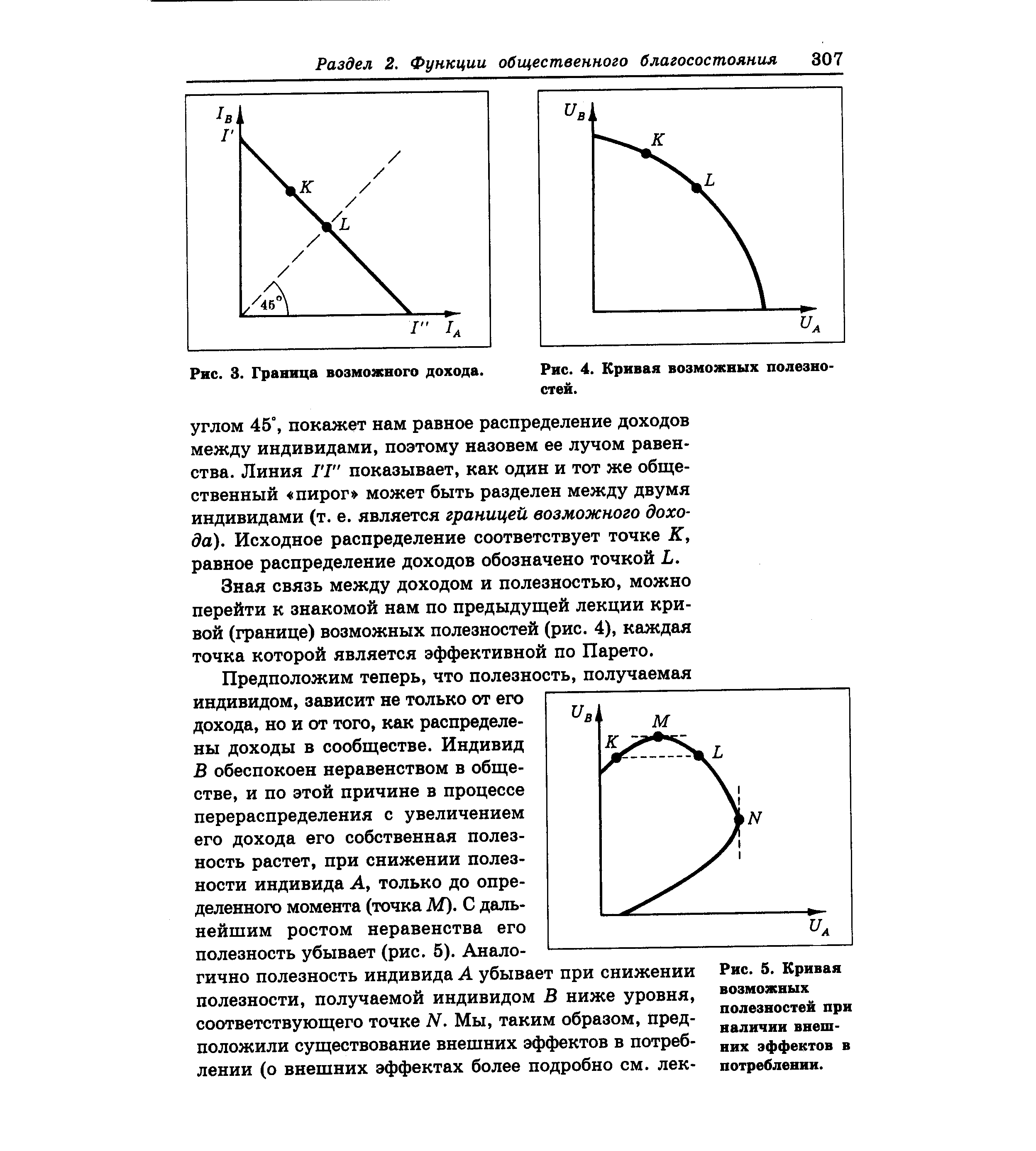 |
В этой работе делается попытка провести грубый эмпирический тест путем объединения нескольких общих наблюдений поведения людей при выборе среди альтернатив, предполагающих риск, и путем исследования, согласуются ли эти наблюдения с гипотезой, возрожденной фон Нейманом и Моргекштерном (части 3 и 4). Оказывается, что эти эмпирические наблюдения полностью согласуются с гипотезой, если кривой совокупной полезности денег придается довольно своеобразная форма (часть 4). Эта особая форма, которой может быть дано вполне удовлетворительное объяснение (часть 5), не только относит к рациональной максимизации полезности многое из того в поведении людей, что обычно объясняется другими подходами, но также касается наблюдаемого поведения, неиспользованного при получении этой кривой (часть 6). Дальнейшая эмпирическая проверка сделает возможным определить, сообразуется ли это с реальностью или нет. [c.213]
Эти соображения представлены на рис. 10.6 траекториями KSG и K S G. Когда процентная ставка относительно высока, существует KSG когда же она сравнительно низка, действует K S G. KSG во всех точках расположена снаружи K S G, так как, при прочих равных условиях, чем выше процентная ставка, тем больше чистая прибыльность данного портфеля (поскольку определенный портфель обусловливает определенный объем сделок с облигациями, а следовательно, и определенный объем издержек). Если ставка процента составляет, скажем, г]( то в этом случае будет существовать траектория KSG, характеризующая соотношение ожидаемой прибыльности портфеля и средней доли денежных остатков в нем. Это показывает, что в портфеле кажется такая доля денег (А//ИО (или облигаций [/ — (М/Й )]), ПРИ которой Hw максимизирована. Если средний объем денежной наличности больше (M/W)1, брокерская комиссия, обусловленная хранением меньшего среднего количества облигаций, снизится, но это сокращение будет меньше снижения процентных поступлений. Если же средние денежные остатки меньше, чем (A / 0, брокерская комиссия увеличится в большей степени, чем процентные поступления 1. Результатом этого (и линии LV в части С) является то, что траектория возможностей в части А на рис. 10.6 образует отрезок OF на горизонтальной оси. Индивид максимизирует полезность в точке F и, находясь в этой точке, будет хранить средний остаток денег (Л /ЙО1. Но если процентная ставка снизится до г, вместо кривой K1S1Gt образуется кривая K2S2G2. При любой заданной доле денег в портфеле доход от портфеля будет меньшим, чем в предыдущем случае. Кривая возможностей в части А образует OF, и максимизирующий полезность средний объем денежной наличности достигнет (M/W)2. [c.350]
Интегрированная модель, объединяющая три допущения, каждое из которых в отдельности предполагает возникновение эластичного по проценту спроса на деньги (ожидаемое изменение процентных ставок, неуверенность относительно будущих процентных ставок и трансакци-онные издержки), представлена на рис. 11.2. В части С положение LN соответствует допущению о том, что риск портфеля возрастает как линейная функция изменения доли облигаций в портфеле. В части В снова появляются два возможных положения кривой. Если ожидаемый уровень будущей процентной ставки окажется таким, что г, < г , то будет существовать траектория K G,. Если же ожидания сведутся к г, > г , то возникнет K2SGl. Объединив траектории в частях В и С, мы получим кривую возможностей в части А. При г < г она займет место PF и лицо будет максимизировать полезность, имея недиверсифицированный портфель (М/М + В= 1). В этом случае может возникнуть ликвидная ловушка. Если же /-j > г , эта кривая займет положение FZF и равновесие будет достигнуто, скажем, в точке Е. Лишь отрезок FZ траектории FZF имеет отношение к принятию решений о структуре портфеля. Лицо, стремящееся избежать [c.369]
