Как мы уже говорили в предыдущем параграфе, множество, описываемое системой (4.23), (4.24), является выпуклым и многогранным. В связи с линейностью критерия (4.22) можно утверждать, что решение задачи (если, конечно, оно существует) достигается па границе множества допустимых решений (4.23), (4.24), его выпуклость гарантирует, что найденный локальный максимум будет совпадать с глобальным. Поскольку это множество является многогранным, то из линейности критерия следует, что решение достигается в вершине множества. Если решение задачи (4.22) —(4.24) не единственно (например, целая грань множества), то среди решений хотя бы одно является вершиной. На этом. факте основано большинство методов решения задач линейного программирования. [c.50]
Методы выявления предпочтений ЛПР до рассмотрения множества допустимых решений обычно опираются на взвешивание различных критериев либо в виде (3.9) с априорным назначением весов, либо с помощью других методов свертывания критериев, рассмотренных ранее. При этом, конечно, критерии должны быть количественными целевыми функциями. Иногда используются-также методы диалогового построения функций полезности (или кривых безразличия). Отметим, что в рассматриваемых задачах заранее известны допустимые варианты решения, поэтому разумно использовать их и решать проблему выявления предпочтения одновременно с выбором решения задачи. Рассмотрим такие методы более подробно. [c.319]
Определение ограничений так же, как и целей может производиться качественно и количественно. Методика их формирования во многом аналогична методике формирования целей. Анализ ограничений на этапе формирования альтернатив решения позволяет исключить варианты, не обеспеченные ресурсами или не удовлетворяющие другим ограничениям, из дальнейшего рассмотрения и сузить общее множество возможных альтернатив до множества допустимых решений (допустимых альтернатив). [c.186]
Любой набор переменных решения, удовлетворяющих этим ограничениям, мы будем называть допустимым решением (или допустимым планом). Обычно существует множество допустимых решений. Разумеется, каждому из них отвечает свое (не обязательно оптимальное) значение целевой функции. [c.27]
Все эффективные решения между собой несравнимы, т. е. нельзя сказать, какое из них предпочтительнее. В частных случаях множество эффективных решений может содержать только одно решение или совпадать с множеством допустимых решений. В первом случае единственное решение является оптимальным, а во втором случае сужения допустимого не произошло. Непосредственно из определения эф- [c.572]
Понятие М. используется в геометрической интерпретации задач линейного программирования множество допустимых решений задачи является выпуклым М., базисное решение или опорный план — одной из его вершин. (См. Вершина допустимого многогранника). [c.198]
МНОЖЕСТВО ДОПУСТИМЫХ РЕШЕНИЙ [c.202]
В зависимости от вида используемых критериев оптимальности целевых функций или функционалов) и ограничений модели (множества допустимых решений) различают скалярную О., векторную О., многокритериальную О., стохастическую О. (см. Стохастическое программирование), гладкую и негладкую (см. Гладкая функция), дискретную и непрерывную (см. Дискретность, Непрерывность), выпуклую и вогнутую (см. Выпуклость, вогнутость) и др. Численные методы О., т.е. методы построения алгоритмов нахождения оптимальных значений целевых функций и соответствующих точек области допустимых значений,—развитый отдел современной вычислительной математики. См. Оптимальная задача. [c.247]
Множество допустимых решений 202 [c.474]
Под экстремальной задачей понимают задачу о максимуме некоторого критерия 1(х) на множестве допустимых решений х Е D [c.311]
Понятие тождественности экстремальных задач можно обобщить на случай, когда множества допустимых решений исходной и преобразованной задач различны. Рассмотрим две задачи. [c.313]
Функция /о непрерывна и ограничена на [а, 6]. Если ввести соответствие между множествами допустимых решений этих задач, при котором решению х° задачи А соответствует решение 6(х° — г) в задаче А1, то они окажутся тождественными относительно решения в смысле данного выше определения. [c.313]
Расширение экстремальных задач. Ниже часто будет использован прием, при котором исходная экстремальная задача заменяется другой задачей — с более широким множеством допустимых решений. [c.313]
Множества допустимых решений задач (9.17), (9.19) не принадлежат пространству Rn, тем не менее согласно определению расширения, приведенному выше, каждая из задач (9.17),(9.19) является расширением для задачи (9.16). [c.317]
Каждому вектору XQ E D соответствует распределение вида Р 0(х) (9.22) и обратно, причем значения f(x] в (9.16), f(x] в (9.17) и f(x] в (9.19) на соответствующих элементах решений совпадают, так что задача (9.16) эквивалентна задачам (9.17), (9.19), в которых множество допустимых решений ограничено решениями, имеющими вид (9.22), а х берется из множества D. [c.318]
Функция Лагранжа. Пусть х — элемент множества допустимых решений D такой, что значение /о( ) не меньше значения /о для любого другого элемента L>, т.е. х — оптимальное решение задачи НП. Выясним, каким условиям кроме неравенства [c.330]
Отметим, что если в задаче НП требовалось бы найти не максимум, а минимум /о (а ) на том же множестве допустимых решений, то условия (9.72), (9.73), определяющие х и Л, не изменились бы, так как при выводе необходимых условий минимума в неравенствах (9.69) фигурировал бы знак >, однако для внутренней точки D такое неравенство переписывается как равенство, т.е. принимает вид (9.70), что и приводит к условиям (9.72). Это не удивительно потому, что для задачи о безусловном максимуме и минимуме дифференцируемой функции необходимые условия оптимальности совпадают. [c.332]
Выясним, как связан характер функции достижимости с поведением целевой функции /о(а ) и функций, определяющих множество допустимых решений. Рассмотрим задачу [c.339]
Расширение с использованием штрафных функций. Расширение для задачи нелинейного программирования образуется с использованием штрафной функции Ф(а,а ) множества допустимых решений этой задачи как [c.351]
При этих условиях параметры А и структуру R желательно выбирать так, чтобы максимум а (А) в задаче (9.121) оказался на множестве допустимых решений задачи (9.120), т.е. были выполнены условия /(а (А )) = 0. Это возможно, если функция достижимости R (С А) задачи [c.356]
Таким образом, на множестве допустимых решений расширенной задачи нужно наложить дополнительные ограничения, выделив из всех возможных распределений только ( -образные, чтобы получить задачу, тождественную исходной. Следовательно, НП является расширением для задачи НП (см. п. 9.2). [c.366]
| Рис. 9.17. Функция достижимости и ее выпуклая оболочка для случая, когда множество допустимых решений исходной задачи НП пусто | 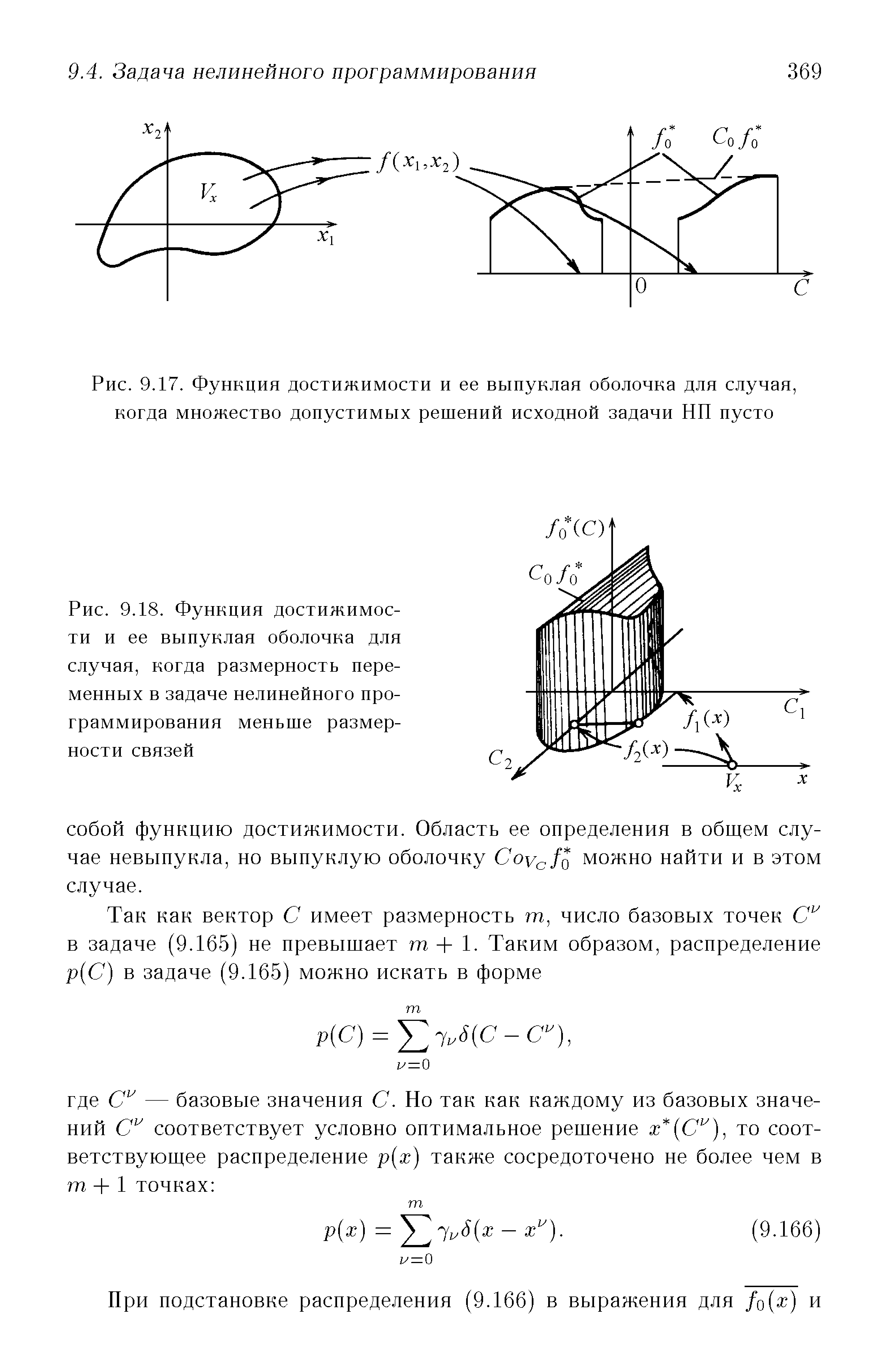 |
Формы условий, определяющих множество допустимых решений. Условия, определяющие множество допустимых решений, могут иметь как форму равенств, так и форму неравенств. Ниже для краткости мы будем записывать только равенства. [c.377]
Здесь нами построена последовательность вершип x(l x(z х(3) таких, что каждые два соседних элемента последовательности являются соседними вершинами множества допустимых решений, причем при движении вдоль последовательности значение критерия возрастает. В последней точке достигается максимум. Подобные методы, основанные на последовательном переходе от одной вершины к другой, соседней с большим (или в крайнем случае не меньшим) значением критерия, получили название методов последовательного улучшения допустимого решения. Их использование определяется следующими преимуществами. Во-первых, переход в соседнюю вершину требует значительно меньшего объема вычислений, чем поиск некоторой [c.52]
Методы второй группы направлены на.то, чтобы дать человеку представление об эффективном множестве в целом. Далее, человек может сам выбрать то эффективное решение, которое устраивает его в наибольшей степени. Надо сказать, что в том случае, когда число показателей превышает два, эта задача является весьма сложной. Она усугубляется тем, что даже для линейных задач множество эффективных точек является певыпуклым. Для систем с выпуклыми множествами допустимых решений п линейными показателями эту трудность можно преодолеть, если дать представление о всем множестве достижимых значений показателей. В указанном случае это множество является выпуклым, поэтому его структуру можно понять па основе анализа различных двумерных сечений этого множества. Заметим, что при этом одновременно дается представление о структуре эффективного множества, которое является частью границы множества достижимых показателей. [c.61]
Принятие решения в автоматизированной системе организационного управления, как правило, осуществляется специалистом с применением или без применения технических средств, но в последнем случае на основе тщательного анализа результатной информации, полученной на ПЭВМ. Задача принятия решений осложняется тем, что специалисту лриходится искать из множества допустимых решений наиболее приемлемое, сводящее к минимуму потери ресурсов (временных, трудовых, материальных и т.д.). Благодаря применению персональных ЭВМ и терминальных устройств повышается аналитичность обрабатываемых сведений, а также [c.48]
Здесь t - число этапов хт = (x,, X2,. . . , XT) - вектор переменных (план) <лт = (со,, j2>.. ., ыг) - вектор случайных событий M t pt(xt, ы ) ш 1 -условное математическое ожидание случайной вектор-функции
Однако целевой и затратный принципы эффективного решения, по мнению многих авторов2, не являются единственными критериями определения эффективности управленческого решения (рис. 12.42). Эти авторы считают, что в реальных задачах принятия решений к этапу выбора все еще сохраняется большая неопределенность информации, обусловленная наличием многих ситуаций и целей. Поэтому сразу осуществить выбор единственного решения из множества сформулированных очень сложно. В связи с этим используется принцип последовательного уменьшения неопределенности, заключающийся в последовательном сужении множества решений (альтернатив). Множество альтернативных решений сужается до множества допустимых решений на основе учета ограничений. Приемлемыми, или допустимыми, называются решения, удовлетворяющие множеству ограничений. Процедура получения множества приемлемых решений из исходного множества может выполняться путем логического мышления или формально, в зависимости от степени формализации информации. [c.572]
ВЕРШИНА ДОПУСТИМОГО МНОГОГРАННИКА [ orner point] (области допустимых решений в задачах линейного программирования) — точка пересечения линейных ограничений (напр., на рис. Л. 1 к ст. "Линейное программирование"). Поскольку множество допустимых решений в задаче линейного программирования всегда выпукло, вершинная точка является крайней точкой множества, и она может быть принята за допустимое базисное решение задачи. [c.47]
Формально З.п. состоит в нахождении лучших плановых решений из множества допустимых решений. Подробнее (применительно к практике автоматизированных систем /ыановых расчетов) это общее понятие конкретизировано в ст. "Планово-экономическая задача ". [c.102]
Менеджер должен владеть обширной информацией о тех пара метрах, которые могут быть изменены им в плановом периоде. Эт] переменные являются центральными величинами активных дейст вий менеджера. Он может представлять как независимые альтер нативы при принятии соответствующих управленческих решений Все множество допустимых решений составляет свободное про странство возможных действий, так называемую область допустимы, значений. [c.7]
Задача, тождественная (9.81) относительно решения, может быть получена посредством замены /о (а ) на Л(/о(а ), /(а ), Л), если для почти всех х фукнция R монотонно возрастает по /о на множестве допустимых решений исходной задачи. Преобразованная задача примет вид [c.336]
Заметим, что множество допустимых решений задачи нелинейного программирования (9.81) может быть пусто, т.е. внутри Vx, например, нет элементов, для которых fi(x) равнялись бы нулю. При этом функция /о (С) не определена в точке С = 0. Однако для построения ova/Q множество V дополняют до его выпуклой оболочки, и на дополнительных участках / (С) считают достаточно малой. При этом oy /Q на этих участках определена. На рис. 9.17 приведен пример функции достижимости и ее выпуклой оболочки. Решение исходной задачи отсутствует, так как для любого х Е Vx функция / не равна нулю. Усредненная задача имеет решение, которому соответствует значение целевой функции, равное " v /g(0). [c.368]
В прикладных задачах могут встречаться разнообразные сочетания типов критериев оптимальности и условий, определяющих множество допустимых решений. Математическая модель обьекта может уточняться в ходе решения, при этом меняются не только параметры, но и структура ограничений. Необходимые условия оптимальности в форме принципа максимума для задачи в канонической записи (см. параграф 9.3) позволяют получить расчетные соотношения, выделяющие оптимальное решение задачи с произвольным сочетанием критерия оптимальности и ограничений. Здесь мы приведем различные типы условий и критериев оптимальности в задачах управления со скалярным аргументом t и дадим вытекающее из теоремы 9.2 правило получения соотношений, представляющих собой необходимые условия оптимальности этих задач. [c.376]
