КОЭФФИЦИЕНТ КОНЦЕНТРАЦИИ ДОХОДОВ (Индекс Джини) — показатель, характеризующий уровень неравенства доходов устанавливает величину отклонения фактического распределения доходов населения (кривая Лоренца) от линии их равномерного распределения. [c.145]
КРИВАЯ ЛОРЕНЦА — графический показатель, характеризующий реальное распределение доходов в условиях рыночной экономики. [c.146]
Кривая Лоренца представляет собой кумулятивное распределение численности населения и соответствующих этой численности доходов. Она показывает соотношение процентов всех доходов и процентов всех их получателей. Если бы доходы распределялись равномерно, т.е. 10% получателей имели бы десятую часть доходов, 50% — половину и т.д., то такое распределение имело бы вид диагонали квадрата со сторонами от 0% до 100%. Неравномерное же распределение характеризуется кривой, отстоящей от прямой тем дальше, чем больше дифференциация. [c.662]
По горизонтали указаны процентные группы населения, а по вертикали — проценты дохода, получаемые этими группами. Если бы существовало абсолютное равенство, то 20% населения получали бы 20% всего дохода общества, 30% населения — 30% всего дохода, 40% населения — 40% дохода и т.д. Появилась бы линия ОА, которая означала бы абсолютное равенство в распределении доходов. В жизни распределение осуществляется иначе. Например, 10% населения получают 50% всех доходов, 50% населения — 20% и т.д. В этой ситуации на графике возникает кривая ОСА, которая называется кривой Лоренца. Чем дальше эта кривая от прямой ОА, тем больше различие в доходах членов общества. Степень дифференциации дохода определяется с помощью коэффициента Джини. Чем больше величина этого показателя, тем больше отклонение фактического распределения доходов от идеального равенства. Рассчитывается он путем деления площади ОСА на площадь треугольника ОАВ. [c.188]
Степень неравенства доходов можно увидеть на кривой Лоренца, приведенной на рис. 34-1. Данные о доле семей расположены на оси абсцисс, доле дохода - на оси ординат. Теоретическая возможность абсолютно равного распределения дохода представлена биссектрисой, она указывает на то, что любой данный процент семей получает соответствующий процент доходов. Это значит, что если 20% всех семей получают 20% от всего дохода, 40% получают 40%, а 60% получают 60% и т.д., то соответствующие точки будут расположены на биссектрисе. [c.748]
Нанеся на график данные за 1993 г. из табл. 34-2, мы получим кривую Лоренца, демонстрирующую фактическое распределение доходов. Как показывает точка а, 20% всех семей с самыми низкими доходами получили 4,1% дохода точка Ь показывает, что 40% семей с низкими доходами получи- [c.748]
Кривая Лоренца I [фактическое распределение) [c.748]
| Рисунок 34-1. Кривая Лоренца | 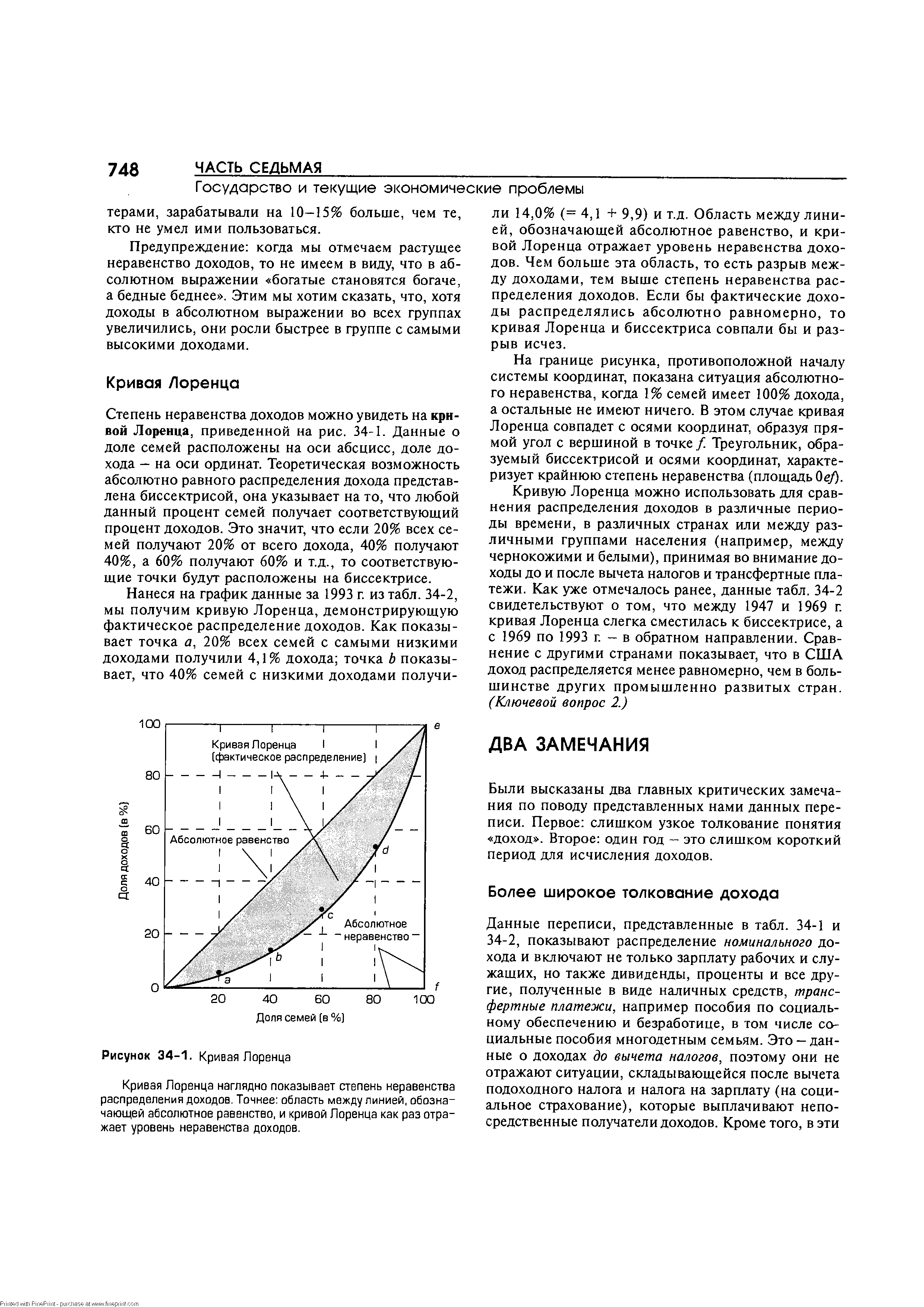 |
На границе рисунка, противоположной началу системы координат, показана ситуация абсолютного неравенства, когда 1% семей имеет 100% дохода, а остальные не имеют ничего. В этом случае кривая Лоренца совпадет с осями координат, образуя прямой угол с вершиной в точке / Треугольник, образуемый биссектрисой и осями координат, характеризует крайнюю степень неравенства (площадь Qef). [c.748]
Кривую Лоренца можно использовать для сравнения распределения доходов в различные периоды времени, в различных странах или между различными группами населения (например, между чернокожими и белыми), принимая во внимание доходы до и после вычета налогов и трансфертные платежи. Как уже отмечалось ранее, данные табл. 34-2 свидетельствуют о том, что между 1947 и 1969 г. кривая Лоренца слегка сместилась к биссектрисе, а с 1969 по 1993 г. — в обратном направлении. Сравнение с другими странами показывает, что в США доход распределяется менее равномерно, чем в большинстве других промышленно развитых стран. (Ключевой вопрос 2.) [c.748]
Кривая Лоренца графически отражает неравенство доходов. [c.752]
Для Соединенных Штатов характерно значительное неравенство в распределении личного дохода. Кривая Лоренца графически показывает степень этого неравенства. [c.763]
Ключевой вопрос. Предположим, что Ал, Бети, Кэрол, Дэвид и Эд получают доходы в размере 500, 250, 125, 75 и 50 дол. соответственно. Постройте кривую Лоренца для экономики, состоящей из пяти человек, и дайте необходимые пояснения. Какую долю общих доходов получают самые бедные и самые богатые [c.764]
Неравенство в распределении графически изображается с помощью кривой Лоренца (рис. 17.5.) [c.456]
Кривая Лоренца характеризует степень реально достигнутого неравенства в распределении дохода среди семей (40% семей получает 20% дохода, 60% семей — 40% всего дохода и т.д.). [c.457]
Интерес представляет также изучение распределения общей суммы доходов между различными группами населения. Например, можно поставить вопрос о том, какова доля определенной группы населения в общей сумме доходов, или о том, какая часть населения обладает некоторой заданной долей суммарных доходов. Такая постановка задачи позволяет проанализировать степень концентрации доходов у различных групп населения и количественно оценить неравномерность их распределения. Инструментом анализа является кривая Лоренца и исчисляемые на ее основе индекс концентрации доходов (коэффициент Джини) и коэффициент фондов. [c.361]
Кривая Лоренца устанавливает соответствие между численностью населения и объемом получаемого суммарного дохода. Для ее построения население разбивается на группы, равные по численности и отличающиеся уровнем среднедушевого дохода. Группы ранжируются по величине среднедушевого дохода. Для каждой выделенной группы определяются частости — доли в общей численности населения и в общей сумме доходов, а на их основе — накопленные частости. В прямоугольной системе координат на оси абсцисс откладывают накопленные частости групп по численности населения, а на оси ординат — исчисленные нарастающим итогом доли суммарного дохода. При равномерном распределении доходов десятая часть населения с самыми низкими доходами будет иметь 10% общей суммы доходов, двадцатая часть населения — 20% общей суммы доходов и т.д. На рис. 22.2 равномерное распределение доходов представлено прямой, которая соединяет начало координат А и точку С, [c.361]
Пример 22.4. Используя данные предыдущего примера, построим кривую Лоренца. Для этого выделим пять групп, равных по численности, и определим их долю в суммарном доходе. Результаты вспомогательных расчетов представим в табл. 22.6. [c.362]
Построим кривую Лоренца, дающую наглядное представление о неравномерности распределения доходов в обществе (рис. 22.2) [c.364]
Поданным задачи 21 постройте кривую Лоренца. [c.373]
Исходя из распределения дохода по его величине, можно построить кривую, которую называют кривой Лоренца, позволяющую судить об уровне неравенства. Рассмотрим построение указанной кривой. С этой целью отложим по горизонтальной оси процент семей, располагающих определенным уровнем дохода, а по вертикальной — долю совокупного дохода, приходящегося на соответствующую часть семей. [c.293]
Каждая точка кривой Лоренца показывает, какую долю в суммарном доходе имеет то или иное число семей с определенным уровнем дохода. Например, на долю 50% населения с наименьшим уровнем дохода приходилось 23% совокупного дохода. Если бы в распределении дохода наблюдалось равенство, то 20% семей с низшим уровнем дохода, получали бы 20% совокупного дохода, а каждая последующая группа семей располагала (1/5) совокупного дохода. В атом случае кривая Лоренца совпала бы с прямой (К). Заштрихованная область (М) между кривыми (L) и прямой (К) отражает уровень неравенства в распределении дохода. Чем дальше кривая (L) отстоит от прямой (К), то есть чем больше заштрихованная область, тем выше неравенство. [c.294]
Воспроизводящая сила природы Закон Оукена Инфляция предложения Инфляция спроса Кривая Лоренца [c.306]
Проиллюстрируйте графически наиболее важные точки кривой Лоренца. [c.307]
Кривая Лоренца для чистых активов [c.164]
| Рис. 8. Сдвиг кривой Лоренца в России с 1991 по 1999 г. | 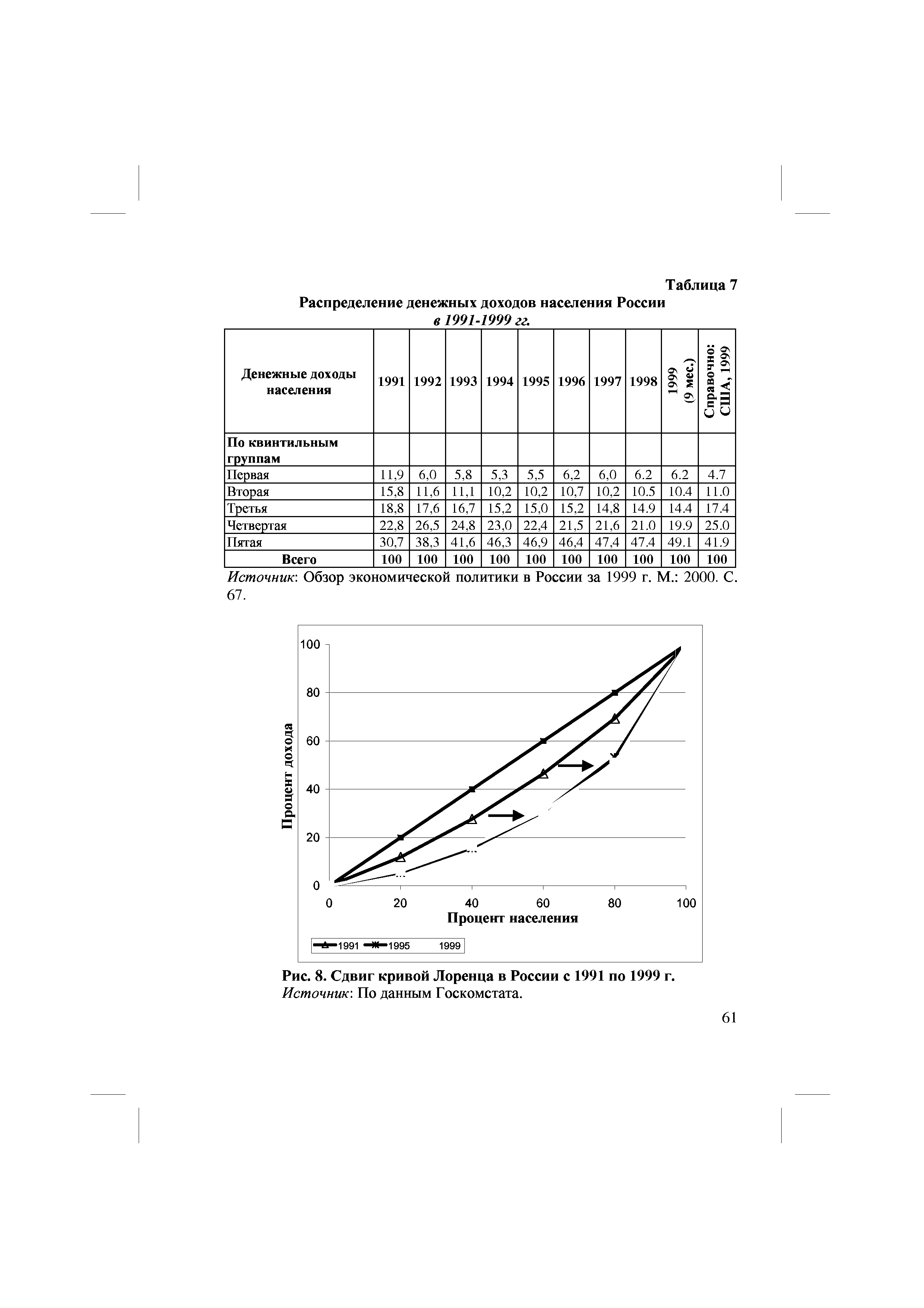 |
Кривая Лоренца после вычета напогов и трансфертных платежей [c.750]
Кривая Лоренца (Lorenz urve) — кривая, которую можно использовать для иллюстрации распределения дохода в экономике когда данную кривую используют с этой целью, суммарный процент семей (получателей доходов) измеряется по оси абсцисс, а суммарный процент доходов — по оси ординат. [c.945]
На основе данных кривой Лоренца определяется так называемый децильный (лат. de em — десять) коэффициент. Этот коэффициент показывает, во сколько раз 10% самых богатых семей превосходят по уровню дохода 10% самых бедных. [c.457]
Линия фактического распределеня доходов (кривая Лоренца) [c.362]
Смотреть страницы где упоминается термин Кривая Лоренца
: [c.121] [c.748] [c.748] [c.764] [c.457] [c.457] [c.362] [c.364] [c.294] [c.294] [c.295] [c.147] [c.62] [c.64]Смотреть главы в:
Экономикс Принципы, проблемы и политика Изд.13 -> Кривая Лоренца
Курс экономической теории Изд5 (2006) -- [ c.24 ]
Большая экономическая энциклопедия (2007) -- [ c.320 , c.367 ]
