| Рис. 1. Кривая Лоренца и коэффициент Джини для рынка А. | 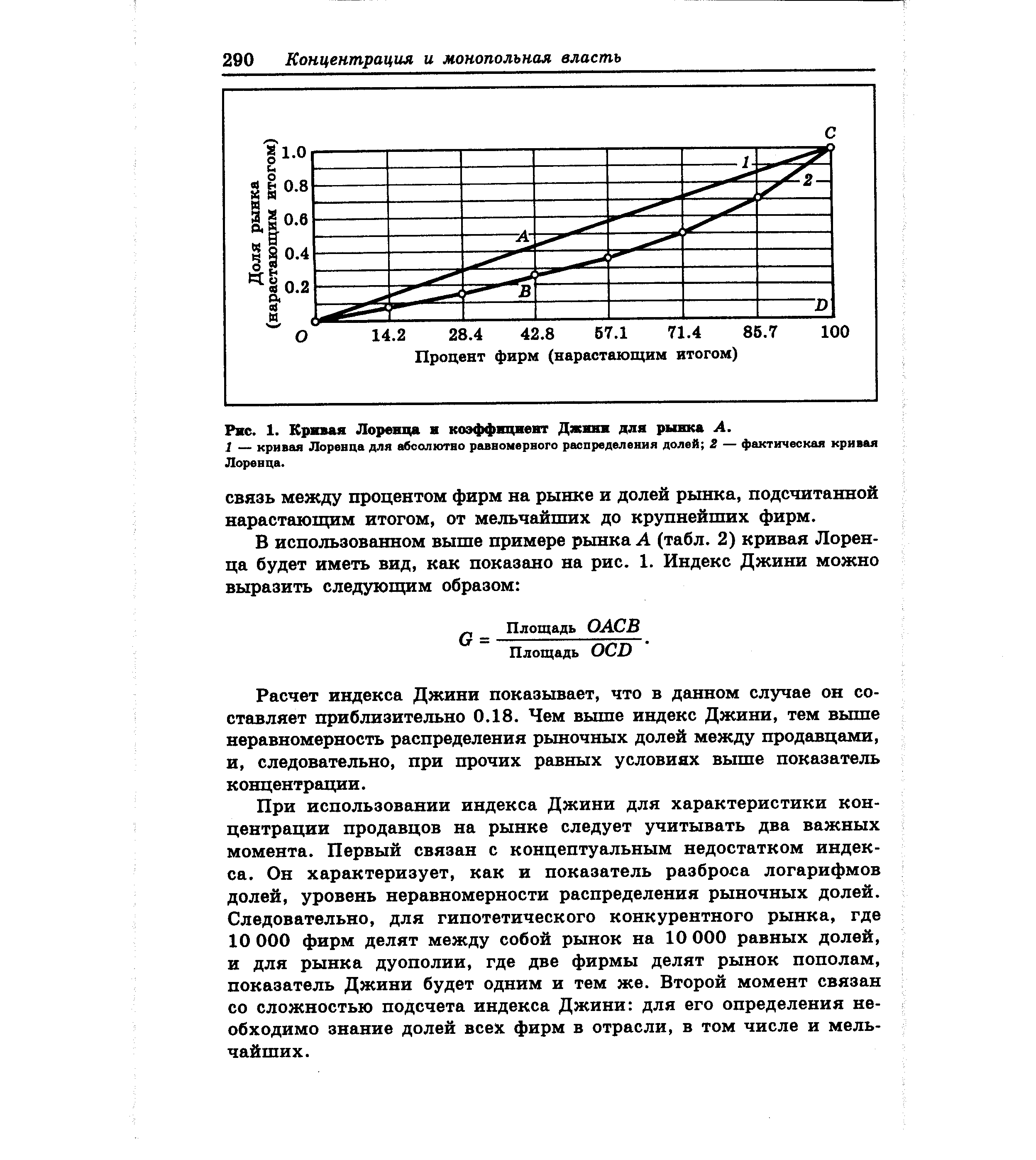 |
При изложении данного вопроса необходимо четко определить условия построения кривой Лоренца и коэффициента Джини , раскрыть их экономический смысл, указать, при каких условиях кривая может смещаться, и в завершение можно указать на основные факторы, влияющие на неравенство в распределении доходов. [c.70]
Анализировать кривую Лоренца и коэффициент Джини. [c.390]
Дифференциация доходов различных групп населения определяет их жизненный уровень. Для определения неравенства в распределении доходов экономическая наука использует т.н. кривую Лоренца и коэффициент Джини. Суть кривой Лоренца состоит в следующем. Если предположить абсолютное равенство в доходах (10% населения получают 10% всех доходов, 20% населения - 20% всех доходов и т.д.), то на графике это будет представлено в виде прямой ОЕ (см. рис. 6-1). [c.72]
Проблема измерения неравенства в распределении доходов кривая Лоренца и коэффициент Джини [c.592]
Рыночное, пофакторное распределение доходов не обеспечивает равенства доходов. Степень неравенства в распределении доходов характеризует кривая Лоренца и коэффициент Джини. Чем больше значение коэффициента Джини, тем больше неравенство в доходах общества. В современных условиях негативные стороны рынка смягчаются государством. [c.181]
Другим показателем степени неравенства является коэффициент Джини, рассчитываемый на основе кривой Лоренца. Для построения кривой Лоренца по оси абсцисс откладывается накопленная процентная доля населения группы стран или регионов с доходами ниже определенного уровня, тогда как по оси ординат - накопленная доля дохода стран в общем доходе по выборке. При построении кривой все страны ранжируются в порядке возрастания уровня дохода в расчете на душу населения. На основе построенной таким образом кривой Лоренца рассчитывается коэффициент Джини, представляющий собой отношение площади между кривой и прямой, проведенной под углом 45°, ко всей площади под прямой, проведенной под углом 45°. Аналитическое выражение для расчета коэффициента Джини имеет следующий вид [c.41]
Интерес представляет также изучение распределения общей суммы доходов между различными группами населения. Например, можно поставить вопрос о том, какова доля определенной группы населения в общей сумме доходов, или о том, какая часть населения обладает некоторой заданной долей суммарных доходов. Такая постановка задачи позволяет проанализировать степень концентрации доходов у различных групп населения и количественно оценить неравномерность их распределения. Инструментом анализа является кривая Лоренца и исчисляемые на ее основе индекс концентрации доходов (коэффициент Джини) и коэффициент фондов. [c.361]
Обратимся к данным таблицы 3, характеризующим распределение населения СССР по среднедушевому совокупному доходу в 1990 году и попробуем на основе этих данных построить кривую Лоренца и вычислить значение коэффициента Джини. Однако здесь мы сталкиваемся с некоторыми трудностями. Как [c.220]
Количественно степень неравенства в распределении доходов можно выразить с помощью коэффициента Джини. Он рассчитывается как отношение площади фигуры, образуемой биссектрисой ОК и кривой Лоренца к общей площади треугольника OKF. Из этого показателя следует чем неравномернее распределение доходов, тем сильнее прогиб кривой Лоренца и больше площадь, огибаемая этой кривой. Следовательно, коэффициент Джини будет увеличиваться, характеризуя усиление неравенства семей по уровню доходов. Например, по расчетам экономистов, в 1984 г. в США данный коэффициент равнялся 0,359, а в 1987 г. - 0,365. С учетом этого американское правительство строит свою политику в области перераспределения доходов, о чем речь пойдет далее. [c.217]
По горизонтали указаны процентные группы населения, а по вертикали — проценты дохода, получаемые этими группами. Если бы существовало абсолютное равенство, то 20% населения получали бы 20% всего дохода общества, 30% населения — 30% всего дохода, 40% населения — 40% дохода и т.д. Появилась бы линия ОА, которая означала бы абсолютное равенство в распределении доходов. В жизни распределение осуществляется иначе. Например, 10% населения получают 50% всех доходов, 50% населения — 20% и т.д. В этой ситуации на графике возникает кривая ОСА, которая называется кривой Лоренца. Чем дальше эта кривая от прямой ОА, тем больше различие в доходах членов общества. Степень дифференциации дохода определяется с помощью коэффициента Джини. Чем больше величина этого показателя, тем больше отклонение фактического распределения доходов от идеального равенства. Рассчитывается он путем деления площади ОСА на площадь треугольника ОАВ. [c.188]
Динамика этих показателей, как и кривая Лоренца, также свидетельствует об увеличении неравенства доходов в РФ в 1990-х гг. (табл.). Децильный коэффициент вырос в 1990—99 гг. более чем в 3 раза, значение индекса концентрации доходов (коэффициент Джини) повысилось с 0,289 до 0,396. Большинство исследователей, занимающихся проблемами дифференциации доходов, утверждают, что реальные масштабы неравенства в РФ намного выше, чем это показывает официальная статистика. Напр., децильный коэффициент составляет не 14,5, а, с учётом сокрытия доходов,- 23—25. Можно говорить о формировании в стране обширного слоя бедных, т. е. тех, чьи доходы ниже установленного в стране официального прожиточного минимума (в сентябре 1999 г. он равнялся 920 руб.), их доля в общей численности населения увеличилась более чем в 20 раз. [c.72]
Количественно степень неравенства в распределении доходов можно вычислить с помощью коэффициента Джини, названного по имени итальянского экономиста и статистика К. Джини (1884 — 1965). Коэффициент Джини определяется как отношение площади заштрихованной фигуры М к площади фигуры AB (рис. 7.2). Очевидно, чем больше отклонение кривой Лоренца от биссектрисы, тем больше будет площадь фигуры М, а следовательно, тем больше коэффициент Джини будет приближаться к единице. В большинстве развитых стран коэффициент Джини колеблется в пределах 0,27 — 0,33. [c.185]
Определите 1) средний размер дохода на семью 2) моду 3) медиану 4) децильный коэффициент дифференциации дохода. Постройте кривую распределения Лоренца. Определите коэффициент концентрации доходов (коэффициент Джини). Проанализируйте полученные результаты и сформулируйте выводы. [c.180]
Постройте кривые концентрации Лоренца и рассчитайте коэффициенты концентрации доходов Джини для I полугодия 1998 г. и для I полугодия 1999 г. [c.181]
Ключевые понятия общий продукт, средний продукт, предельный продукт, закон убывающей предельной отдачи, производный спрос, заработная плата, номинальная и реальная заработная плата, кривая Лоренца, коэффициент Джини, валовые инвестиции, чистые инвестиции, амортизация, процент, абсолютная рента, дифференциальная рента. [c.54]
Методы измерения неравенства в распределении доходов. Принципы социальной справедливости и функции общественного благосостояния. Кривая Лоренца. Индекс Джини (коэффициент концентрации доходов). Экономические параметры бедности. [c.129]
ЛОРЕНЦА КРИВАЯ [Lorenz urve] — графическое средство для характеристики неравенства в распределении доходов. На осях первого квадранта (рис. Л. 4) откладываются проценты населения и доходов. Тогда прямая ОА, проходящая под углом 45°, свидетельствует о полной равномерности распределения чем дальше от нее кривая ОВ А, ОБ1 А и т.д., тем оно менее равномерно. Отношение площади между прямой О А и кривой Лоренца и общей площади треугольника О АХ называется коэффициентом Джини чем оно больше, тем сильнее неравенство (см. Джини коэффициент). [c.176]
У 1 линейной функцией — биссектри-А сой ОЛ, при неравномерном — кривой вида ОБА. Коэффициентом Джини именуют отношение площади фигуры между биссектрисой QA и кривой Лоренца к площади треугольника ОАС. При коэффициенте, равном 0, налицо С полное равенство в доходах населения, [c.272]
Коэффициент Джини. Одним из часто используемых измерителей различия в распределении дохода является коэффициент Джини. Чем ближе к диагонали кривая Лоренца, тем более равномерно распределение дохода. Мы можем измерить расстояние до диагонали, через вычисление площади между кривой и диагональю14. Эта площадь, помноженная на два, и есть коэффициент Джини. Если площадь равна 0, коэффициент Джини равен 0, и нет неравенства когда площадь равна 1/2 весь доход принадлежит богатейшей части общества и коэффициент Джини равен 1. Так, коэффициент Джини должен лежать между 0 и 1. Для Соединенных Штатов и [c.264]
По сравнению с социологией, экономическая теория довольно давно занимается изучением проблем рынка труда. В экономике труда (labor e onomi s) есть специальные разделы, посвященные качеству рабочей силы и заработной плате. Традиционно неравенство при распределении доходов выражается кривой Лоренца, показывающей отклонение от равномерного распределения соотношения накопленного процента работников и накопленного процента заработков, и коэффициентом Джини, [c.46]
Обобщающий показатель неравенства получается из кривой Лоренца (Lorenz urve) и представляет собой отношение площади между этой кривой и линией абсолютного равенства к общей площади под линией абсолютного равенства. Очевидно, что коэффициент Джини имеет максимальное значение, равное единице (абсолютное неравенство), и минимальное значение, равное нулю (абсолютное равенство). Обратите внимание на то, что коэффициент Джини является относительным показателем. Кроме того, одно распределение может быть более равным, чем другое в одном диапазоне, и менее равным в другом диапазоне, при этом значение коэффициента будет для обоих распределений одинаковым. [c.204]
Обратите внимание, что коэффициент Джини менялся в меньшей степени, чем показатели, характеризующие каждую из пяти квантиль-ных долей. Последние в определенной мере взаимопогашались , так что площадь под кривой Лоренца могла и вообще оставаться неизменной, несмотря на некоторое изменение конфигурации самой кривой. [c.235]
Коэффициент Джини можно получить и более простым путем. Если разделить заштрихованную площадь (Т) на графике, который характеризует кривую Лоренца, на всю площадь треугольнака OFE, то получится доля, которая отражает степень неравенства в распределении доходов, т. е. G = Т OFE. Это отношение также характеризует степень концентрации доходов. Чем выше значение показателя, тем неравномернее распределены доходы в обществе. В России в период после 1990 г. индекс Джини увеличился с 0,260 до [c.324]
Область между линией абсолютного равенства и кривой Лоренца указывает на степень неравенства в распределении дохода. Чем больше эта степень, тем больше кривая Лоренца стоит дальше от прямой ОА и прижимается к отрезкам ОВ и АВ. Чем больше площадь фигуры OEAF, тем выше неравенство в распределении дохода (в точке В кривая Лоренца показывает абсолютное неравенство). Для измерения степени неравенства распределения дохода используют показатель коэффициент Джини — отношение площади области OEAF к площади треугольника ОАВ. Если коэффициент Джини = 1, следовательно, кривая Лоренца сместилась к точке В, а это показывает, что общество находится в состоянии абсолютного неравенства, и наоборот, если коэффициент = 0, то кривая Лоренца совпадает с прямой ОА и в обществе наблюдается абсолютное равенство в распределении доходов. [c.71]
В основе расчета коэффициента Джини, базирующегося на использовании кривой Лоренца, лежит идея, что крайними позициями в распределении доходов, или благ между группами лиц, являются эгалитарное (когда все участвующие в распределении получают равные доли) и антиэгалитарное (когда только один участник распределения получает все блага). Первый случай описывает полное равенство, а второй — абсолютное неравенство в распределении. Величина коэффициента Джини определяется на основе данных о распределении домохозяйств (населения) по уровню среднего на домохозяйство (члена домохозяйства) дохода. Вся совокупность получателей доходов делится на пять равных квинтильных групп и определяется, какой долей дохода владеет каждая группа домохозяйств (населения). Затем по полученным итогам строится кривая Лоренца (графическое изображение уровня концентрации явления). [c.318]
