Обозначим QJ - множество вершин сетевого графика, принадлежащих [c.20]
Работам соответствуют вершины сетевого графика, а зависимостям [c.79]
Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (рис. 8.1) [c.97]
На 1-й уровень помещается начальная вершина сетевого графика. На (п + 7)-й уровень помещаются все вершины графа, непосредственно связанные с уровнем (п) и соединяются с ним ребрами работ. Расположение вершин на каждом уровне осуществляется слева направо в порядке возрастания номеров. [c.33]
В маркировке вершин сетевого графика модели типа AoN помимо индекса работ используются параметры (см. Рис. 5) [c.113]
| Рисунок 5. Пример маркировки вершин сетевого графика модели типа AoN | 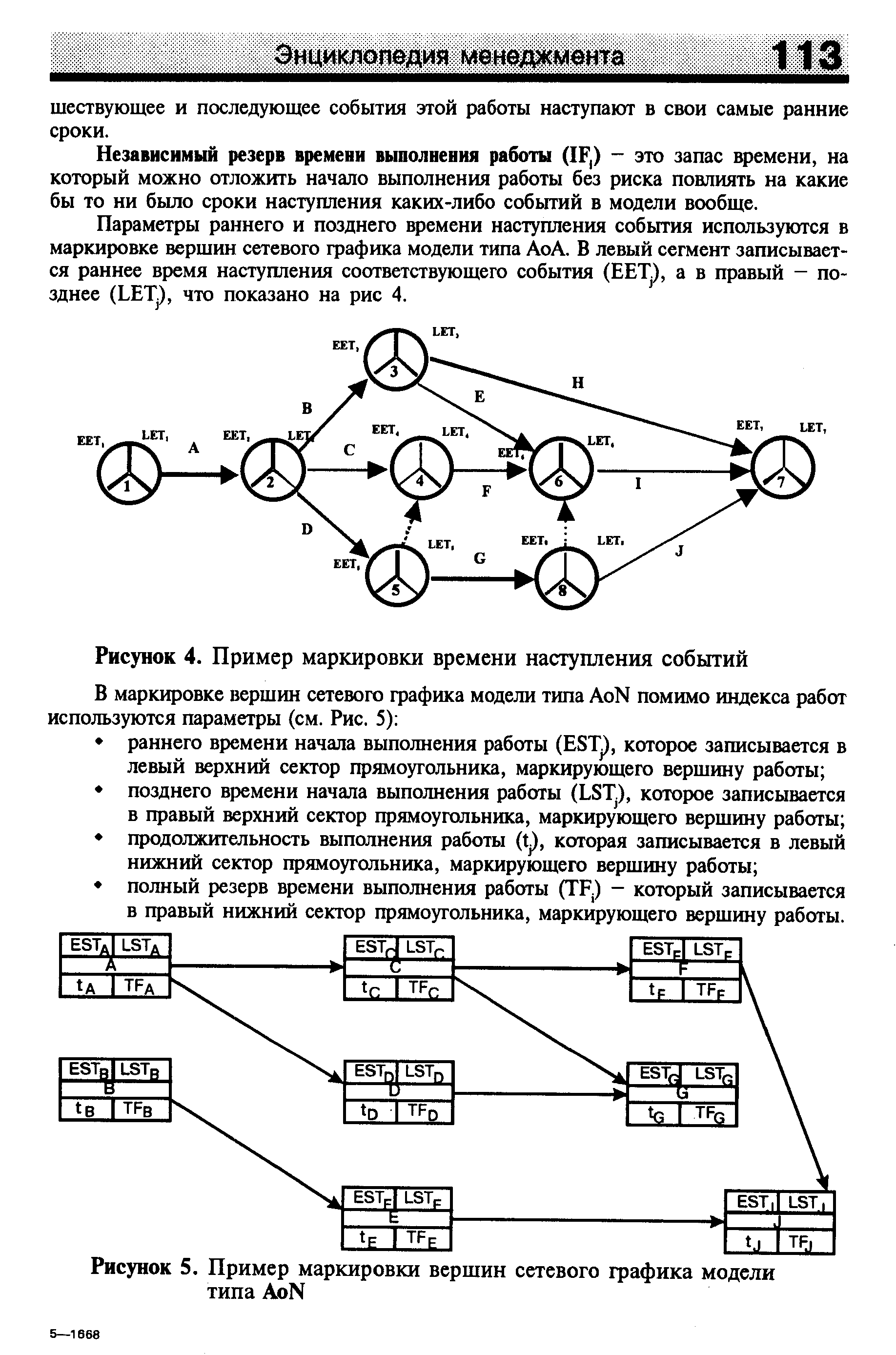 |
Ребра сетевого графика имеют одну или несколько числовых характеристик. В сетевом графике в отличие от ленточного, где основным является только один элемент — этап, как правило, имеются два основных элемента — работа и событие. Ребрами на графике изображаются работы, а вершинами — события. [c.36]
Понятие сетевой модели. Основой сетевой модели комплекса операций является сетевой график (или просто сеть), который дает наглядное представление о комплексе. Сеть состоит из множества вершин (узлов) и множества дуг (ребер, звеньев), соединяющих различные пары вершин. На каждой дуге может быть задана определенная ориентация (направление). На графике вершины сети изображаются кружками, а дуги — линиями, их соединяющими. Ориентация указывается стрелками. Каждой вершине присваивается номер i. Дуга, соединяющая вершину i с вершиной /, обозначается символом (i, j) или Рц. [c.192]
Изложенный выше способ представления комплекса работ использует язык события — операции ( события — работы ). Можно использовать другой способ представления работы — связи , в котором вершинами сети будут работы, а дуги отражают их логические связи. В таком представлении нет необходимости вводить фиктивные работы. Продемонстрируем этот прием на примере планирования научных разработок. Читатель уже знаком с основными этапами проведения модельного исследования, поэтому ему будет ясен смысл работ сетевого графика. [c.193]
Теперь после составления сети работ, которые необходимо совершить для реализации комплекса (проекта), рассмотрим некоторые из задач, возникающих при анализе сетевых- графиков. Предварительно напомним, что часто работы (дуги сети) обозначают при помощи номеров событий (вершин сети), которые они связывают. Так, работа /1 на рис. 3.6 обозначается через Р4.2, работа Б — через Pz, 3. работа В — через / 5, работа Г — через Ps. 4 и т. д. [c.195]
| Рис. 6.1. Сетевой график строительства котельной. Обозначения каждый круг считается одной из вершин графика цифра в верхнем секторе каждой вершины означает ее порядковый номер из номеров двух соседних вершин складывается шифр работы цифра в нижнем секторе каждой вершины является порядковым номером предшествующей вершины, а линия, соединяющая эти две вершины, означает определенную работу. Внизу под линией записана плановая продолжительность данной работы цифра в левом секторе каждой вершины означает общую продолжительность всех предшествующих работ, цифра в правом секторе отличается от цифры в левом на величину резерва (запаса времени). Таким образом, для вершин, лежащих на критическом пути, цифры в левом и правом секторах вершины совпадают, поскольку запас времени равен 0. | 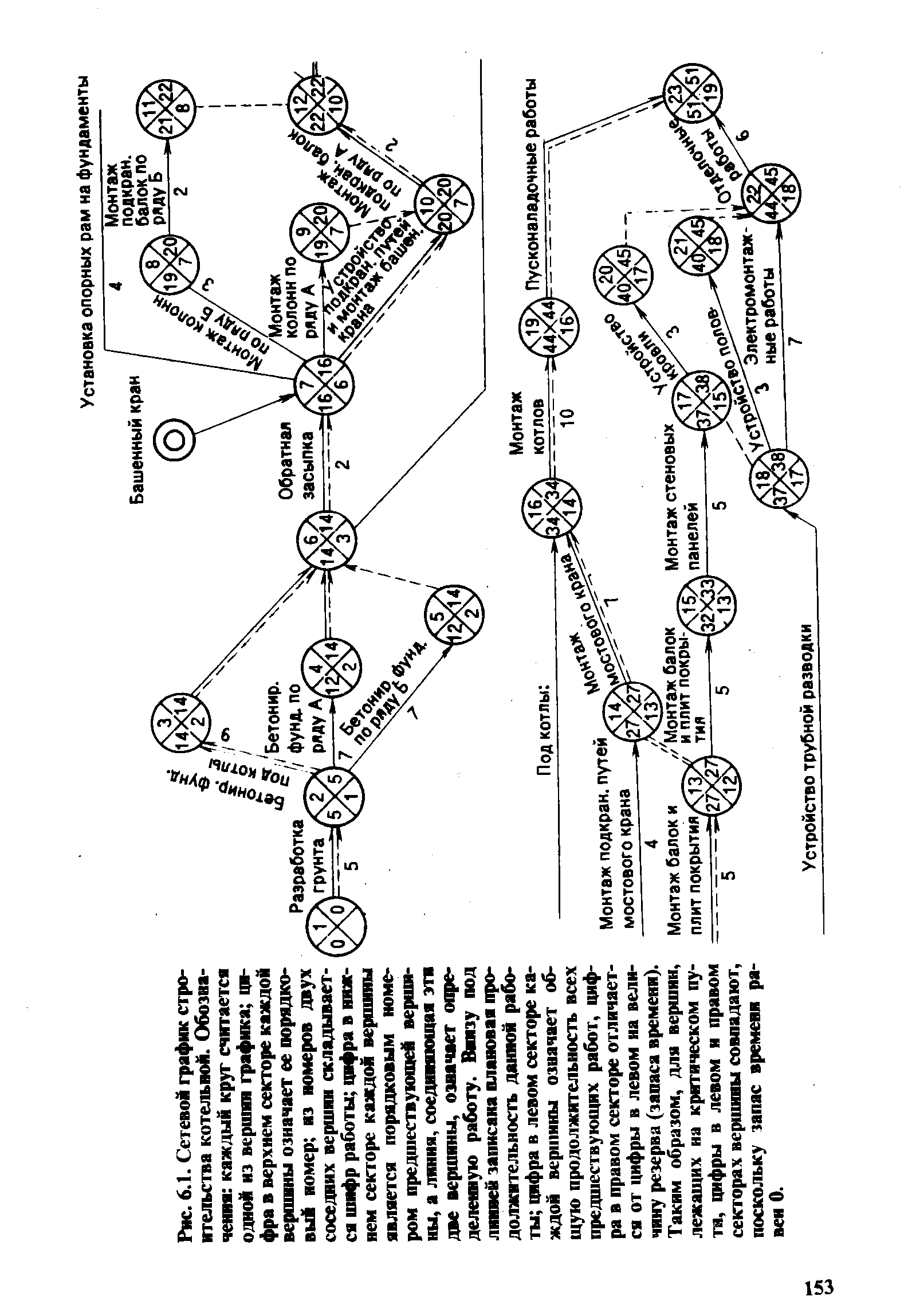 |
Пример 3.2. Пусть сетевой график ( вершина - событие ) имеет вид [c.40]
Наиболее часто в настоящее время применяются сетевые графики вида "работа-вершина" с постоянной продолжительностью работ. Для расчета временных показателей сетевых графиков в системах управления проектами применяют аппарат методов сетевого планирования и управления. [c.23]
Сетевой график — это ориентированный граф без контуров, ребра которого имеют одну длину или несколько числовых характеристик. В отличие от ленточного графика, где основным является только один элемент — работа, в сетевом графике, как правило, имеются два основных элемента — работа (изображается на графике ребром) и событие (соответствует вершине). [c.220]
Изобразив в виде сетевого графика последовательность отображенных на рис. П.2 работ, можно получить значительно лучшее представление о проекте, о взаимосвязи составляющих его работ. Этот сетевой график показан на рис. 11.3. Ребра графика помечены названиями соответствующих работ, рядом с названием проставлена продолжительность выполнения работы. Под графиком расположена ось времени, дающая представление о сроках начала и завершения любой из работ (проекции вершин графика на временную ось). [c.222]
Взаимосвязь работ и событий, необходимых для достижения конечной цели проекта, изображается с помощью сетевого графика (сетевой модели). Работы изображаются стрелками, которые соединяют вершины, изображающие события. Начало и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями. [c.87]
Все события (вершины) в сетевом графике в форме работа-стрелка должны быть пронумерованы. Предпочтительной является так называемая упорядоченная нумерация, при которой номер вершины, стоящей в начале дуги (в хвосте стрелки), будет меньше номера вершины, стоящей в конце дуги (у острия стрелки), т. е. для любой дуги i < j. Большинство алгоритмов, по которым проводятся расчеты, связанные с сетевыми графиками, ориентированы именно на упорядоченную нумерацию вершин. Упорядочение вершин может быть выполнено самой ЭВМ по специальной программе. При списочном задании сетевого графика упорядочение производится вручную до записи информации на машинные носители. Для [c.6]
Во многих случаях проекты, входящие в программу развития отрасли, зависимы между собой в том смысле, что для начала проекта необходимо, чтобы были завершены другие проекты. Такие зависимости удобно задавать в виде сетевого графика (графа), вершины которого [c.55]
Для расчета коэффициента напряженности работ надо построить список всех полных путей сетевого графика. Для этого используется специальный алгоритм, основанный на преобразовании сетевого графика в многоуровневый граф типа дерева , но с повторяющимися вершинами. При построении дерева сетевого графика можно использовать таблицу длительностей работ. [c.33]
Поскольку в сетевых графиках моделей типа АоА вершины соответствуют событиям, постольку эти элементы структуры обладают свойством сшивания предыдущих работ с последующими. Иными словами, любое событие наступает только тогда, когда закончены все предшествующие ему работы. С другой стороны, оно является предпосылкой для начала следующих за ним работ. Событие не имеет продолжительности и наступает мгновенно. В связи с этим предъявляются особые требования к его определению. [c.110]
Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного. рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально. [c.114]
После построения сетевого графика нумеруют его вершины. Нумерацию, при которой номер начала любой дуги меньше номера ее конца, называют правильной. [c.276]
Критическое время и критический путь. Ранний срок наступления конечного события называется критическим временем и обозначается 7 . Весь проект не может быть завершен раньше момента времени Ткр( V. е. критическое время т— это минимальный срок окончания всего комплекса работ. На сетевом графике Ткр — это длина пути наибольшей длины из начальной вершины в конечную. [c.277]
Резервы времени удобно рассчитывать по сетевому графику, так как величины Tf, Tf записаны в его вершинах. Полученные значения резервов записывают около соответствующих дуг сетевого графика. Сначала ставят полный резерв, а затем свободный. [c.280]
Сети типа "вершины-события". На рис. 5.2.10. показана сеть типа "вершины-события" после прямого и обратного прохода. Также можно рассчитывать сетевой график известными методами и в табличной форме (табл.1). [c.233]
Особое внимание при построении сетевой модели обращается на нумерацию событий (вершин графика). При нумерации событий обычно руководствуются следующими основными правилами [c.77]
Следует также отметить, что главным математическим аппаратом сетевого анализа является такой раздел дискретной математики, как теория графов. Каждая операция (функция, объект и т. п.) в структуре деятельности может быть представлена как вершина графа, а объединяющая их взаимосвязь (отношение) — как ребро графа. В качестве вершин графа могут выступать в принципе любые элементы изучаемой деятельности, характер связывающих их отношений также может быть самым разным время, расстояние, частота (вероятность), стоимость (ресурсоемкость), приоритетность и др. Таким образом, сетевой анализ открывает широчайшие возможности для оценки и моделирования поведения системы, в том числе и во временном аспекте. Используемые в сетевом анализе данные (операции и отношения между ними) могут быть представлены самым различным способом в виде графов, графиков, таблиц, матриц. [c.121]
Параметры раннего и позднего времени наступления события используются в маркировке вершин сетевого графика модели типа АоА. В левый сегмент записывается раннее время наступления соответствующего события (ЕЕТ), а в правый — позднее (LElp, что показано на рис 4. [c.113]
Чаще других используют сетевые графики, в / работе которых соответствует вершина графа (Node), а связям работ — его дуги (Arrow). Графы такого типа относят к типу "работа-вершина." [c.23]
Ограничением метода критического пути, описанного ниже, является невозможность его использования в случаях, когда сетевой график проекта содержит хотя бы один контур или петлю (Loop) — путь, проходящий через любую вершину сети более одного раза. [c.23]
КОНТУР [ losed ir uit] — термин теории графов замкнутый путь, исходящий из некоторой вершины графа и возвращающийся в нее же. При разработке сетевых графиков необходимо тщательно следить за тем, чтобы К. не возникали, ибо это означало бы, что некоторые работы следуют... после самих себя. В сложных сетях поиск К. приходится производить с использованием компьютера. Избавление от них осуществляется путем пересмотра списка работ и логических связей между ними. [c.152]
Алгоритм составления топологии многовариантной сети не отличается от известного алгоритма составления топологии сетевого графика, у которого вершины (кружки) интерпретируют работы. Каждый кружок сопряженного мультиграфа разделен на четыре сектора. Верхний сектор служит для шифра элемента, нижний — для его параметра, правый — для оптимальной нарастающей длины пути, предшествующего элементу, левый — для того же пути с учетом параметра элемента. [c.315]
Сетевая диаграмма (сеть, сетевой график, PERT-диаграмма) -графическое отображение работ проекта и их взаимосвязей. В планировании и управлении проектами под термином сеть понимается полный комплекс работ и событий проекта с установленными между ними зависимостями. Сетевая диаграмма не является блок-схемой в том смысле, в котором это средство используется для моделирования деловых процессов. Принципиальным отличием ее от блок-схемы является то, что сетевая диаграмма моделирует только логические зависимости между элементарными работами. Она не отображает входы, процессы и выходы и не допускает повторяющихся циклов, или петель. Сетевые диаграммы отображают сетевую модель в графическом виде как множество вершин, соответствующих работам связанных линиями, представляющими взаимосвязи между работами. Этот граф называется сетью типа вершина -работа , или диаграммой предшествования. [c.463]
Пример3.5. Пусть сетевой график из четырех проектов имеет вид, показанный на рис. 3.4. В вершинах указаны номера проектов (верхнее [c.56]
