Решение общей проблемы в одной экономико-математической модели сформулировать невозможно, так как для каждой ступени возникает многоэтапная задача размещения с нелинейной функцией цели и нелинейными ограничениями. [c.39]
| Рис. О.З. Линейные и нелинейные ограничения | 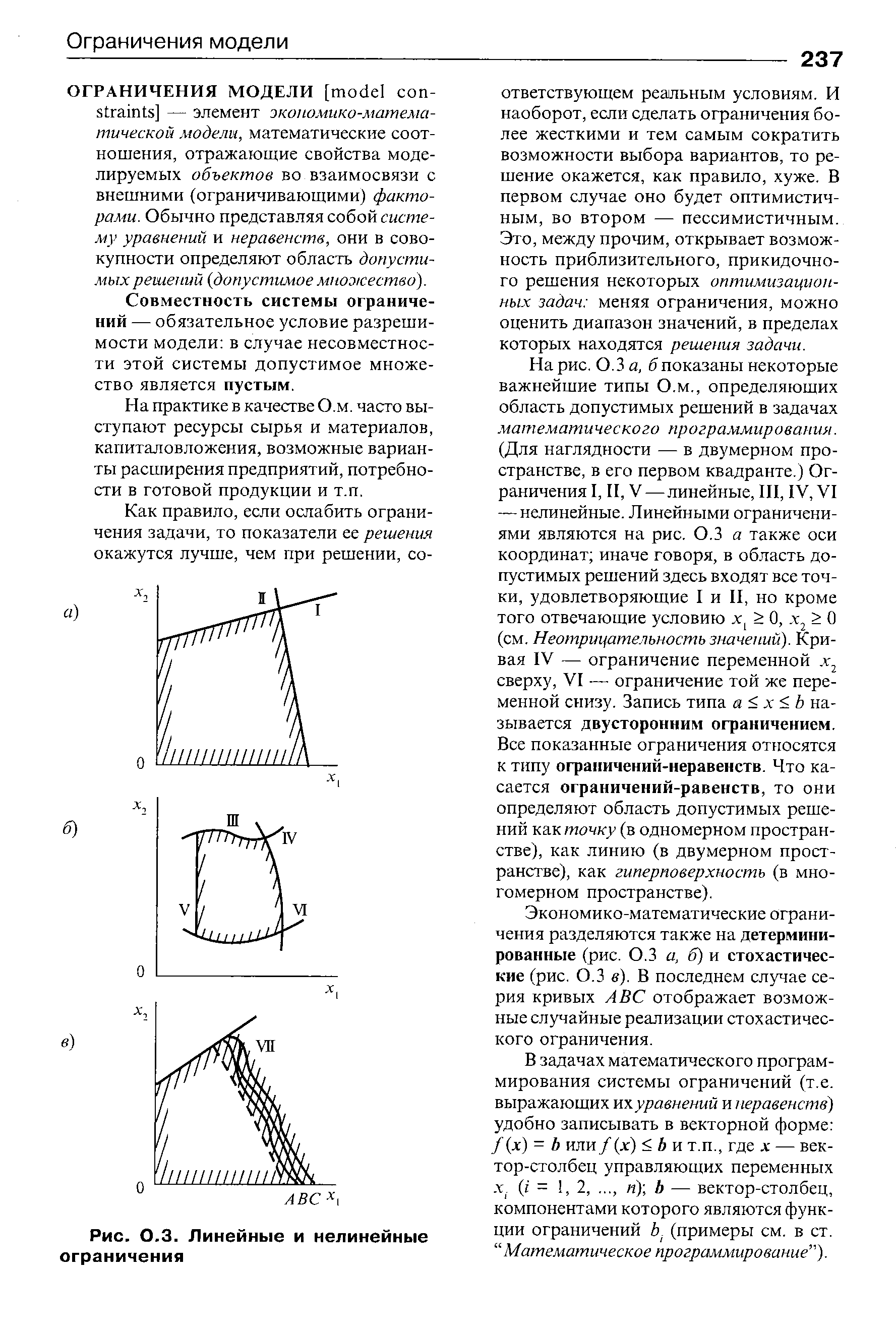 |
Нелинейное программирование охватывает методы для определения экстремума нелинейной функции в области нелинейных ограничений. [c.144]
Рассмотрим модификацию модели ОДМ, представленную в виде задачи математического программирования с нелинейными ограничениями-равенствами [c.140]
Если в задачах линейного программирования точка экстремума является вершиной многогранника, то в задачах нелинейного программирования она может лежать в вершине многогранника, на ребре (грани) или внутри области. Если задача содержит нелинейные ограничения, то область допустимых решений не является выпуклой и кроме глобального оптимума могут существовать точки локального оптимума. [c.347]
Прежде всего, для того, чтобы лучше понять, в чем же выражается неприятный эффект нелинейности, проведем сравнение задач линейного и нелинейного программирования. Начнем с множества допустимых планов. В задачах линейного программирования оно выпуклое, с конечным числом крайних точек (напоминаем, что крайней точкой называется всякая точка множества, которая не является внутренней ни для какого отрезка, целиком принадлежащего этому множеству). Это сразу становится понятным, если вспомнить, что границами множества служат гиперплоскости. В задачах же нелинейного программирования (в том случае, когда нелинейны ограничения) множество допустимых планов может быть невыпуклым, может иметь бесконечное число крайних точек. Например, пусть допустимая область на плоскости ХОУ определяется такими ограничениями [c.72]
Если (D> /) является задачей выпуклого программирования с решением х, ее целевая функция f(x) и функции ограничений g x) — дифференцируемы, нелинейные ограничения в форме неравенств удовлетворяют условию регулярности Слейтера, то существует такой вектор и > 0, что (х,и) — седловая точка функции Лагранжа Ф(х,и). [c.105]
Предположим, что нулевая гипотеза состоит из системы q нелинейных ограничений на вектор коэффициентов ft. Пусть дана линейная модель у = Х/3 + и при стандартном условии на распределение вектора ошибок и JV(0, 1(0)). Запишем ограничения в виде [c.258]
Общего способа решения задачи (4.25) не существует в силу нелинейности ограничения на риск. Целесообразно для решения задачи оптимизации вида (4.25) [c.91]
Уже из описания данной модели видна ограниченность ее применения в строительстве. Далее будет показана необходимость использования в трубопроводном строительстве более сложных нелинейных экономико-математических моделей оптимального планирования. [c.25]
Таким образом, целевая функция (2.9) вместе с ограничениями (2.11), (2.17) и (2.18) представляет собой экономико-математическую модель задачи необходимо найти такие значения темпов выполнения работ сетевой операционной модели (количества добавляемых на процессы технологических звеньев), которые обеспечивают строительство объекта в плановые сроки при минимуме затрат на передислокацию строительно-монтажных подразделений. Данная задача относится к классу нелинейных задач целочисленного программирования. Даже в упрощенном варианте организации строительства без учета сменности работ решение задачи представляет определенную трудность. [c.50]
Зависимость отдельных составляющих целевой функции от числа пунктов разгрузки, включенных в какой-либо вариант внешнего транспортного обеспечения и условно рассматриваемых как непрерывные функции в области целочисленных величин числа пунктов разгрузки пгв, представлена на рис. 27. Как видно из рисунка, с увеличением числа пунктов разгрузки возрастают суммарные затраты на их организацию и уменьшаются транспортные расходы по доставке труб к месту работ. Следовательно, целевая функция как сумма указанных составляющих имеет экстремум при некотором значении числа пунктов разгрузки. Учитывая нелинейную зависимость функционала и его отдельных составляющих от числа вводимых пунктов разгрузки и искомых переменных, для решения поставленной задачи не могут быть применены классические методы математического программирования (например,. линейного). Как известно из курса высшей математики, математическое программирование — область математики, разрабатывающая теорию и методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Само название программирование взято из линейного программирования, где оно обычно обозначает распределение наилучшим образом ограниченных ресурсов для достижения поставленных целей. Следовательно, термин программирование здесь можно заменить термином планирование . [c.145]
Нелинейная модель выбора рациональной суточной производительности комплекса установок не противопоставляется и не препятствует применению известной линейной модели оптимизации производственной программы НПЗ. Она формирует лишь экономически обоснованные ограничения на значения суточной производительности установок АВТ, КК, КР. В их пределах возможна реализация экономических возможностей оптимизации производственной программы всего шлейфа сопутствующих установок специфическими средствами линейной модели. [c.43]
Модель (3.8) — общее представление нелинейной статической модели с конечным числом ограничений. Так же, как и в случае линейных систем, модель (3.8) можно представить в виде (3.7), только теперь множество X уже не является многогранным. [c.33]
Как видим, это — довольно сложная система равенств и неравенств, причем равенства являются нелинейными (несмотря на линейность исходной задачи). Решение таких систем, особенно в случае значительного числа переменных п ограничений (а в практических задачах это число достигает сотен и тысяч), представляет собой весьма сложную проблему. Во многих случаях преодолеть возникающие здесь трудности не удается. В связи с этим использование методов математического моделирования для принятия экономических решений долгое время не имело под собой прочной вычислительной основы. Положение изменилось только после того, как были разработаны эффективные ме- [c.49]
Методы динамического программирования применяются при решении оптимизационных задач, в которых целевая функция или ограничения, или же первое и второе одновременно характеризуются нелинейными зависимостями. Признаками нелинейности является, в частности, наличие переменных, у которых показатель степени отличается от единицы, а также наличие переменной в показателе степени, под корнем, под знаком логарифма. [c.168]
От нелинейности в модели относительно Эг/-8 можно освободиться, приняв предположение, состоящее в том, что к заданному году 9/ -s о должно быть введено в разработку не более некоторой определенной части месторождения. Тогда ограничение (153) заменится парой условий [c.223]
Для нелинейной связи показатель средней силы связи не имеет значения (или имеет ограниченное значение). [c.128]
Практическое значение ее в том, что есть системы, в которых среди всех факторов, влияющих на результативный признак, выделяется один важнейший фактор, который в основном определяет вариацию результативного признака. Измерение парных корреляций составляет необходимый этап в изучении сложных, многофакторных связей. Есть такие системы связей, при изучении которых следует предпочесть парную корреляцию. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связей для выполнения расчетов преобразуются в линейную форму. [c.238]
При решении задачи можно выбрать метод экстраполяции оценок переменных для каждого шага поиска — линейная или квадратичная (для задач с нелинейной целевой функцией), метод численного дифференцирования для целевой функции — прямые или центральные разности (для задач с нелинейной целевой функцией), метод поиска — метод Ньютона (требуется много оперативной памяти) или метод сопряженных градиентов (больше итераций). Основным ограничением модели является максимальное число переменных — 200. Несколько оптимизационных моделей на одном листе можно сохранять и загружать по мере необходимости. [c.457]
Существуют различные подходы к использованию сетевых оптимизационных моделей верхнего уровня для анализа адаптивных характеристик перспективных планов. Один из них заключается в учете адаптивных характеристик перспективного плана как дополнительных ресурсных ограничений. В принципе такой подход может быть реализован и при использовании несетевых оптимизационных моделей отраслевого планирования линейных, нелинейных, целочисленных. [c.43]
Экономико-математическое моделирование базируется на построении различных моделей. Экономико-математическая модель — это определенная схема развития рынка ценных бумаг при заданных условиях и обстоятельствах. При прогнозировании используют различные модели (однопродуктовые и многопродуктовые, статистические и динамические, натурально-стоимостные, микро- и макроэкономические, линейные и нелинейные, глобальные и локальные, отраслевые и территориальные, дескриптивные и оптимизационные). Наибольшее значение в прогнозировании имеют оптимизационные модели (модели экстремума). Оптимизационные (или оптимальные) модели представляют собой систему уравнений, которая-кроме ограничений (условий) включает также особого рода уравнение, называемое функционалом, или критерием оптимальности. С помощью такого критерия находят решение, наилучшее по какому-либо показателю. [c.263]
При линейных ограничениях выбор показателя качества идентификации в виде положительно определенной квадратичной формы (6.14) вполне оправдан. Модели квадратичного стохастического программирования поддаются конструктивному анализу. Учет нелинейных ограничений вида (6.15)-—(6.17) приводит к евылуклой и несвязной области допустимых планов. Исследование задач с. такими ограничениями связано с большими вычислительными трудностями независимо от выбора целевого функционала. В таких задачах выбор критерия качества иденти- фикации определяется главным образом содержательными соображениями. Трудности, связанные с упрощением вычислительной процедуры, отходят здесь на второй план. [c.49]
Структурное соответствие производства и потребления как важный компонент рыночного равновесия на современном этапе выражается, прежде всего, в адекватности качественной структуры нефтепродуктов условиям их потребления и экономическим интересам производителей. Такая гармония достигается при оптимальном уровне качества, который является ориентиром в технической политике. Если оценить с этой позиции существующие методические средства, то они оказываются непригодными для решения данной задачи. По своему назначению таковым должен бы быть комплексный показатель уровня качества нефтепродуктов. Однако проведенный ранее анализ применяемых на практике методов его расчета, рекомендованных стандартами, обнаружил ограниченность аналитических свойств комплексного показателя. Как было показано в п.п. 3.5., даже нелинейные формы (3.14), (3.24) предполагают однонаправленность изменения полезности продукции при повышении (или снижении) значений единичных показателей уровня качества. [c.80]
Заметим, что на сети, изображенной на рис. 16, груз из пункта / может быть перевезен в пункт IX по разным дорогам. Если бы мы захотели перейти к матричной форме транспортной задачи, то нам надо было бы заранее решить, по какому из маршрутов мы повезем груз. Если пропускная способность каждой из дорог не ограничена, то переход к матричной форме не вызовет затруднений при относительно простой сети. В более сложных сетях этот вопрос можно решить с помощью специально предназначенных для этого алгоритмов. Если же пропускная способность некоторых участков сети дорог ограничена, то возникают осложнения следующего рода. Пусть по участку дороги от пункта IV до пункта V можно провезти не более 30 единиц груза. Но по этой дороге мы можем везти груз и из пункта / в пункты V, VIII и IX, и из пункта /// в пункт VI. Спрашивается, на какие из перевозок мы должны наложить ограничения при переходе к матричной постановке По-видимому, на все вместе. Но, с другой стороны, если возможности дороги между пунктами IV и V будут исчерпаны, часть грузов можно будет перевозить по другим дорогам. Однако при этом изменится величина затрат на перевозки единицы груза, так что в матричной постановке величина сц оказывается зависимой от ху, и задача становится нелинейной. Хотя все эти трудности перехода к матричной постановке задачи перевозки грузов все-таки можно преодолеть при помощи разнообразных искусственных приемов, многие предпочитают решать задачи в сетевой постановке, не переходя к матричной. Алгоритмы решения транспортной задачи были преобразованы к форме, пригодной для решения задач сразу на сети. К сожалению, эти алгоритмы более громоздки, чем алгоритмы решения транспортной задачи в матричной постановке. Есть и другие недостатки сетевой постановки задачи, есть и ряд дополнительных преимуществ, [c.160]
При фиксированном значении 0/ -s условия (151) — (158) определяют линейные ограничения, и задача становится нелинейной только относительно функционала. В этом случае, если возможно сведение полученной модели к решению известного типа задач математического программирования, появляется метод решения и исходной задачи (т. е. нелинейной относительно 6 /s). Для этого достаточно найти оптимальные планы группы задач, в которых фиксиро- [c.222]
