Экономико-математические методы должны также широко применяться при определении мест размещения и оптимальной мощности перевалочных нефтебаз. Эту задачу можно отнести к многоступенчатой задаче целочисленного программирования, состоящей из нескольких звеньев. С одной стороны, здесь должны быть учтены добыча нефти и ее транспорт к потребителям, с другой стороны, транспорт и хранение нефтепродуктов при их продвижении от НПЗ к потребителям. [c.82]
При наличии ограничений на ресурсы (финансовых, производственных мощностей, трудовых и т. д.), которые доступны предприятию, задача выбора набора проектов, которые приносят наибольший доход, может быть решена методами математического программирования и в самой общей постановке может быть сведена к задаче целочисленного программирования [2]. Когда денежные потоки проектов и другие параметры проектов не меняются в зависимости от принятия или отказа от проектов из рассматриваемого набора, задача может быть сведена к задаче целочисленного линейного программирования. Этот случай является практически наиболее важным. Формулировка задачи выбора оптимального набора проекта в линейном случае выглядит следующим образом [35]. Необходимо найти максимум функции L, который имеет смысл ЧТС от реализации предприятием оптимального набора проектов [c.79]
В задачах целочисленного программирования неизвестные могут принимать только целочисленные значения. [c.104]
В ряде случаев задачу целочисленного программирования решают следующим образом как непрерывную задачу линейного программирования округляют переменные проверяют допустимость округленного решения если решение допустимо, то оно принимается как целочисленное. [c.126]
К такому виду может быть легко сведена любая задача целочисленного программирования. [c.188]
Нахождение точек излома функции менее всего поддается механизации расчета. Это в значительной мере объясняется тем, что потребное количество рабочих при каждом ритме определяется одновременно с закреплением рабочих за операциями. Задача же закрепления операций за рабочими в общем случае может быть сформулирована как задача целочисленного программирования, решение которой связано. со значительными трудностями. [c.78]
Таким образом, данная задача принадлежит к классу экономико-математических задач целочисленного программирования с значительным числом вариантов. Например, если число работ равно 20, а на каждую работу может добавлено всего одно технологическое звено при односменной организации работ, то число вариантов решения этой простейшей сетевой модели составляет более 1 миллиона. [c.102]
Названные выше разнообразные дисциплины отличаются друг от друга видом целевой функции fix) и области М. Напр., если fix) линейна, а М— выпуклый многогранник, имеем задачу линейного программирования если же дополнительно ставится условие, чтобы переменные были целочисленными, то имеем задачу целочисленного программирования если зависимость U отд (т.е. форма f) носит нелинейный характер, то задачу нелинейного программирования. [c.187]
Методы решения задач целочисленного программирования. Расскажем о двух методах решения задач. В соответствии с методом приближения непрерывными задачами сначала решается задача линейного программирования без учета целочисленности, а затем в окрестности оптимального решения ищутся целочисленные точки. [c.177]
Для каждой конкретной задачи целочисленного программирования (другими словами, дискретной оптимизации) метод ветвей и границ реализуется по-своему. Есть много модификаций этого метода. [c.177]
Решите задачу целочисленного программирования [c.184]
Задачи целочисленного программирования [c.464]
Точные методы решения задач целочисленного программирования можно классифицировать как методы отсечений и комбинаторные методы. [c.466]
Сформулируем задачу целочисленного программирования с булевыми переменными. [c.497]
Сформулируем соответствующую задачу целочисленного программирования. [c.500]
Решите следующие задачи целочисленного программирования [c.532]
| Рис. 13.1. Геометрическая интерпретация решения задачи целочисленного программирования | 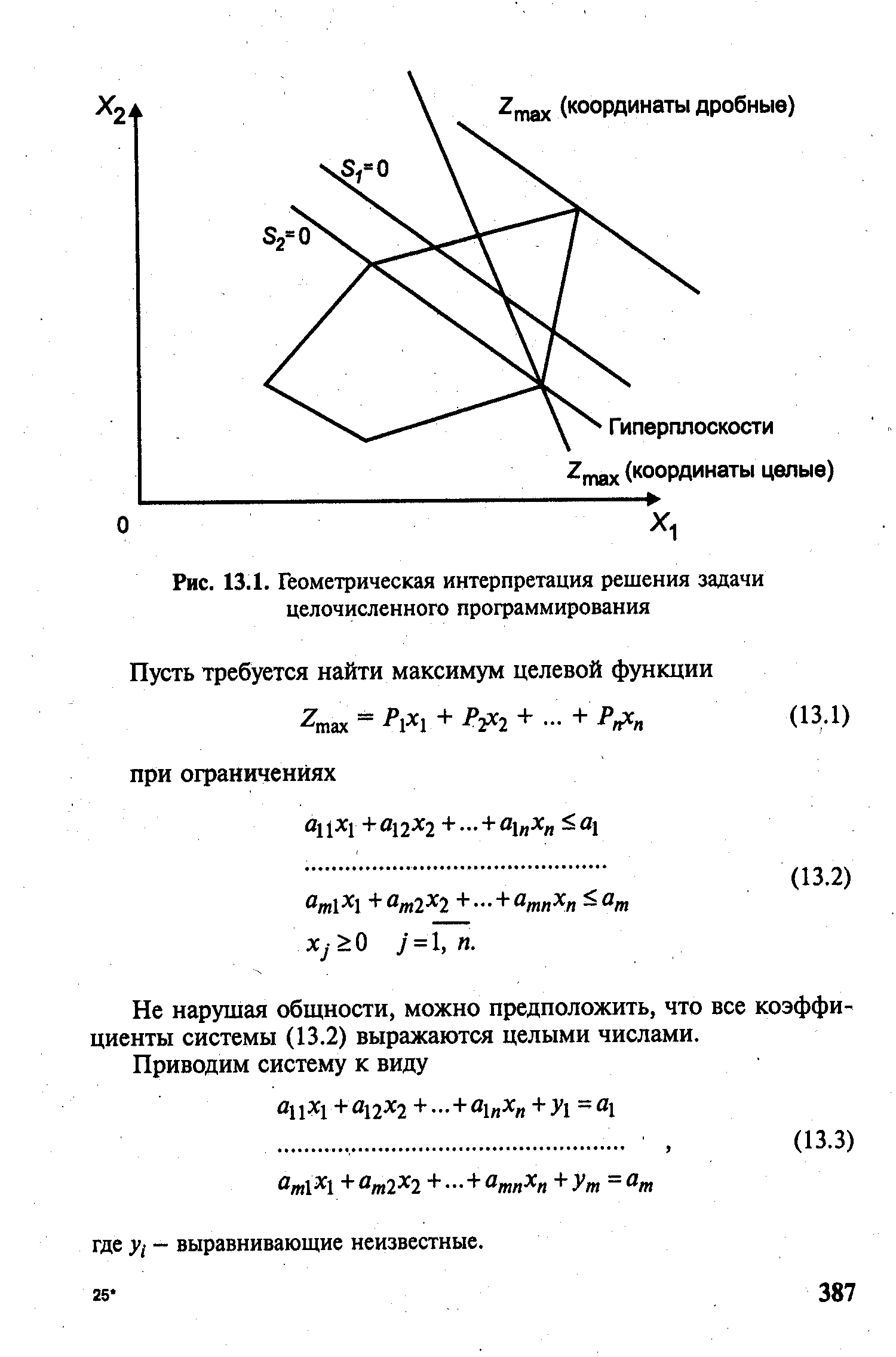 |
При решении практических вопросов особенно часто возникают такие задачи целочисленного программирования, в которых переменные принимают лишь два значения нуль и единица. Экономически это означает, что то или иное возможное решение принимается или отвергается Например, строить или не строить домну, приобретать или не приобретать машину и т. п. [c.109]
Задачи, в которых имеются ограничения типа (4) или сводящиеся к ним, получили название задач целочисленного программирования. Их отличает от линейно-программных моделей, казалось бы, сущий пустяк — добавление условия (4). Но из-за такого пустяка при решении подобных задач возникают большие трудности. Дело в том, что оптимальное решение в этом случае не обязательно находится в одной из вершин многогранника, задаваемого условиями (1) — (3), и обычные методы линейного программирования, использующие это обстоятельство, оказываются бессильными при решении задач целочисленного программирования. [c.110]
Так как задача целочисленного программирования отличается от обычной задачи линейного программирования только условием (4), то естественно попытаться хоть как-нибудь использовать для ее решения хорошо разработанный аппарат линейного программирования. Так и поступим. Решим задачу линейного программирования без условия (4). Если окажется, что в оптимальном плане величины xi принимают целочисленные значения, то исходная задача решена — условие (4) выполнилось автоматически. [c.110]
Сравнительно легко показать, что всякий оптимальный опорный план задачи линейного программирования, рассматриваемой на множестве R, является также оптимальным опорным планом той же задачи, но рассматриваемой на дискретном множестве R. Исходя из этого утверждения вроде бы можно предложить такой способ решения задачи целочисленного программирования а) определить множество R целых точек многоугольника ограничений Q б) образовать его линейную выпуклую оболочку R в) на множестве R решить задачу линейного программирования без условия целочисленности. Полученное решение и будет являться решением поставленной задачи. [c.111]
Поэтому для решения задач целочисленного программирования нередко применяются методы комбинаторного анализа. Остановимся здесь на одном из них — методе ветвей и границ. Изложим его применительно к общей задаче дискретного программирования. [c.113]
В каждом из перечисленных направлений оптимального программирования в свою очередь могут возникать задачи, требующие специальных методов решений. К числу таких задач относятся задачи, в которых исходные условия либо могут быть заданы несколькими дискретными значениями — задачи целочисленного программирования, либо исходные условия изменяются в определенных пределах — параметрическое программирование. [c.165]
Формирование оптимальной инвестиционной программы с учетом риска и бюджетного ограничения сводится к задаче линейного целочисленного программирования с булевыми переменными. [c.182]
Решение задачи осуществляется методами линейного целочисленного программирования. Однако сложность заключается в том, [c.182]
Линейное программирование позволяет глубоко проанализировать задачу, и все же оно предполагает те же пять допущений, о которых говорилось выше при обсуждении метода анализа вклада в расчете на единицу ограничивающего фактора, а именно наличие определенности линейность функции затрат линейность функции выручки равенство объема реализации объему выпуска и независимость продуктов. Кроме того, мы предположили, что продукты делимы, т.е. можно произвести и продать нецелое их количество, что не всегда соответствует действительности. (Это предположение в неявной форме было присуще и методике анализа вклада/релевантных затрат на единицу ограничивающего фактора.) Данные недостатки преодолеваются в более совершенных методах анализа, например, в нелинейном или целочисленном программировании. Но даже и такие методы не полностью гарантируют точность результатов, а их чрезмерная сложность может помешать их пониманию и эффективному использованию. [c.376]
При решении задачи целочисленного линейного программирования используются специальные методы, которые широко известны и описаны в литературе [2]. [c.80]
При большом числе проектов п, процесс решения задач целочисленного линейного программирования является трудоемким, требует больших затрат времени и использования специальных программных средств. [c.81]
Обычно управленческие решения принимаются в одной из двух возможных ситуаций или в условиях относительной определенности, или в условиях крайней неопределенности. В табл. 16.1 схематично представлены модели, сгруппированные по степени сложности и характеру переменных решаемых задач. Обычно количественная оценка принятия решений в условиях относительной определенности сводится к максимизации или минимизации некоторых целей (например, к максимизации прибыли и минимизации рисков), и при этом лицо, принимающее решение, должно рассмотреть и возможные ограничения (например, ограничения производственных мощностей или финансовых ресурсов), которые усложняют достижение намеченных целей. Модели линейного и целочисленного программирования поэтому являются наиболее распространенными способами решения масштабных задач такого бизнеса. В этих моделях используются математические методы для определения максимальных или минимальных значений какого-то объективного результата, зависящего от комплекса некоторых субъективных ограничений. [c.254]
Сложные управленческие задачи Линейное и целочисленное программирование Анализ моделей принимаемых решений [c.254]
Линейное и целочисленное программирование используется для принятия управленческих решений в таких областях, как планирование и составление графиков производства, создание и расходование складских запасов, финансовое планирование, отбор портфеля заказов, маркетинг и реклама товаров компаний и т. п. Тем не менее при всей своей прогностической способности линейное и целочисленное программирование не отличается высокой степенью предвидения элементов неоднозначности. Уже давно концептуально решена задача оптимизации поставленной цели, зависящей от ряда ограничительных факторов. Интуиция и здравый смысл являются серьезными помощниками при решении довольно простых задач и позволяют оптимизировать результат решения задачи без специальных знаний и сложных методик количественной оценки. Однако при решении сложных задач, включающих сотни переменных и ограничителей, интуиция и здравый смысл помогают мало. [c.254]
ГОМОРИ СПОСОБ [Gomory method] — прием, с помощью которого достигается решение линейной задачи целочисленного программирования. Разработан американским математиком Р. Гомори. Состоит в автоматическом введении дополнительных ограничений, приводящих через конечное количество шагов к новой линейной задаче с целочисленным/решением, которое оказывается одновременно оптимальным целочисленным решением исходной задачи (если только она имеет решение). См. также Дискретное программирование. [c.64]
Вычисление медианы Кемени является задачей целочисленного программирования. Для ее нахождения используют различные алгоритмы дискретной математики, в частности, основанные на методе ветвей и границ. Применяют также алгоритмы, основанные на идее случайного поиска, поскольку для каждого бинарного отношения нетрудно найти множество его соседей. [c.335]
Существует эвристический подход к решению задач целочисленного программирования (ЗЦП), основанный на решении ЗЦП как задачи Л П. Использование процедур округления нецелочисленного оптимального решения задачи ЛП дает возможность пблучать приближенное оптимальное целочисленное решение. Например, если в оптимальном решении двумерной задачи ЛП значения переменных х и Xi оказались равными 3,5 и 4,4 соответственно, то в качестве кандидатов на роль приближенного целочисленного оптимального решения необходимо рассмотреть точки (3 4), (4 4), (4 5), (3 5), полученные в результате округления. Заметим, однако, что истинное оптимальное целочисленное решение может не совпадать ни с одним из четырех, указанных выше. [c.465]
Перейдем теперь к частному случаю задач целочисленного программирования. В этом частном случае искомая переменная xj в результате решения может принимать не любое целое значение, а только одно из двух либо 0, либо 1. Чтобы такие переменные отличать от обычных, будем их обозначать чбрез 8у. [c.493]
Следует отметить, что если алгоритм ближайшего непосещенного города никогда не даст возможности построить оптимальный маршрут, то алгоритм двух вертолетов, упрощенное описание которого мы рассмотрели, дает либо оптимальное решение, либо существенно лучшее (по сравнению с алгоритмом ближайшего непосещенного города ). То, что данный алгоритм не всегда дает оптимальное решение, объясняется просто в данном случае имеет место задача целочисленного программирования с тупиковыми локальными оптимумами. Однако петли маршрута легко обнаруживаются визуально на экране монитора, поэтому неоптимальные участки легко корректируются вручную. [c.237]
Решения модели перераспределения ресурсов с требованием целочисленности переменных и линейным критерием относятся к задаче целочисленного программирования. К ним можно применить следующие методы оптимизации метод отсекающих плоскостей (метод Гомори), различные методы построения ослабленных задач, метод ветвей и границ и различные его модификации, например метод штрафных функций. [c.183]
Г. М. М а к а ц, Б. А. М а к е е в. Оптимизатор для решения некоторых задач целочисленного программирования.— Автом. и телемех., 1964, 25, 2. [c.238]
Смотреть страницы где упоминается термин Задачи целочисленного программирования
: [c.148] [c.79] [c.499] [c.369] [c.519] [c.189] [c.179]Смотреть главы в:
Производственный менеджмент -> Задачи целочисленного программирования
